Unidad 4 Cadenas de Markov de Tiempo Contínuo
En esta unidad, consideramos un sistema estocástico que se observa continuamente a lo largo del tiempo, siendo \(X_t\) el estado en el momento \(t\), con \(t \geq 0\). Siguiendo la definición de las CMTD, a continuación definimos las cadenas de Markov de tiempo continuo (CMTC).
Definición 4.1 Un proceso estocástico \(\{X_t; t \geq 0\}\) con espacio de estados \(S\) es una cadena de Markov de tiempo continuo, CMTC, si para todo \(i\) y \(j\) en \(S\), y \(t, s \geq 0\), cumple la propiedad de Markov:
\[P(X_{s+t} = j \mid X_s = i, X_u, 0 \leq u \leq s) = P(X_{s+t} = j \mid X_s = i).\]
La CMTC \(\{X_t; t \geq 0\}\) se denomina homogénea si el cambio entre dos instantes cualesquiera depende exclusivamente del tiempo transcurrido, esto es para cualquier \(t, s \geq 0\),
\[P(X_{s+t} = j \mid X_s = i) = P(X_t = j \mid X_0 = i).\]
En toda esta unidad asumimos que las CMTC con las que trabajamos son homogéneas y tienen espacio de estados finito \(S=\{1, 2,,...,N\}\) de forma que podemos definir la probabilidad de pasar del estado \(i\) al estado \(j\) en un periodo de amplitud \(t, (0,t],\) como:
\[p_{ij}(t) = P(X_t = j \mid X_0 = i), \quad 1 \leq i, j \leq N.\]
La matriz de probabilidad de transición \(P(t)\) de una CMTC \(\{X_t; t \geq 0\}\) viene dada por las distribuciones de probabilidad condicionadas (por filas) de pasar de un estado \(i\) a un estado \(j\) en un periodo de tiempo de amplitud \(t\):
\[P(t) = \begin{pmatrix} p_{11}(t) & p_{12}(t) & ... & p_{1N}(t)\\ p_{21}(t) & p_{22}(t) & ... & p_{2N}(t)\\ ... & ... & ... & ...\\ p_{N1}(t) & p_{N2}(t) & ... & p_{NN}(t) \end{pmatrix}\]
Dicha matriz de transición verifica que:
- Todos sus elementos son probabilidades condicionadas \(\{p_{ij}(t); j \in S\}\)
\[1 \geq p_{ij}(t) \geq 0, \quad 1 \leq i, j \leq N; t \geq 0\]
- La suma de las probabilidades en cada fila, esto es, de acceder a cualquiera de los estados a partir de un estado \(i\) es igual a 1.
\[\sum_{j=1}^N p_{ij}(t) = 1, \quad 1 \leq i, j \leq N; t \geq 0\]
- Ecuaciones de Chapman-Kolmogorov
\[p_{ij}(s+t) = \sum_{k=1}^N p_{ik}(s)p_{kj}(t) = \sum_{k=1}^N p_{ik}(t)p_{kj}(s) , \quad 1 \leq i, j \leq N; t \geq 0\]
La dificultad principal con \(P(t)\) es que resulta díficil de obtener de forma inmediata para la mayoría de las CMTC, al contrario de lo que ocurría con las CMTD. Necesitamos un método simple que nos permita describir de forma rápida el comportamiento del proceso. A continuación, sentamos las bases para el estudio de las CMTC a partir de los tiempos de permanencia en cada uno de los estados del proceso. Dado que la única distribución que verifica la propiedad de pérdida de memoria es la exponencial, la utilizaremos como base para la construcción de una CMTC.
4.1 Evolución del proceso
Sea \(X_t\) el estado de un sistema en el instante temporal \(t\). Supongamos que el espacio de estados del proceso estocástico \(\{X_t; t \geq 0\}\) es \(S=\{1, 2,...,N\}\). La evolución aleatoria del sistema se produce de la siguiente manera:
Supongamos que el sistema comienza en el estado \(i\) y permanece allí durante un tiempo \(Exp(r_i)\) que denominamos tiempo de permanencia en el estado \(i\), con \(r_i\) la tasa media de permanencia; recordemos que en la distribución exponencial las tasas medias son el recíproco de los tiempos medios.
Al final del tiempo de permanencia en el estado \(i\), el sistema realiza una transición repentina al estado \(j\) con probabilidad \(p_{ij}\), independientemente del tiempo que el sistema haya permanecido en el estado \(i\). Una vez en el estado \(j\), permanece allí durante un tiempo \(Exp(r_j)\).
A continuación pasa a un nuevo estado \(k\) con una probabilidad \(p_{jk}\), independientemente de la historia del sistema hasta el momento, y repite este comportamiento hasta que finaliza el tiempo de observación del proceso.
Conviene hacer tres observaciones con respecto al funcionamiento del sistema:
- En primer lugar, las probabilidades de salto \(p_{ij}\) no deben deben confundirse con las probabilidades de transición \(p_{ij}(t)\). En este caso, \(p_{ij}\) actúa como la probabilidad de que el sistema pase al estado \(j\) cuando sale del estado \(i\).
- En segundo lugar, \(p_{ii} = 0\), dado que, por definición, el tiempo de permanencia en el estado \(i\) es el tiempo que el sistema pasa en el estado \(i\) hasta que sale de él; por lo tanto, no es posible una transición de \(i\) a \(i\).
- En tercer lugar, en caso de que el estado \(i\) sea absorbente, es decir que el sistema permanezca en ese estado para siempre una vez que llegue a él, fijamos \(r_i = 0\).
Con estas premisas podremos obtener la matriz de probabilidades de salto, \(P\), que denotaremos como:
\[P = \begin{pmatrix} p_{11} & p_{12} & ... & p_{1N}\\ p_{21} & p_{22} & ... & p_{2N}\\ ... & ... & ... & ...\\ p_{N1} & p_{N2} & ... & p_{NN} \end{pmatrix}\]
Teorema 4.1 El proceso estocástico \(\{X_t; t \geq 0\}\) con parámetros \(r_i\), \(1 \leq i \leq N\), y probabilidades \(p_{ij}\), \(1 \leq i,j \leq N\) descrito anteriormente es una CMTC.
A continuación presentamos un par de ejemplos.
Ejemplo 4.1 Sistema de vida útil de un satélite. Supongamos que la vida útil \(T\) de un satélite de gran altitud es una variable aleatoria exponencial de tasa \(\mu\) en meses, \(Exp(\mu)\), de forma que una vez que falla sigue fallando para siempre, ya que no es posible repararlo. Consideramos el proceso \(X_t = 1\) si el satélite está operativo en el momento \(t\), y 0 en caso contrario. En esta situación \(r_0 = 0\) (porque si se estropea, se queda estropeado) y \(r_1 = \mu\) (que es el inverso del tiempo esperado de vida), pero desconocemos los valores de \(P\), aunque podremos obtener la matriz de transición calculando las probabilidades \(p_{00}(t)\) y \(p_{11}(t)\) que vienen dadas por:
\[p_{00}(t) = P(\text{satélite no está operativo en t} \mid \text{satélite no está operativo en 0}) = 1\]
\[\begin{eqnarray*} p_{01}(t) &=& P(X_t=1|X_0=0) = 0 \\ p_{10}(t) &=& P(X_t=0|X_0=1) = Pr(T \leq t) = 1- e^{-\mu t}\\ p_{11}(t) &=& P(X_t=1|X_0=1) = Pr(T >t) = e^{-\mu t} \end{eqnarray*}\]La matriz de transición viene dada pues por:
\[P(t) = \begin{pmatrix} 1 & 0\\ 1- e^{-\mu t} & e^{-\mu t} \end{pmatrix}\]
Ejemplo 4.2 Sistema del viajante. Un vendedor vive en la ciudad A y es responsable de las ciudades A, B y C. El tiempo que pasa en cada ciudad es aleatorio. Tras un estudio, se ha determinado que la cantidad de tiempo consecutivo que pasa en una ciudad cualquiera sigue una variable aleatoria con distribución exponencial, cuya media de tiempo de estancia depende de la ciudad. En su ciudad natal pasa un tiempo medio de dos semanas, en la ciudad B pasa un tiempo medio de una semana, y en la ciudad C pasa un tiempo medio de una y media. Cuando sale de la ciudad A, lanza una moneda para determinar a qué ciudad va a continuación; cuando sale de la ciudad B o C, lanza dos monedas de manera que hay un 75% de posibilidades de volver a A y un 25% de posibilidades de ir a la otra ciudad. Sea \(X_t\) una variable aleatoria que denota la ciudad en la que se encuentra el vendedor en el momento \(t\), de forma que toma el valor 0 si está en A, el valor 1 si está en B, y 2 si está en C.
El proceso \(\{X_t; t \geq 0\}\) con espacio de estados \(\{0, 1, 2\}\) es una CMTC con:
- tasas de permanecia (en semanas): \(r_0 = 1/2=0.5, r_1 = 1, r_2 = 1/1.5 =0.67\) , y
- matriz de saltos
\[P = \begin{pmatrix} 0 & 0.5 & 0.5\\ 0.75 & 0 & 0.25\\ 0.75 & 0.25 & 0 \end{pmatrix}\]
4.2 Descripción del proceso
En virtud del teorema 4.1 todas las CMTC con espacios de estado finitos que tienen tiempos de permanencia no nulos en cada estado pueden ser descritos a través de las tasas de permanencia y la matriz de saltos. En este punto detallamos este análisis e introducimos todos los conceptos necesarios para el análisis del proceso.
La tasa de transición de \(i\) a \(j\) se define como el producto de la tasa de permanencia en el estado \(i\), \(r_i\), por la probabilidad de salto al estado \(j\), \(p_{ij}\)
\[\begin{equation} r_{ij} = r_i p_{ij} \tag{4.1} \end{equation}\]De forma análoga a las CMTD, una CMTC también puede representarse gráficamente mediante un grafo dirigido cuyos nodos (o vértices) indican cada uno de los estados del proceso, y surge un arco dirigido del nodo \(i\) al nodo \(j\) si \(p_{ij} > 0\); además junto a cada arco se escribe la tasa de transición \(r_{ij} = r_i p_{ij}\). Nunca habrá arcos que empiecen y acaben en el mismo nodo porque \(p_{ii}=0\). Esta representación gráfica se denomina diagrama de tasas de la CMTC.
Podemos entender la dinámica de una CMTC visualizando una partícula que se mueve de nodo en nodo en el diagrama de tasas de la siguiente manera: permanece en el nodo \(i\) durante cierto periodo de tiempo de duración variable \(Exp(r_i)\) y luego elige uno de los arcos de salida del nodo \(i\) con probabilidades proporcionales a las tasas de los arcos, trasladándose al nodo que conecta dicho arco con el nodo origen \(i\). Este movimiento continúa para siempre. El nodo ocupado por la partícula en el instante \(t\) es el estado de la CMTC en el instante \(t\).
En esta situación resulta posible obtener los valores de \(r_i\) y \(p_{ij}\) a partir de las tasas \(r_{ij}\) dado que:
\[\begin{eqnarray} \sum_{j=1}^{N} r_{ij} &=& \sum_{j=1}^{N} r_i p_{ij} = r_i \sum_{j=1}^{N} p_{ij} = r_i \tag{4.2} \\ p_{ij} &=& \frac{r_{ij}}{r_i} \quad \text{ si } r_i \neq 0. \tag{4.3} \end{eqnarray}\]Para un mejor manejo de la información, resulta conveniente construir la matriz de tasas teniendo en cuenta que \(r_{ii} = 0\) para cualquier valor de \(i\), y por tanto la diagonal de la matriz \(R\) es siempre cero. Así tenemos que:
\[R = \begin{pmatrix} 0 & r_{12} & ... & r_{1N}\\ r_{21} & 0 & ... & r_{2N}\\ ... & ... & ... & ...\\ r_{N1} & r_{N2} & ... & 0 \end{pmatrix}\]
A partir de la matriz \(R\) se puede obtener la denominada matriz generadora \(Q\) de la CMTC, que se define como aquella que tiene por elementos \(q_{ij}\), con:
\[q_{ij} = \begin{cases} -r_i, \quad \text{ si } i = j, \\ r_{ij}, \quad \text{ si } i \neq j. \end{cases}\]
de forma que:
\[Q = R-diag(r_1,...,r_N)= \begin{pmatrix} -r_1 & r_{12} & ... & r_{1N}\\ r_{21} & -r_2 & ... & r_{2N}\\ ... & ... & ... & ...\\ r_{N1} & r_{N2} & ... & -r_N \end{pmatrix}\]
Ejemplo 4.3 Continuando con el sistema de vida útil del satélite del ejemplo 4.1, podemos establecer que \(r_0 = 0\) y \(r_1 = \mu\), con \(p_{10} = 1\) y \(p_{01}\) no definida, de forma que:
\[R = \begin{pmatrix} 0 & 0 \\ \mu & 0 \end{pmatrix} \quad \text{ y } \quad Q = \begin{pmatrix} 0 & 0 \\ \mu & -\mu \end{pmatrix}\]
En esta situación el diagrama de tasas se construye con la librería diagram:
library(diagram)
estados <- c("0", "1")
nestados <- length(estados)
M <- matrix(nrow = nestados, ncol = nestados, data = 0)
R <- as.data.frame(M)
R[[2,1]] <- "mu"
pp <- plotmat(t(R), pos = 2, curve = 0.2, name = estados,
lwd = 1, box.lwd = 2, cex.txt = 0.8,
box.type = "circle", box.prop = 0.5, arr.type = "triangle",
arr.pos = 0.55, self.cex = 0.6,
shadow.size = 0.01, prefix = "", endhead = FALSE, main = "")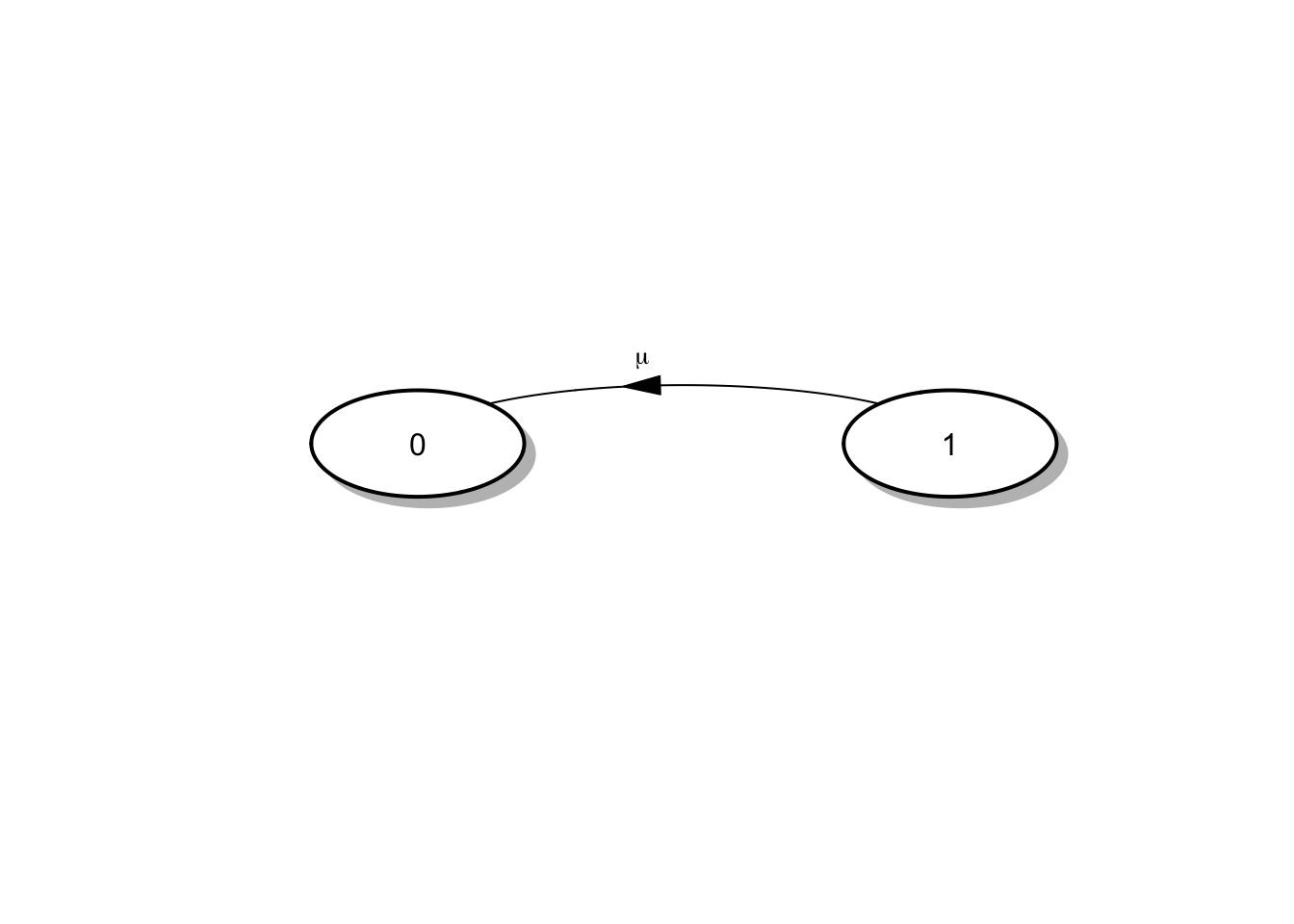
Figura 4.1: Diagrama de tasas para el tiempo de vida del Satélite
Ejemplo 4.4 Continuando con el sistema del viajante descrito en el ejemplo 4.2 ya que conocemos las tasas medias y las probabilidades de salto podemos obtener la matriz \(R\) de forma inmediata:
estados <- c("0", "1", "2")
nestados <- length(estados)
P <- matrix(nrow = nestados, ncol = nestados,
data = c(0, 0.5, 0.5, 0.75, 0, 0.25, 0.75, 0.25, 0),
byrow = 3)
r <- c(1/2, 1, 1/1.5)
R <- r*P
R## [,1] [,2] [,3]
## [1,] 0.00 0.2500000 0.25
## [2,] 0.75 0.0000000 0.25
## [3,] 0.50 0.1666667 0.00de forma que el diagrama de tasas viene dado por (asignamos el valor de la ciudad a cada uno de los posibles estados del sistema)
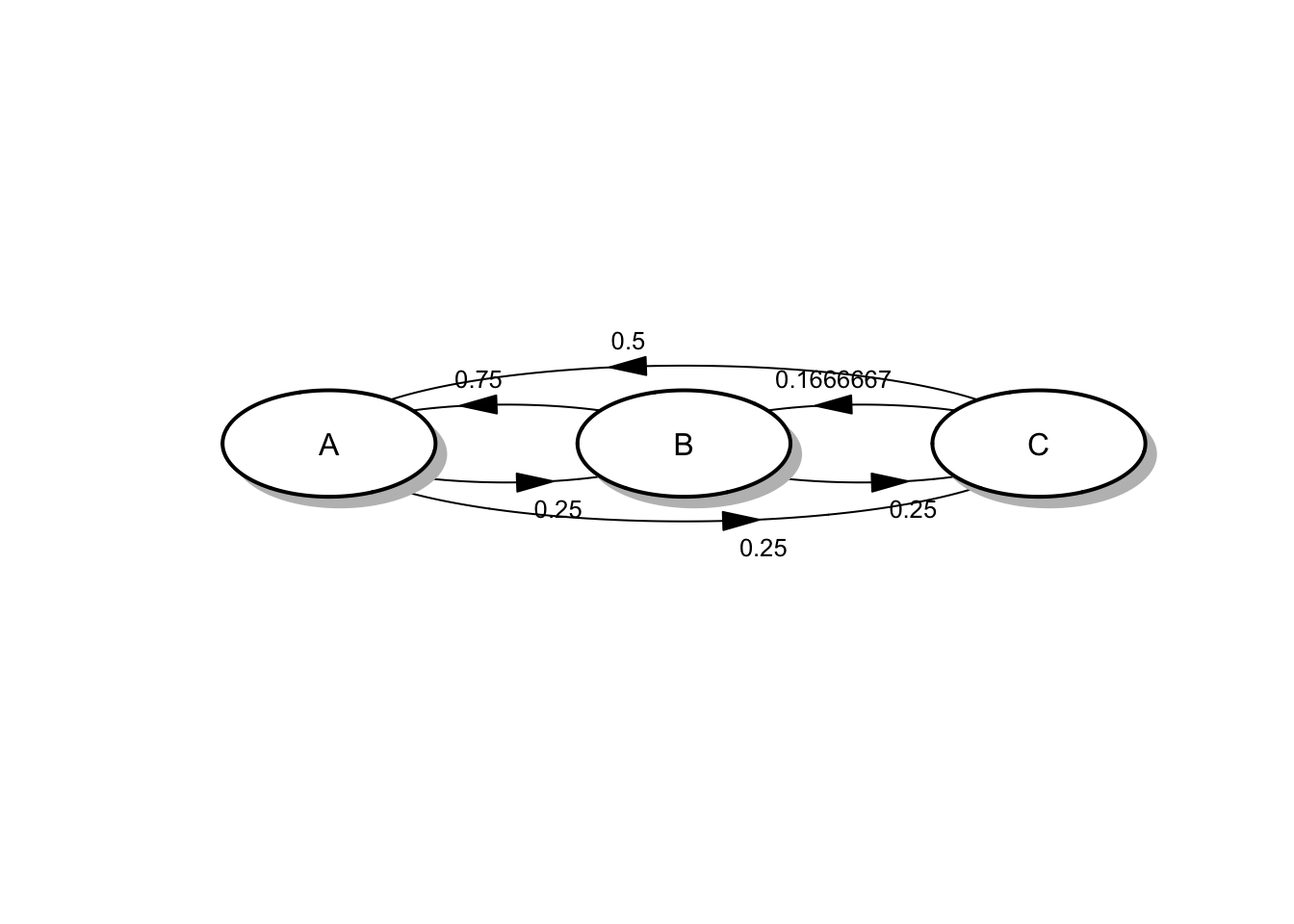
Figura 4.2: Diagrama de tasas para el proceso del vendedor
El diagrama representa el comportamiento de todo el proceso de viajes y estancias del vendedor.
Ejemplo 4.5 Sistema vida útil de una máquina. Consideramos un sistema compuesto por una máquina que funciona durante un cantidad de tiempo que viene determinada por una variable aleatoria \(Exp(\mu)\) hasta que falla. Una vez se detecta la avería, la máquina se repara. El tiempo de reparación es una variable aleatoria \(Exp(\lambda)\) y es independiente del pasado. La máquina está como nueva después de la reparación. Sea \(X_t\) el estado de la máquina en tiempo \(t\), de forma que toma el valor 1 si está en marcha y 0 si está parada (porque está siendo reparada).
En esta situación el tiempo de estancia en el estado 0 es el tiempo de reparación, de forma que \(r_0 = \lambda\), mientras que el tiempo en el estado 1 es el tiempo de funcionamiento con \(r_1 = \mu\). Además las probabilidades de salto de interés son \(p_{01} = 1\) y \(p_{10} = 1\), dado que la máquina siempre es reparada y vuelve a funcionar, y porque sabemos que la máquina debe estropearse en algún momento.
El proceso definido de esta forma \(\{X_t; t \geq 0\}\) es una CMTC cuya matriz de tasas y matriz generadora del sistema vienen dadas por:
\[R = \begin{pmatrix} 0 & \lambda \\ \mu & 0 \end{pmatrix} \quad \text{ y } \quad Q = \begin{pmatrix} -\lambda & \lambda \\ \mu & -\mu \end{pmatrix}\]
El diagrama del sistema viene dado por:
estados <- c("0", "1")
nestados <- length(estados)
M <- matrix(nrow = nestados, ncol = nestados, data = 0)
R <- as.data.frame(M)
R[[1,2]] <- "lambda"
R[[2,1]] <- "mu"
pp <- plotmat(t(R), pos = 2, curve = 0.2, name = estados,
lwd = 1, box.lwd = 2, cex.txt = 0.8,
box.type = "circle", box.prop = 0.5, arr.type = "triangle",
arr.pos = 0.55, self.cex = 0.6,
shadow.size = 0.01, prefix = "", endhead = FALSE, main = "")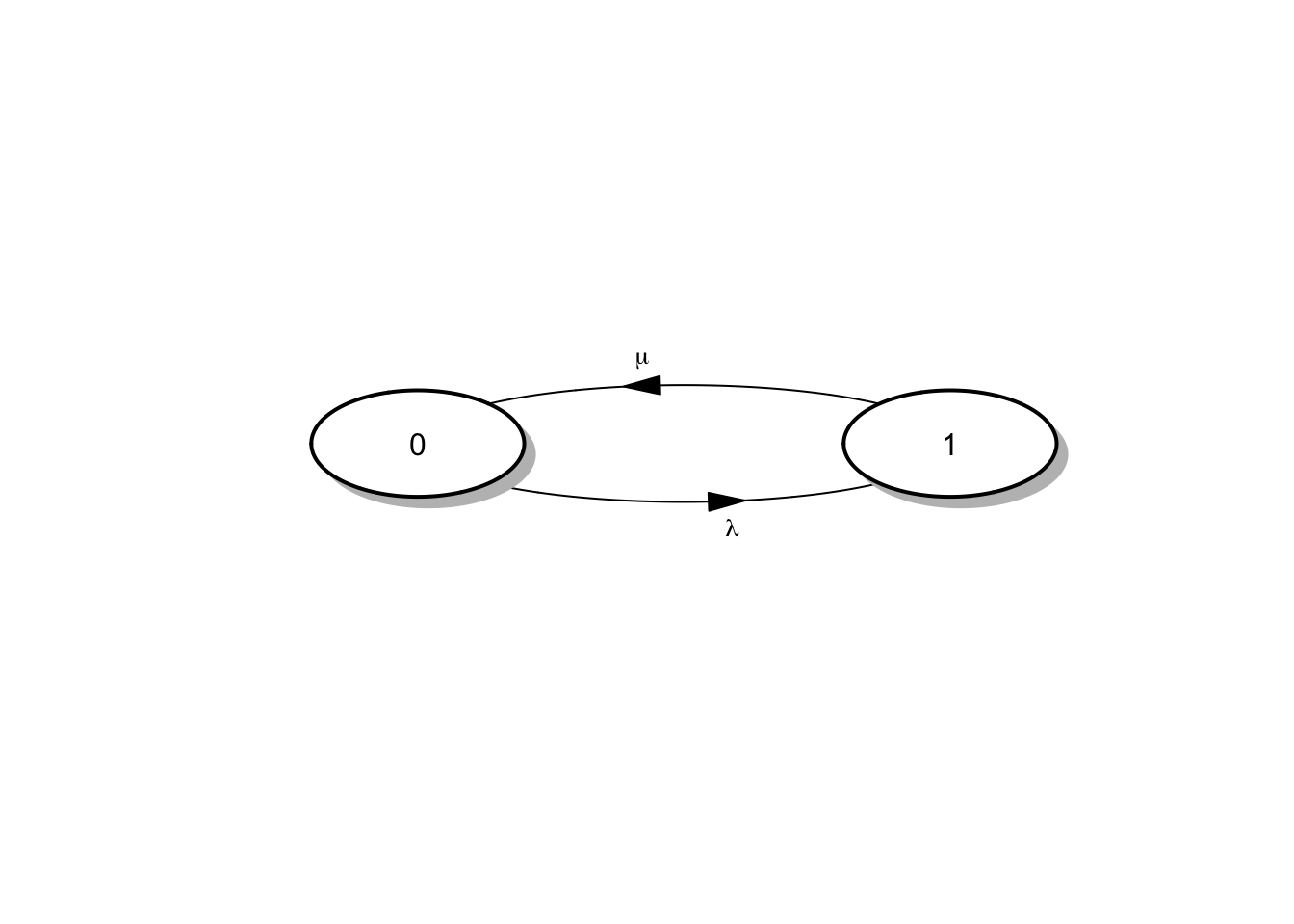
Figura 4.3: Diagrama de tasas para el sistema de una máquina
4.3 Análisis preliminar del proceso
Aunque más adelante estudiaremos los aspectos teóricos para el análisis completo de una CMTC, en este punto utilizamos la simulación del sistema para analizar su comportamiento. Nos centramos en las herramientas de simulación estudiadas hasta este punto para más adelante presentar con detalle la librería simmer que nos permite simular procesos y sistemas complejos.
Utilizamos los ejemplos 4.2 y 4.5 para mostrar cómo analizar un sistema, dado que el descrito en el ejemplo 4.1 se puede analizar sin más que describir la tasa del tiempo de vida del satélite.
4.3.1 Vida útil de una máquina
Comenzamos con el ejemplo 4.5, para el que vamos a construir un algoritmo con el que simular el sistema hasta cierto instante de tiempo.
Algoritmo para el sistema de vida útil de una máquina:
- Fijar tasas de funcionamiento \(\mu\) y reparación \(\lambda\), así como el tiempo en que el sistema estará funcionando (\(tfin\)).
- Fijar el tiempo de funcionamiento \(tfun = 0\), tiempo de reparación \(trep = 0\), y tiempo de funcionamiento del sistema \(tsis = tfun + trep\).
- Fijar el número de visitas al estado de funcionamiento \(nfun = 0\) y al estado de reparación \(nrep =0\).
Repetir los pasos siguientes hasta abandonar el sistema:
- Generar \(tfun \sim Exp(\mu)\) actualizando \(tsis\) y \(nfun\).
- Si \(tsis > tfin\), abandonar el sistema.
- Generar \(trep \sim Exp(\lambda)\) actualizando \(tsis\) y \(nrep\).
- Si \(tsis > tfin\), abandonar el sistema.
Los valores \(tfun\), \(trep\), así como las veces que se visitan los estados de funcionamiento y reparación nos permiten describir el funcionamiento del sistema para un tiempo prefijado.
Para facilitar el análisis establecemos que todos los tiempos del sistema están en días y que deseamos estudiar el sistema durante un año. Creamos una función que nos permite modificar los valores de la tasa del tiempo de funcionamiento (recíproco de la media de tiempo en funcionamiento ), la tasa de reparación (recíproco de la media del tiempo de reparación) y el tiempo total de funcionamiento del sistema. Almacenamos los resultados de cada paso por el sistema para poder realizar los análisis correspondientes.
TSIM_one_machine <- function(tasafun, tasarep, tfin)
{
# Parámetros de la función
# =========================
# tasafun: tasa de funcionamiento
# tasarep: tasa de reparación
# tfin: tiempo de funcionamiento del sistema
# inicialización de parámetros del sistema
tfun = trep = nfun = nrep = tsis = vector()
# estado inicial del sistema
i <- 1
tfun[i] = trep [i] = nfun[i] = nrep[i] = 0
tsis[i] <- tfun[i] + trep[i]
# Bucle de simulación
while(tsis[i] <= tfin)
{
i<- i + 1
# Máquina en funcionamiento
nfun[i] = nfun[i-1] + 1
tfun[i] = rexp(1, tasafun)
tsis[i] = tsis[i-1] + tfun[i]
trep[i] = 0 #Actualizamos estos dos parámetros ya que no hemos entrado en reparación
nrep[i] = nrep[i-1]
if(tsis[i] > tfin) {
# adaptamos valores para quedarnos en los 365 días
tfun[i] <- tfin - tsis[i-1]
tsis[i] <- tsis[i-1] + tfun[i]
break
}
# Máquina en reparación
nrep[i] = nrep[i-1] + 1
trep[i] = rexp(1, tasarep)
tsis[i] = tsis[i] + trep[i]
if(tsis[i] > tfin) {
# adaptamos valores para quedarnos en los 365 días
trep[i] <- tfin - tsis[i-1]
tsis[i] = tsis[i] + trep[i]
break
}
}
res <- tibble(tfun, nfun, trep, nrep,tsis)
# Devolvemos resultados del sistema quitando la fila de inicialización
return(res[-1,])
}Supongamos que a través de los registros históricos de funcionamiento y reparación de la máquina se sabe que el tiempo medio de funcionamiento es de 60 días (\(\mu = 1/60\)) y el tiempo medio de reparación es de cuatro días (\(\lambda = 1/4\)). Además se está interesado en estudiar el funcionamiento del sistema para el próximo año (365 días). Queremos pues, estimar:
- Proporción del tiempo que la máquina está funcionando y en reparación.
- Número de ocasiones en que la máquina debe ser reparada.
- Si el beneficio neto es de 100 euros por cada día que la máquina está funcionando y una pérdida de 1500 euros por cada día que está en reparación ¿cuál es el beneficio esperado para el próximo año?
Obtenemos la simulación del sistema:
mu <- 1/60
lambda <- 1/4
simulacion <- TSIM_one_machine(mu, lambda, 365)
simulacion## # A tibble: 4 × 5
## tfun nfun trep nrep tsis
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 12.1 1 6.58 1 18.7
## 2 311. 2 3.41 2 333.
## 3 27.9 3 2.18 3 363.
## 4 1.42 4 2.28 4 370.Podemos ver que el número de ciclos en que la máquina ha entrado en funcionamiento es 4, mientras que el número de veces que ha necesitado reparación son 4.
Calculamos ahora los tiempos totales de funcionamiento y reparación:
## tfun trep
## 351.97978 14.44428Por tanto, la proporción de tiempo que la máquina está en funcionamiento es 0.96, y el beneficio estimado para el próximo año viene dado por:
beneficio <- 100 * tiempos["tfun"] - 1500 * tiempos["trep"]
beneficio## tfun
## 13531.564.3.2 Sistema del viajante
A continuación analizamos el sistema del viajante correspondiente al ejemplo 4.2. En primer lugar establecemos el algoritmo de simulación del sistema. Para facilitar todas las posibilidades del algoritmo asumimos que el vendedor comienza el recorrido en la ciudad en la que reside.
Algoritmo para el análisis del sistema del viajante:
- Fijar tasas de permanencia en cada ciudad \(\mu_A\), \(\mu_B\), y \(\mu_C\), así como las probabilidades de salto dadas en la matriz \(P\), y una variable que indica la ciudad en la que nos encontramos (\(ciudad\)).
- Fijar el tiempo de funcionamiento del sistema \(tsis = 0\), tiempo de permanencia en cada ciudad \(tiempo = 0\), y el tiempo de estudio \(tfin\).
- Generar \(tiempo \sim Exp(\mu_a)\) y actualizar \(tsis\), de forma que si \(tsis > tfin\) abandonamos el sistema.
- Generamos un salto de la ciudad \(A\) de acuerdo a las probabilidades de \(P\) correspondientes a la ciudad \(A\).
Repetir los pasos siguientes hasta que el tiempo en el sistema supere el tiempo fijado:
- Actualizamos \(ciudad\), generamos \(tiempo \sim Exp(\mu_{ciudad})\) y actualizamos \(tsis\), de forma que si \(tsis > tfin\) abandonamos el sistema.
- Generamos un salto de la ciudad del paso anterior de acuerdo a las probabilidades de \(P\) correspondientes a dicha ciudad.
Los valores \(tiempo\), y \(ciudad\) nos permiten describir el funcionamiento del sistema para un tiempo prefijado.
A continuación construimos la función para simular el sistema hasta cierto instante de tiempo.
TSIM_viajante <- function(tasaA, tasaB, tasaC, tfin)
{
# Parámetros de la función
# =========================
# tasaA: tasa de permanencia en A
# tasaB: tasa de permanencia en B
# tasaC: tasa de permanencia en C
# tfin: tiempo de funcionamiento del sistema
# inicialización de parámetros del sistema
tiempo = tsis = ciudad = vector()
# Probabilidades de salto. Fijamos la primera ya que la otra es complementaria
pA <- 0.5 # de A a B. De A a C es 1-pA
pB <- 0.75 # de B a A. De B a C es 1-pB
pC <- 0.75 # de C a A. De C a B es 1-pC
# estado inicial del sistema
i <- 1
ciudad[i] <- "A"
# Primer tiempo de estancia
tiempo[i] = rexp(1, tasaA)
tsis[i] <- tiempo[i]
# Saltamos de la ciudad A
uniforme <- runif(1)
ifelse(uniforme <= pA, ciudad[i+1] <- "B", ciudad[i+1] <- "C")
# Bucle de simulación
while(tsis[i] <= tfin)
{
i<- i + 1
uniforme <- runif(1)
if(ciudad[i] == "A")
{
# Calculamos tiempo de permanencia
tiempo[i] <- rexp(1, tasaA)
# Actualizamos y valoramos si hemos alcanzado el tiempo límite
tsis[i] = tsis[i-1] + tiempo[i]
if(tsis[i] > tfin){
tiempo[i] <- tfin - tsis[i-1]
tsis[i] = tsis[i-1] + tiempo[i]
break
}
# Si no hemos alcanzado el límite realizamos un nuevo salto
ifelse(uniforme <= pA, ciudad[i+1] <- "B", ciudad[i+1] <- "C")
}
if(ciudad[i] == "B")
{
# Calculamos tiempo de permanencia
tiempo[i] <- rexp(1, tasaB)
# Actualizamos y valoramos si hemos alcanzado el tiempo límite
tsis[i] = tsis[i-1] + tiempo[i]
if(tsis[i] > tfin){
tiempo[i] <- tfin - tsis[i-1]
tsis[i] = tsis[i-1] + tiempo[i]
break
}
# Si no hemos alcanzado el límite realizamos un nuevo salto
ifelse(uniforme <= pB, ciudad[i+1] <- "A", ciudad[i+1] <- "C")
}
if(ciudad[i] == "C")
{
# Calculamos tiempo de permanencia
tiempo[i] <- rexp(1, tasaC)
# Actualizamos y valoramos si hemos alcanzado el tiempo límite
tsis[i] = tsis[i-1] + tiempo[i]
if(tsis[i] > tfin){
tiempo[i] <- tfin - tsis[i-1]
tsis[i] = tsis[i-1] + tiempo[i]
break
}
# Si no hemos alcanzado el límite realizamos un nuevo salto
ifelse(uniforme <= pC, ciudad[i+1] <- "A", ciudad[i+1] <- "C")
}
}
# Devolvemos resultados del sistema
ciudad <- factor(ciudad)
res <- tibble(tiempo, ciudad, tsis)
return(res)
}Supongamos que estamos interesados en aproximar el comportamiento del vendedor durante el próximo año (52 semanas) para poder contestar a las preguntas siguientes:
- Proporción de tiempo que el vendedor pasa en cada ciudad.
- Número de ocasiones en que visita cada ciudad.
Simulamos pues el sistema y contestamos a las preguntas planteadas:
tasaA <- 1/2
tasaB <- 1/1
tasaC <- 2/3
tfin <- 52
simulacion <- TSIM_viajante(tasaA, tasaB, tasaC, tfin)
# Análisis del sistema
simulacion %>%
group_by(ciudad) %>%
summarise(visita = n(), estancia = sum(tiempo)) %>%
mutate(proporcion = estancia/52)## # A tibble: 3 × 4
## ciudad visita estancia proporcion
## <fct> <int> <dbl> <dbl>
## 1 A 16 32.1 0.617
## 2 B 7 6.27 0.121
## 3 C 10 13.6 0.2624.3.3 Análisis con simmer
Si bien dedicamos en este curso un capítulo entero para contar el funcionamiento de la librería simmer, puesto que estos ejemplos son relativamente sencillos, podemos introducir sin demasiada complicación el algoritmo de simulación con simmer.
La libreria simmer permite simular de sistemas tanto continuos como discretos bajos dos premisas fundamentales:
- Proceso de llegadas (“arrivals”) al sistema.
- Proceso de servicio (“server”): en el que a cada una de las llegadas se les asigna una serie de actividades a realizar (integradas en ‘trayectorias’) y unos recursos o servidores que resuelven con ellas las actividades.
Para el sistema descrito en ejemplo 4.5 el proceso de llegadas viene identificado por las averías que se producen en determinados instantes de tiempo. El proceso de servicio se corresponde con las reparaciones de las máquinas, a las que se dedica cierto tiempo. En este caso el recurso es el reparador encargado de resolver la avería y poner en marcha la máquina de nuevo.
El primer paso del algoritmo de simulación es cargar las librerías y definir la semilla de simulación:
library(tidyverse)
library(simmer)
library(simmer.plot)
library(simmer.bricks)
library(parallel)
set.seed(1234)Definimos ahora el entorno de simulación del sistema:
# Sistema
#################################################
sistema.1m <- function(t, lambda, mu)
{
# tarea dentro de sistema: reparación de las averías
reparar <- trajectory() %>%
# la máquina estropeada se asigna a un reparador
seize("reparador", amount = 1) %>%
# el tiempo de reparación es aleatorio
timeout(function() rexp(1, lambda)) %>%
# la máquina ya ha sido reparada
release("reparador", amount = 1)
# Configuración del sistema
#################################################
simmer() %>%
# Se definen los recursos: un único reparador y cola infinita
add_resource("reparador", capacity = 1) %>%
# Simulador de los tiempos entre averías, dirigidas a "reparar"
add_generator("averia", reparar, function() rexp(1, mu)) %>%
# Tiempo funcionamiento del sistema
run(until = t)
}
####################################
# Tasas de permanencia del sistema
######
lambda <- 1/4 # tasa reparación
mu <- 1/60 # tasa funcionamiento
### Simulación del sistema durante 365 días
operar <- sistema.1m(365, lambda,mu)Analizamos ahora los resultados que proporciona el sistema simulado. Podemos acceder a las información de dos formas diferentes mediante las funciones get_mon_arrivals() para describir las llegadas (averías) y get_mon_resources() para describir la ocupación de los servidores recursos (técnicos reparadores).
reparacion = get_mon_arrivals(operar)
reparacion## name start_time end_time activity_time finished replication
## 1 averia0 150.1055 150.1318 0.02632783 TRUE 1
## 2 averia1 164.9110 166.4598 1.54873033 TRUE 1
## 3 averia2 269.4758 272.7721 3.29632606 TRUE 1
## 4 averia3 274.8728 278.2250 3.35216128 TRUE 1
## 5 averia4 287.0299 294.5502 7.52030671 TRUE 1
## 6 averia5 332.6557 339.2903 6.63464954 TRUE 1El objeto resultante tiene las columnas siguientes:
-
name: nombre de las llegadas (averías), numeradas correlativamente -
star_time: instante en el que llega al sistema (se produce la avería) -
end_time: instante en el que sale del sistema (se ha reparado) -
activity_time: tiempo dedicado a la tarea (tiempo de reparación) -
finished: si la tarea ha finalizado dentro del periodo de tiempo de simulación establecido. -
replication: número de replicas del sistema (1 porque sólo hemos lanzado una cadena).
recursos = get_mon_resources(operar)
recursos## resource time server queue capacity queue_size system limit replication
## 1 reparador 150.1055 1 0 1 Inf 1 Inf 1
## 2 reparador 150.1318 0 0 1 Inf 0 Inf 1
## 3 reparador 164.9110 1 0 1 Inf 1 Inf 1
## 4 reparador 166.4598 0 0 1 Inf 0 Inf 1
## 5 reparador 269.4758 1 0 1 Inf 1 Inf 1
## 6 reparador 272.7721 0 0 1 Inf 0 Inf 1
## 7 reparador 274.8728 1 0 1 Inf 1 Inf 1
## 8 reparador 278.2250 0 0 1 Inf 0 Inf 1
## 9 reparador 287.0299 1 0 1 Inf 1 Inf 1
## 10 reparador 294.5502 0 0 1 Inf 0 Inf 1
## 11 reparador 332.6557 1 0 1 Inf 1 Inf 1
## 12 reparador 339.2903 0 0 1 Inf 0 Inf 1Con la función get_mon_resources() tenemos una descripción continua de los recursos del proceso con las columnas:
-
resource: recurso (numerado correlativamente si hubiera más de uno) -
time: instante de tiempo en que se ha registrado alguna actividad (avería, reparación, puesta en marcha) -
server: número de servidores (recursos) ocupados (como sólo hay un técnico, es igual a 1) -
queue: llegadas en la cola (averías que están esperando ser reparadas porque el técnico está ocupado) -
capacity: capacidad del sistema o número de reparadores en el sistema -
queue_size: tamaño de la cola de espera (averías en espera para ser reparadas) -
system: llegadas en el sistema (número de averías en ese instante, en reparación o en cola) -
limit: capacidad + tamaño de la cola -
replication: número de replica del sistema (1 porque sólo se ha lanzado una cadena).
A partir de los resultados podemos responder a las mismas preguntas que ya planteamos antes:
- Proporción del tiempo que la máquina está funcionando y en reparación.
- Número de ocasiones en que la máquina debe ser reparada.
- Si el beneficio neto es de 100 euros por cada día que la máquina está funcionando y una pérdida de 1500 euros por cada día que está en reparación ¿cuál es el beneficio esperado para el próximo año?
Para responder al primer pregunta basta con sumar los tiempos de actividad y calcular su proporción sobre los 365 días de simulación:
tiempo_reparacion <- sum(reparacion$activity_time)
propor <- round(100*(1-(tiempo_reparacion/365)), 2)
propor## [1] 93.87La proporción de tiempo en que la máquina está funcionando es del 93.87% y el tiempo que está en reparación es del 6.13%.
El número de ocasiones en que la máquina está en reparación corresponde al número de veces que accedemos a la tarea de reparación, que viene identificado por el número de averías, o lo que es equivalente, el número de veces que el reparador está ocupado (server=1), esto es,
sum(recursos$server==1)## [1] 6
nrow(reparacion)## [1] 6Para calcular el beneficio obtenido a lo largo del año utilizamos el tiempo de reparación obtenido:
(365-tiempo_reparacion)*100 - tiempo_reparacion*1500## [1] 694.3972Como se puede ver, los resultados no son muy similares a los obtenidos con el algoritmo que programamos nosotros. Para conseguir estimaciones eficientes deberíamos realizar diferentes replicaciones del sistema (lanzar varias cadenas) y promediar los beneficios obtenidos mediante un estimador Monte-Carlo. Podemos replicar fácilmente el sistema añadiendo dos líneas de código. Cada cadena replicada tendrá un distintivo diferente en el argumento ‘replicate’ cuando monitorizamos los resultados.
# lanzamos 'nreplicas' de la cadena, que se almacenan en una lista
nreplicas <- 500
envs <- mclapply(1:nreplicas, function(i){
sistema.1m(365, 1/4, 1/60) %>%
wrap()},mc.set.seed = FALSE)Ahora almacenamos todas las simulaciones a modo de matriz, en concreto ‘tibble,’ para poder realizar los cálculos oportunos agrupando por réplicas y con ellos poder calcular las estimaciones Monte-Carlo del tiempo total de reparación y del número de reparaciones.
# guardamos todas las llegadas en formato 'tibble'
simulaciones <- as_tibble(get_mon_arrivals(envs))
# agrupamos por 'replication' para calcular los descriptivos de interés en cada réplica
salida <- simulaciones %>%
group_by(replication) %>%
# Calculamos los descriptivos por cada réplica
summarise(nreparaciones = n(),
tiempoparada = sum(activity_time)) %>%
# Calculamos las estimaciones Monte-Carlo con los descriptivos de las réplicas
summarise(mmedia_nrepara = mean(nreparaciones),
min_nrepara = min(nreparaciones),
max_nrepara = max(nreparaciones),
media_taveria = mean(tiempoparada),
q25_taveria = quantile(tiempoparada, 0.25),
q50_taveria = quantile(tiempoparada, 0.50),
q75_taveria = quantile(tiempoparada, 0.75),
sd_taveria = sd(tiempoparada)
)
salida## # A tibble: 1 × 8
## mmedia_nrepara min_nrepara max_nrepara media_taveria q25_taveria q50_taveria q75_taveria
## <dbl> <int> <int> <dbl> <dbl> <dbl> <dbl>
## 1 5.96 1 14 23.6 12.9 21.3 32.1
## # … with 1 more variable: sd_taveria <dbl>En ‘mmedia_nrepara’ tenemos la estimación del número de reparaciones en un año, en ‘min_nrepara’ y ‘max_nrepara’ el mínimo y el máximo respectivamente; en ‘media_taveria’ tenemos una estimación del tiempo medio acumulado en reparaciones en un año, con sus cuartiles (q25, q50 y q75) y desviación típica (sd).
Así podemos calcular los beneficios esperados en función del número de días que la máquina funciona y los que está estropeada:
# número de días en funcionamiento vs número de días en reparación
(365-salida$media_taveria)*100 - salida$media_taveria*1500## [1] -1221.145Podemos considerar también otros dos escenarios posibles: uno pesimista, con un mayor tiempo acumulado de reparación (cuantil 75), y uno optimisma, con un menor tiempo (con el cuantil 25), y calcular con ellos los beneficios:
(365-salida$q75_taveria)*100 - salida$q75_taveria*1500## 75%
## -14854.3
(365-salida$q25_taveria)*100 - salida$q25_taveria*1500## 25%
## 15835.39¿Qué conclusiones podemos extraer de este análisis?
Para finalizar este apartado presentamos un nuevo ejemplo donde el espacio de estados está compuesto por una pareja de valores y no por un único valor como en los ejemplos que hemos presentado hasta ahora.
4.3.4 Mantenimiento de aronaves
Una empresa de mantenimiento de aeronaves está interesada en el proceso de avería-reparación de cierto tipo de aviones. El tipo de avión de interés es un avión comercial a reacción con cuatro motores, dos en cada ala. Cuando un motor se enciende, el tiempo que se puede mantener en funcionamiento hasta que falla es una variable aleatoria exponencial con parámetro \(\lambda\). Si el fallo se produce en vuelo, no puede haber reparación, pero el avión necesita al menos un motor en cada ala para funcionar correctamente y poder volar con seguridad. En concreto, la empresa está interesada en poder predecir la probabilidad de un vuelo sin problemas.
Si denotamos por \(X_L(t)\) y \(X_R(t)\) el número de motores funcionando en el instante \(t\) en el ala izquierda y el ala derecha respectivamente, podemos considerar el estado del sistema en el instante \(t\) como \(X_t = (X_L(t), X_R(t))\). Si asumimos que los fallos en los motores son independientes entre sí, podemos ver que el proceso \(\{X_t, t \geq 0\}\) es una CMTC con espacio de estados:
\[S = \{ (0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2,2) \}\]
En esta situación, el avión sigue funcionando en el subconjunto de estados \(S = \{ (1, 1), (1, 2), (2, 1), (2,2) \}\).
Vamos a asumir (aunque no es real) que el sistema sigue funcionando, incluso cuando hay posibilidad de un accidente, hasta que llegamos al estado \((0, 0)\). Dado que no hay reparación posible, la matriz de tasas entre estados del sistema viene dada por
\[R = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \lambda & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2\lambda & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \lambda & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \lambda & 0 & \lambda & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \lambda & 0 & 2\lambda & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2\lambda & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2\lambda & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2\lambda & 0 & 2\lambda & 0 \end{pmatrix} \]
y el diagrama que representa el sistema resulta:
Figura 4.4: Diagrama de tasas para el sistema motores de aviones
Para facilitar el algoritmo de simulación en esta situación, vamos a asignar un código a cada uno de los posibles estados del sistema:
\[S = \{ 1 = (0, 0), 2 = (0, 1), 3 = (0, 2), 4 = (1, 0), 5 = (1, 1), 6 = (1, 2), 7 = (2, 0), 8 = (2, 1), 9 = (2,2) \}\]
y asumimos que la media del tiempo hasta que un motor falla cuando está encendido es de 20 horas, es decir, \(\lambda = 1/20\). A continuación hemos construido una función para simular el sistema descrito:
TSIM_aviones <- function(tasa)
{
# Parámetros de la función
# =========================
# tasa: tasa de fallo de un motor
# Valores fijos del sistema
# codigos de motores funcionando obviando el estado inicial
codigo <- 1:8
# motores con fallo de acuerdo al código
motoresOFF <- c(4, 3, 2, 3, 2, 1, 2, 1)
# inicialización de parámetros del sistema
tiempo = estado = fallos = vector()
i<-1
# Primer fallo
# Posibles estados de salto
saltos = c(codigo[6], codigo[8])
# tiempos asociados a cada fallo
simula = rexp(2, 2*tasa)
# Seleccionamos el salto
posicion = which.min(simula)
if(posicion == 1)
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# nuevo salto
i <- i + 1
saltos = c(codigo[3], codigo[5])
simula = c(rexp(1, tasa), rexp(1, 2*tasa))
posicion = which.min(simula)
if(posicion == 1)
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# dos últimos saltos
estado[i+1] <- 2; estado[i+2] <- 1
tiempo[i+1] <- rexp(1, 2*tasa); tiempo[i+2] <- rexp(1, tasa)
fallos[i+1] <- motoresOFF[estado[i+1]]; fallos[i+2] <- motoresOFF[estado[i+2]]
}
else
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# dos últimos saltos
estado[i+1] <- 2; estado[i+2] <- 1
tiempo[i+1] <- rexp(1, tasa); tiempo[i+2] <- rexp(1, tasa)
fallos[i+1] <- motoresOFF[estado[i+1]]; fallos[i+2] <- motoresOFF[estado[i+2]]
}
}
else
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# nuevo salto
i <- i + 1
saltos = c(codigo[7], codigo[5])
simula = c(rexp(1, tasa), rexp(1, 2*tasa))
posicion = which.min(simula)
if(posicion == 1)
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# dos últimos saltos
estado[i+1] <- 2; estado[i+2] <- 1
tiempo[i+1] <- rexp(1, 2*tasa); tiempo[i+2] <- rexp(1, tasa)
fallos[i+1] <- motoresOFF[estado[i+1]]; fallos[i+2] <- motoresOFF[estado[i+2]]
}
else
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# dos últimos saltos
estado[i+1] <- 2; estado[i+2] <- 1
tiempo[i+1] <- rexp(1, tasa); tiempo[i+2] <- rexp(1, tasa)
fallos[i+1] <- motoresOFF[estado[i+1]]; fallos[i+2] <- motoresOFF[estado[i+2]]
}
}
# Devolvemos resultados del sistema
res <- tibble(estado, tiempo, fallos)
return(res)
}Veamos una simulación del sistema:
set.seed(12)
tasa <- 1/20
sistema <- TSIM_aviones(tasa)
sistema## # A tibble: 4 × 3
## estado tiempo fallos
## <dbl> <dbl> <dbl>
## 1 8 6.36 1
## 2 7 2.35 2
## 3 2 18.2 3
## 4 1 5.67 4El resultado obtenido es el estado en cada paso del algoritmo hasta llegar a la parada total, los tiempos para alcanzar cada estado, y el número de motores con fallo.
Podemos operar los tiempos para saber cuándo tendremos más de dos motores con fallo (últimas dos filas de la simulación).
Si el vuelo que acabamos de empezar es de \(x\) horas ¿cómo podemos estimar la probabilidad de no poder terminar el vuelo de forma segura? Para responder esta pregunta podremos calcular la proporción de tiempo que corresponde con un fallo leve (1 o 2 motores con fallo) con respecto a las \(x\) horas de duración del vuelo.
Calculamos a continuación el tiempo de fallo del sistema y evaluamos la probabilidad para diferentes tiempos de duración de vuelo.
# Tiempo de fallo
Tfallo <- round(sum(sistema$tiempo[sistema$fallos <= 2]), 2)
# Duración del vuelo
td <- seq(0.1, 12, by = 0.1)
prob <- vector()
# Probabilidad viaje seguro
for(i in 1:length(td))
{
prob[i] <- ifelse(Tfallo >= td[i], 1, round(Tfallo/td[i], 3))
}
# Obtenemos el valor mínimo de tiempo para asegurar un viaje seguro
limite <- min(td[which(prob != 1)])
limite## [1] 8.8Cualquier viaje inferior a 8.8 horas será un viaje seguro, mientras que si el tiempo es superior, la probabilidad de no tener un viaje seguro aumenta.
Para estudiar la estabilidad de dichas probabilidades realizamos 1000 simulaciones del sistema y estimamos las probabilidades mediante estimadores Monte-Carlo de los tiempos de fallo.
nsim <- 1000
Tfallo <- vector()
# Repetición del sistema y calculo de tiempo
for(i in 1:nsim)
{
sistema <- TSIM_aviones(tasa)
Tfallo[i] <- round(sum(sistema$tiempo[sistema$fallos <= 2]), 2)
}
# Estimador Monte-Carlo
estimMC<- mean(Tfallo)
# Duración del vuelo
td <- seq(0.1, 20, by = 0.1)
prob <- vector()
# Probabilidad viaje seguro
for(i in 1:length(td))
{
prob[i] <- ifelse(estimMC >= td[i], 1, round(estimMC/td[i], 3))
}
# Obtenemos el valor mínimo de tiempo para asegurar un viaje seguro
limite <- min(td[which(prob != 1)])
limite## [1] 11.9Cualquier viaje inferior a 11.9 horas será un viaje seguro, mientras que si el tiempo es superior, la probabilidad de no tener un viaje seguro aumenta. Podemos representar el gráfico de probabilidad de un viaje seguro:
Figura 4.5: Probabilidad de un viaje seguro
4.4 Procesos de nacimiento y muerte
Los procesos de nacimiento y muerte que estudiamos en este apartado juegan un papel muy importante dentro de las CMTC, ya que son de uso habitual en muchas aplicaciones prácticas que veremos de ahora en adelante.
Veamos cierta propiedad que nos va a resultar de interés.
Supongamos que en un instante \(t\), el sistema está en estado \(i\), esto es, \(X_t=i\), y qe es posible transitar al estado \(j\) a través de la ocurrencia de \(m\) eventos independientes, cada uno de los cuales se produce con tiempos independientes \(T_i \sim Exp(\lambda_i)\).
Es el caso de que haya 5 máquinas funcionando en un sistema y cualquiera de las 5 puede fallar, de manera que un fallo en cualquiera de ellas produciría una transición al estado 4 (4 máquinas funcionando).
Entonces el sistema permanecerá en el estado \(i\) hasta que se produzca el primer evento de los \(m\) posibles, esto es, el tiempo de permanencia en el estado \(i\), \(TP_i\), será el mínimo de los tiempos de ocurrencia de los \(m\) eventos, y su distribución será exponencial de tasa la suma de las tasas de ocurrencia de los \(m\) eventos, esto es:
\[TP_i=min\{T_1,\ldots,T_m\} \sim Exp(\lambda), \qquad \text{con } \lambda=\sum_{i=1}^m \lambda_i.\]
En este caso, la tasa de permanencia es \(r_i=\lambda\), la probabilidad de salto al estado \(j\), \(p_{ij}=1\) y la tasa de transición al estado \(j\) es \(r_{ij}=\lambda\).
Definición 4.2 Una CMTC \(\{X_t; t \geq 0\}\) con espacio de estados \(S = \{0, 1, 2,...,N\}\) y matriz de tasas dada por:
\[R = \begin{pmatrix} 0 & \lambda_0 & 0 & 0 & \ldots & 0 & 0 \\ \mu_1 & 0 & \lambda_1 & 0 & \ldots & 0 & 0 \\ 0 & \mu_2 & 0 & \lambda_2 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ldots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & 0 & \lambda_{N-1} \\ 0 & 0 & 0 & 0 & \ldots &\mu_N & 0 \end{pmatrix} \]
se denomina proceso finito de nacimiento y muerte donde los \(\lambda_i\) se denominan parámetros de nacimiento (transición del estado \(i\) al \(i+1\)) y los \(\mu_i\) se denominan parámetros de muerte (transición del estado \(i\) al \(i-1)\), donde por conveniencia se asume que \(\lambda_N = 0\) y \(\mu_0 = 0\) indicando que no hay nacimientos en el estado \(N\) y que no hay muertes en el estado \(0\).
En esta situación el proceso permanece en el estado \(i\) un tiempo \(Exp(\lambda_i + \mu_i)\), de modo que la tasa media de permanencia en el estado \(i\) es \(r_i=\lambda_i+\mu_i\). Después salta al estado \(i+1\) con probabilidad \(p_{i,i+1}=\lambda_i/(\lambda_i + \mu_i)\), o al estado \(i-1\) con probabilidad \(p_{i,i-1}=\mu_i/(\lambda_i + \mu_i)\). Además, la matriz generadora del proceso viene dada por:
\[Q = \begin{pmatrix} - \lambda_0& \lambda_0 & 0 & 0 & \ldots & 0 & 0 \\ \mu_1 & -(\mu_1 + \lambda_1) & \lambda_1 & 0 & \ldots & 0 & 0 \\ 0 & \mu_2 & -(\mu_2 + \lambda_2) & \lambda_2 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ldots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & -(\mu_{N-1} + \lambda_{N-1}) & \lambda_{N-1} \\ 0 & 0 & 0 & 0 & \ldots & \mu_N & -\mu_N \end{pmatrix} \]
A continuación presentamos diferentes ejemplos de aplicación de los procesos de nacimiento y muerte.
4.4.1 Cajero Bancario
Aunque en la unidad siguiente estudiaremos con mucho más detalle los diferentes sistemas de colas de espera, vamos a presentar aquí el modelo más sencillo de colas, para comprobar que se puede modelar como un proceso de nacimiento y muerte.
Imaginemos que tenemos un cajero bancario al que los clientes acuden de acuerdo a un Proceso de Poisson de parámetro \(\lambda\), es decir que las llegadas son aleatorias y se distribuyen según una distribución \(Exp(\lambda)\). El sistema tiene capacidad \(K\): 1 cliente atendido y \(K-1\) en la cola de espera. Además, el tiempo de servicio del cajero tiene una distribución \(Exp(\mu)\).
En esta situación la variable \(X_t\) que indica el número de sujetos en el sistema en el instante \(t\) es una CMTC denominada cola \(M/M/1/K\), donde \(M\) hace referencia a los tiempos de llegada y servicio exponenciales, el \(1\) hace referencia a la capacidad del servicio (sólo hay un cajero, luego sólo un cliente puede ser atendido en un instante dado), \(K\) es la capacidad del sistema (o aforo total), y \(S = \{0, 1, 2,...K \}\) el espacio de estados. Este tipo de sistemas son procesos de nacimiento y muerte con:
\[\begin{eqnarray*} \lambda_i &=& \lambda, \quad 0 \leq i \leq K-1, \\ \mu_i &=& \mu, \quad 1 \leq i \leq K, \end{eqnarray*}\]donde el “nacimiento” y la “muerte” hacen referencia a la llegada y la salida del cajero respectivamente.
Veamos la descripción del sistema:
En el estado \(X_t=0\) el sistema está vacío y el único evento que puede ocurrir es una llegada, que se produce después de un tiempo \(h \sim Exp(\lambda)\), provocando una transición al estado \(X_{t+h}=1\). En este caso \(r_{01} = \lambda\).
En el estado \(i\) (\(1 \leq i \leq K-1\)), tenemos dos posibilidades en el sistema: una llegada o una salida. En el primer caso tenemos \(r_{i, i+1} = \lambda\), mientras que en el segundo tenemos \(r_{i, i-1} = \mu\).
En el estado \(X_t=K\) sólo se puede producir una salida de forma que \(r_{K, K-1} = \mu\).
Por tanto, la matriz de tasas correspondiente a este proceso viene dada por:
\[R = \begin{pmatrix} 0 & \lambda & 0 & 0 & \ldots & 0 & 0 \\ \mu & 0 & \lambda & 0 & \ldots & 0 & 0 \\ 0 & \mu & 0 & \lambda & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ldots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & 0 & \lambda \\ 0 & 0 & 0 & 0 & \ldots &\mu & 0 \end{pmatrix} \]
El diagrama de tasas para una cola \(M/M/1/4\), es decir con una capacidad de 4 usuarios en el sistema (1 atendido y tres en espera) es:
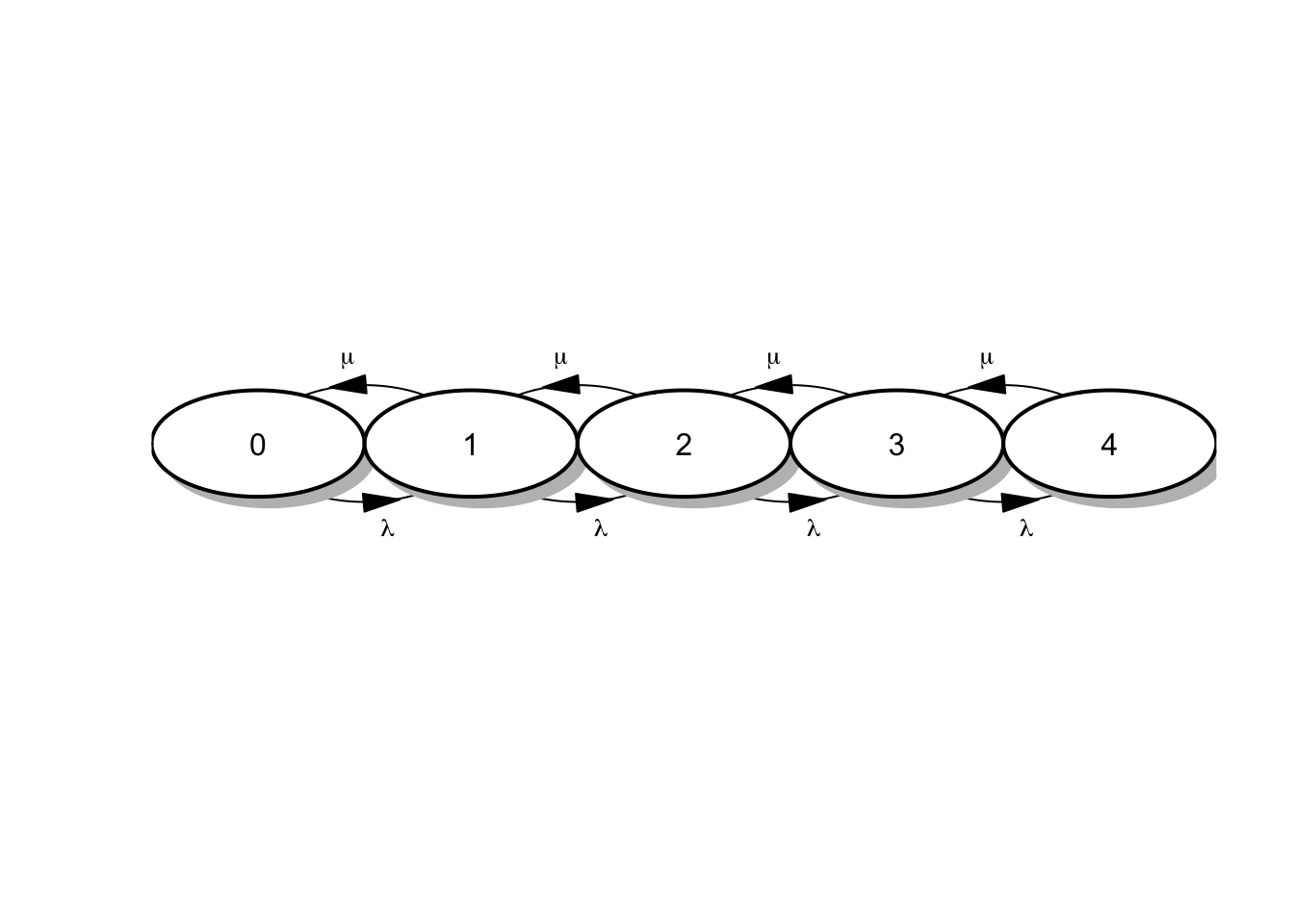
Figura 4.6: Diagrama de tasas para cola M/M/1/4.
Este sistema puede implementarse fácilmente en simmer si entendemos como recursos (resource) el cajero, con un tiempo de servicio dado por \(Exp(\mu)\) y como fuentes (generator) la llegada de clientes al cajero, con tiempos entre llegadas \(Exp(\lambda)\). Escribimos el algoritmo de forma general para cualquier valor de \(K\).
# Sistema
#################################################
cola.MM1K <- function(t, lambda, mu, servidores, usuarios)
{
# lambda: tasa de llegadas
# mu: tasa de servicio
# servidores: número de servidores
# usuarios: capacidad total del sistema
cola <- usuarios - servidores
servicio <- trajectory() %>%
# empieza a ser atendido
seize("atendiendo", amount = 1) %>%
# durante un tiempo exp(mu)
timeout(function() rexp(1, mu)) %>%
# termina el servicio de atención
release("atendiendo", amount = 1)
# Configuración del sistema
#################################################
simmer() %>%
# se crean los recursos (servidores) y se dimensiona la cola
add_resource("atendiendo", capacity = servidores, queue_size = cola) %>%
# se generan las llegadas de clientes según Exp(lambda)
add_generator("llegada", servicio, function() rexp(1, lambda)) %>%
run(until = t)
}Ejemplo 4.6 Imaginemos que por la mañanas (de 8 a 15) las llegadas de clientes se producen con una tasa de 15 clientes/hora, mientras que el tiempo medio que el cliente permanece en el cajero es de 6 minutos. Expresada en minutos tendríamos una tasa de llegadas \(\lambda = 15/60\), y una tasa de servicio \(\mu = 1/6\). Se ha observado además que cuando la cola de espera es de tres clientes nadie más espera para hacer cola (\(K = 4\)). Analizamos el sistema de forma básica para una mañana cualquiera, es decir para un periodo de 7 horas (420 minutos).
set.seed(12)
### Simulación del sistema
t=420;
lambda=15/60; mu=1/6
servidores=1; usuarios=4
cajero <- cola.MM1K(t, lambda, mu, servidores, usuarios)
### Salidas del sistema
cajero.df.res <- get_mon_resources(cajero) # recursos (servidores)
cajero.df.arr <- get_mon_arrivals(cajero) # llegadas (clientes)Veamos con un poco de detalle las salidas que proporciona el sistema. Comenzamos con el proceso de llegadas al sistema viendo las primeras 10 llegadas al sistema:
# llegadas
head(cajero.df.arr, n = 10)## name start_time end_time activity_time finished replication
## 1 llegada0 8.756865 9.461164 0.704299 TRUE 1
## 2 llegada1 11.299066 22.198513 10.899446 TRUE 1
## 3 llegada2 22.728061 46.307530 23.579469 TRUE 1
## 4 llegada7 53.191599 53.191599 0.000000 FALSE 1
## 5 llegada3 23.861384 53.496376 7.188846 TRUE 1
## 6 llegada9 57.528321 57.528321 0.000000 FALSE 1
## 7 llegada4 40.759227 59.558394 6.062018 TRUE 1
## 8 llegada11 68.130173 68.130173 0.000000 FALSE 1
## 9 llegada12 74.418248 74.418248 0.000000 FALSE 1
## 10 llegada5 45.814971 75.428935 15.870541 TRUE 1En la columna name tenemos el identificador de la llegada al sistema (cajero), en las columnas start_time y end_time tenemos el instante de tiempo en el que llega y sale del cajero. La columna activity_time muestra el tiempo de servicio en el cajero (durante el que es atendido el cliente); un valor 0 identifica a un cliente que no ha sido atendido porque sobrepasó la capacidad del sistema (no esperó al ver la cola y se marchó). Estos coinciden con los valores FALSE de la columna finished, que identifica a los clientes que no han podido ser atendidos. Con estas salidas resulta muy fácil calcular el tiempo de servicio del sistema así como el porcentaje de clientes rechazados, y el tiempo esperando en la cola.
# llegadas al sistema: número de clientes que han pasado por el cajero
nsis <- nrow(cajero.df.arr);nsis## [1] 108
# tiempo total de servicio
tserver <- sum(cajero.df.arr$activity_time);tserver## [1] 407.9837
# proporción de tiempo que el sistema está ocupado (atendiendo o en espera)
round(100*tserver/t,2)## [1] 97.14
# porcentaje de clientes que se marcharon sin ser atendidos
rechazados <- sum(cajero.df.arr$finished == FALSE)
round(100*rechazados/nsis,2)## [1] 48.15
# Tiempos de espera en cola para ser atendido
tespera <- cajero.df.arr$end_time - cajero.df.arr$start_time - cajero.df.arr$activity_time
# tiempo medio de espera en cola y desv.típica
mean(tespera);sd(tespera)## [1] 8.280251## [1] 10.53434Podemos estudiar el comportamiento del sistema, y en particular de la cola, también en términos de los servidores.
head(cajero.df.res, n = 10)## resource time server queue capacity queue_size system limit replication
## 1 atendiendo 8.756865 1 0 1 3 1 4 1
## 2 atendiendo 9.461164 0 0 1 3 0 4 1
## 3 atendiendo 11.299066 1 0 1 3 1 4 1
## 4 atendiendo 22.198513 0 0 1 3 0 4 1
## 5 atendiendo 22.728061 1 0 1 3 1 4 1
## 6 atendiendo 23.861384 1 1 1 3 2 4 1
## 7 atendiendo 40.759227 1 2 1 3 3 4 1
## 8 atendiendo 45.814971 1 3 1 3 4 4 1
## 9 atendiendo 46.307530 1 2 1 3 3 4 1
## 10 atendiendo 48.326016 1 3 1 3 4 4 1En este caso las columnas nos informan sobre el instante de tiempo (time) en el que se produce alguna actividad en el sistema, la columna server indica el número de servidores ocupados atendiendo a algún cliente, queue el número de clientes en la cola de espera, capacity la capacidad de servicio del sistema, queue_size el tamaño máximo de la cola, system el número de clientes en el sistema, limit la capacidad total de sistema, y finalmente replication da un indicador de la replicación de las simulaciones.
Con estas salidas podemos describir fácilmente el comportamiento de la cola del sistema ya que podemos estudiar el número de clientes en cola a lo largo del tiempo.
# Evolución del tamaño de la cola
ggplot(cajero.df.res, aes(time, queue)) +
geom_step() +
scale_x_continuous(breaks = seq(0, 420, 60)) +
labs(x = "Tiempo (en minutos)", y = "Tamaño de la cola")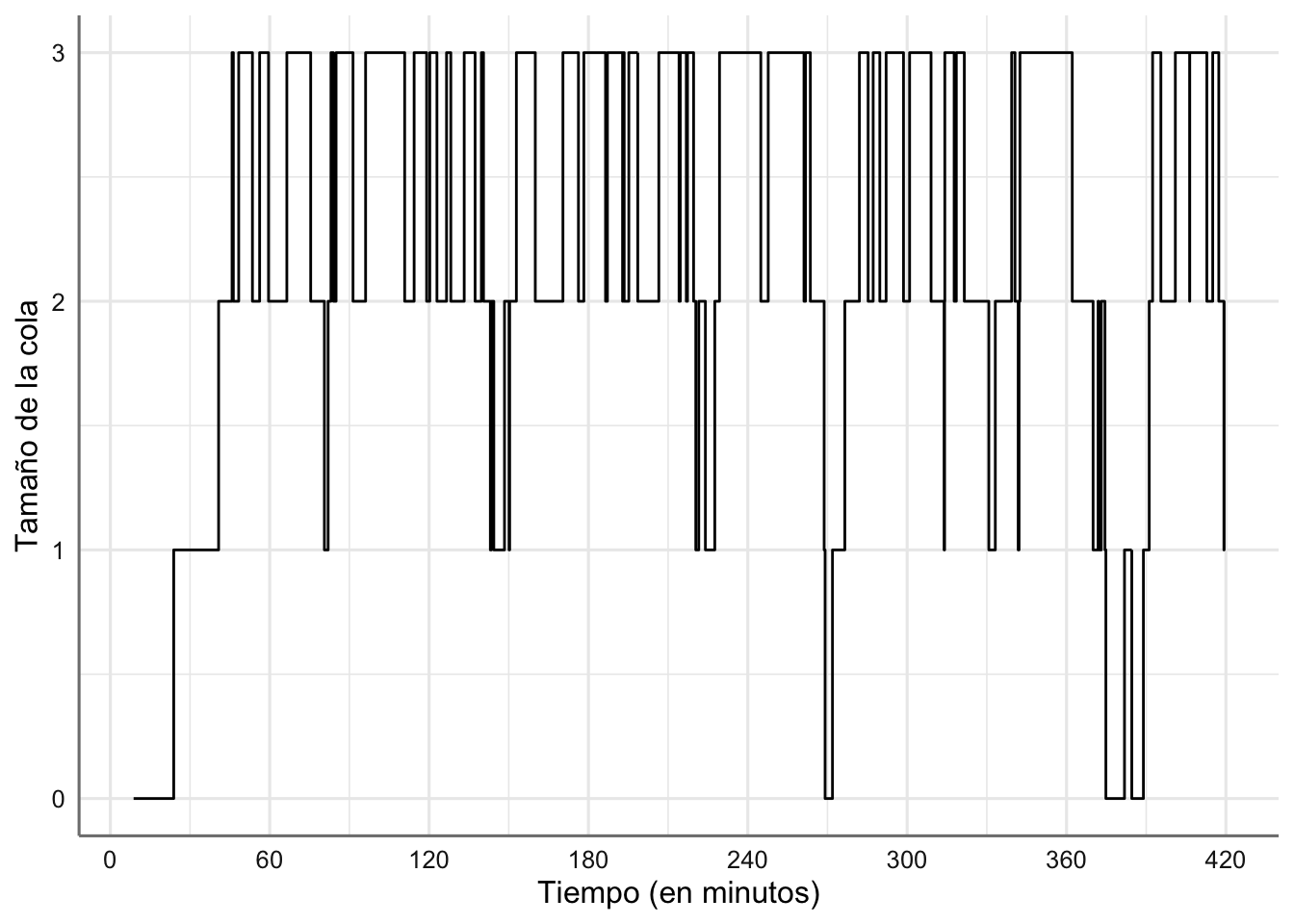
# Porcentaje de clientes en cola
ggplot(cajero.df.res, aes(x = queue)) +
geom_bar(aes(y = ..prop.. , group = 1)) +
scale_y_continuous(labels = scales::percent) +
labs(x = "Clientes en la cola", y = "Porcentaje")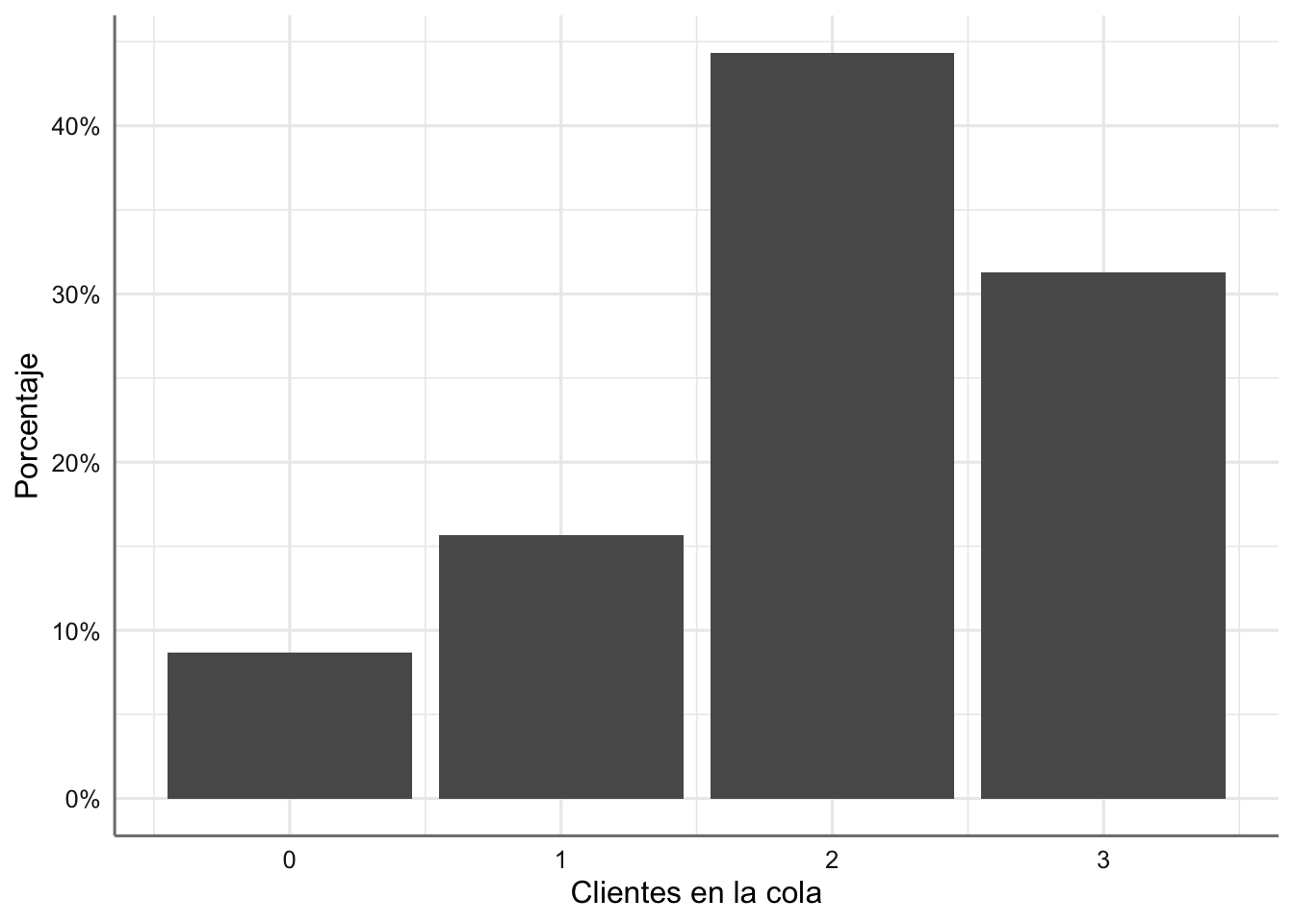
Simulamos ahora el sistema para 500 jornadas con las que inferir sobre el comportamiento medio del sistema.
# Réplicas del sistema
nreplicas=500
t=420;
lambda=15/60; mu=1/6
servidores=1; usuarios=4
envs <- replicate(nreplicas,cola.MM1K(t, lambda, mu, servidores, usuarios))
# almacenamos análisis de llegadas del sistema
simarrivals<-as_tibble(get_mon_arrivals(envs))
salida<-simarrivals %>%
group_by(replication) %>%
# Resumen de las simualciones
summarise(clientes = n(),
tiemposervicio = sum(activity_time),
proptiemposervicio = round(tiemposervicio/420, 2),
rechazados = clientes - sum(finished),
proprechazados = round(rechazados/clientes,2)) %>%
summarise(media_clientes = mean(clientes),
media_tserver = mean(tiemposervicio),
media_ptserver = 100*mean(proptiemposervicio),
media_rechazados = mean(rechazados),
media_prechazados = 100*mean(proprechazados)
)
salida## # A tibble: 1 × 5
## media_clientes media_tserver media_ptserver media_rechazados media_prechazados
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 102. 377. 89.8 37.9 36.7Para comentar: ¿Qué conclusiones extraemos del análisis realizado? ¿Cómo valorarías la ocupación del sistema? ¿Qué ocurriría si añadimos un nuevo cajero y ampliamos la capacidad del sistema a 8 clientes?
4.4.2 Mantenimiento de máquinas
El problema del mantenimiento de máquinas es muy habitual dentro de las CMTC. Supongamos que disponemos de \(N\) máquinas que funcionan durante 24 horas seguidas y \(M\) personas que pueden repararlas (\(M \leq N\)). Las máquinas son idénticas, y los tiempos de vida de las máquinas (tiempo hasta fallo o mantenimiento) son variables aleatorias independientes \(Exp(\lambda)\). Cuando las máquinas fallan, son reparadas por orden de fallo (la primera que falla es la primera en ser reparada) por los \(M\) reparadores. Cada máquina averiada necesita una y sólo una persona para repararla, y los tiempos de reparación se distribuyen como una \(Exp(\mu)\); una vez reparada, la máquina continúa comportándose como una máquina nueva. Si \(X_t\) es el número de máquinas estropeadas en el momento \(t\), el proceso \(\{X_t, t \geq 0\}\) es un proceso de nacimiento (avería) y muerte (reparación) con parámetros:
\[\begin{eqnarray*} \lambda_i &=& \lambda \cdot (N-i), \quad 0 \leq i < N\\ \mu_i &=& \mu \cdot min(i,M), \quad 0 < i \leq N \\ \end{eqnarray*}\]Ejemplo 4.7 Supongamos el problema de mantenimiento de máquinas en el que tenemos 4 máquinas y 2 reparadores. El espacio de estados (número de máquinas estropeadas) viene dado por \(S = \{0, 1, 2, 3, 4\}\).
La empresa está interesada en saber:
- ¿Cuántas máquinas estarán en funcionamiento después de una semana?
- ¿Cuánto tiempo están funcionando a la vez las cuatro máquinas (en términos porcentuales)?
- ¿Cuánto tiempo de funcionamiento se pierde por averías?
Comprobemos que podemos modelizar el sistema como un proceso de nacimiento-muerte.
Descripción del sistema:
En el estado \(X_t=0\), ninguna máquina está estropeada. Cuando ocurra una avería en un instante \(Exp(\lambda)\), tendremos 1 máquina estropeada, y la tasa de nacimientos (averías) cuando hay 0 averías es igual a la tasa de averías multiplicada por el número de máquinas que pueden estropearse, esto es, \(r_{01}=\lambda_0=4\lambda\).
En el estado \(X_t=1\) sólo una máquina está estropeada, de modo que entra en reparación. Las otras tres están en funcionamiento, de modo que la tasa de transición al estado 2, esto es, que una máquina más se estropee, será de \(r_{12}=\lambda_1=3\lambda\). Por otro lado, la tasa de reparación será \(r_{10}=\mu_1=\mu\).
En el estado \(X_t=2\), con razonamientos similares, tendremos que \(r_{23} = \lambda_2 = 2\lambda\) y \(r_{21} = \mu_2 = 2\mu\).
Para el resto de estados tendremos que \(r_{34} = \lambda_3 = \lambda\), \(r_{32} = mu_3 = 3\mu\), y \(r_{43} = \mu_4 = 4\mu\).
En esta situación el diagrama del proceso viene dado por:
estados <- c(0, 1, 2, 3, 4)
nestados <- length(estados)
M <- matrix(nrow = nestados, ncol = nestados, data = 0)
R <- as.data.frame(M)
R[[1,2]] <- "4*lambda"
R[[2,1]] <- "mu"
R[[2,3]] <- "3*lambda"
R[[3,2]] <- "2*mu"
R[[3,4]] <- "2*lambda"
R[[4,3]] <- "2*mu"
R[[4,5]] <- "lambda"
R[[5,4]] <- "2*mu"
# library(diagram)
pp <- plotmat(t(R), pos = 5, curve = 0.5, name = estados,
lwd = 1, box.lwd = 2, cex.txt = 0.8,
box.type = "circle", box.prop = 0.5, arr.type = "triangle",
arr.pos = 0.55, self.cex = 0.6,
shadow.size = 0.01, prefix = "", endhead = FALSE, main = "")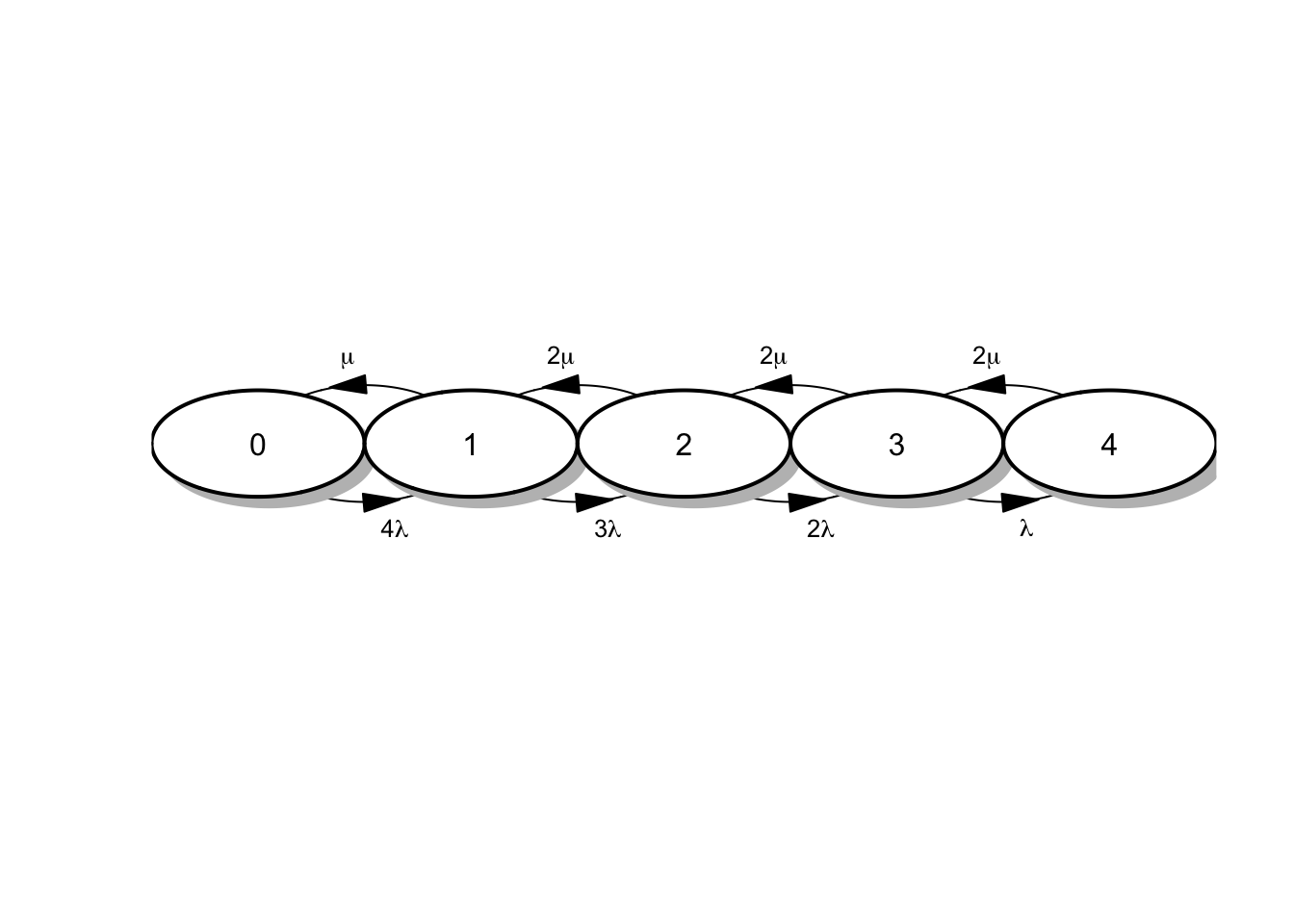
Figura 4.7: Diagrama de tasas para el mantenimiento de máquinas
Este sistema se puede modelizar fácilmente en simmer sin más que fijar las tasas correspondientes, el número de máquinas disponibles, y el número de operarios. Supongamos que los tiempos de vida de las máquinas son variables aleatorias exponenciales con media de 3 días, mientras que los tiempos de reparación son variables exponenciales con media de 2 horas. Expresando todo en horas, tendríamos una tasa de reparación de \(\mu = 1/2\), y una tasa de llegadas (averías) \(\lambda = 1/72\).
De nuevo planteamos una función que nos permita cambiar fácilmente los parámetros del sistema si fuera necesario. Para simular el sistema hemos de considerar que tenemos 4 máquinas idénticas que cuando se averían han de ser reparadas hasta volver a estar operativas y, en consecuencia, poder volver a estropearse. Es preciso pues, diferenciar las 4 máquinas y utilizar activadores y desactivadores que avisen al sistema de simulación de qué máquina está estropeada y cuál operativa y puede volver a averiarse.
# Sistema
#################################################
mantenimiento <- function(t, lambda, mu, capacidad,K)
{
env=simmer()
# lambda: tasa de averías
# mu: tasa de reparación
# capacidad: reparadores
# K: máquinas
reparacion <- function(i){
trajectory() %>%
# mientras reparo la máquina no se puede producir otro fallo
deactivate(paste0("maq",i,"_"))%>%
seize("mecanico",1) %>%
# tiempos de reparación
timeout(function() rexp(1,mu)) %>%
activate(paste0("maq",i,"_")) %>%
release("mecanico")}
# simulación de averías para K máquinas
for(i in 1:K) env %>%
add_generator(paste0("maq",i,"_"),reparacion(i),function() rexp(1,lambda))
env %>%
add_resource("mecanico", capacity = capacidad)%>%
run(until = t)
}Simulamos el sistema y analizamos la salida.
t=24*7 # tiempo de simulación (en horas)
lambda=1/72; mu=1/2
capacidad=2 # nº reparadores
K=4 # nº máquinas
### Simulación del sistema
sim <- mantenimiento(t, lambda,mu, capacidad,K)
### Salidas del sistema
sim.arr <- get_mon_arrivals(sim)
sim.res <- get_mon_resources(sim)
head(sim.arr, 10)## name start_time end_time activity_time finished replication
## 1 maq1_0 39.64840 40.91384 1.2654324 TRUE 1
## 2 maq2_0 63.84362 65.62617 1.7825544 TRUE 1
## 3 maq1_1 88.73081 92.10658 3.3757723 TRUE 1
## 4 maq4_0 96.17729 96.27956 0.1022763 TRUE 1
## 5 maq1_2 107.52619 108.46549 0.9393034 TRUE 1
## 6 maq3_0 109.80081 113.18065 3.3798393 TRUE 1
## 7 maq1_3 145.04424 146.34587 1.3016268 TRUE 1
## 8 maq1_4 148.19267 153.96245 5.7697764 TRUE 1
## 9 maq2_1 153.04616 156.24107 3.1949067 TRUE 1
## 10 maq2_2 158.09906 161.24654 3.1474876 TRUE 1
head(sim.res, 10)## resource time server queue capacity queue_size system limit replication
## 1 mecanico 39.64840 1 0 2 Inf 1 Inf 1
## 2 mecanico 40.91384 0 0 2 Inf 0 Inf 1
## 3 mecanico 63.84362 1 0 2 Inf 1 Inf 1
## 4 mecanico 65.62617 0 0 2 Inf 0 Inf 1
## 5 mecanico 88.73081 1 0 2 Inf 1 Inf 1
## 6 mecanico 92.10658 0 0 2 Inf 0 Inf 1
## 7 mecanico 96.17729 1 0 2 Inf 1 Inf 1
## 8 mecanico 96.27956 0 0 2 Inf 0 Inf 1
## 9 mecanico 107.52619 1 0 2 Inf 1 Inf 1
## 10 mecanico 108.46549 0 0 2 Inf 0 Inf 1Respondemos en primer lugar al número de máquinas en funcionamiento al cabo del tiempo simulado. Sabemos que el número de máquinas averiadas en un instante dado será igual al número de reparadores ocupados (server) más el número de máquinas en cola esperando ser reparadas (queue), o lo que es lo mismo, las máquinas que están en el sistema de reparación (system, en resources). Veamos pues, qué ocurre en el último instante en que se ha registrado alguna actividad en el sistema simulado, dado por la última fila en el dataframe de recursos.
# última iteración del sistema
tail(sim.res, 1)## resource time server queue capacity queue_size system limit replication
## 22 mecanico 162.612 0 0 2 Inf 0 Inf 1
# las que están estropeadas
tail(sim.res, 1)$system## [1] 0
# las que están en funcionamiento
4-tail(sim.res, 1)$system## [1] 4Para saber el tiempo que las cuatro máquinas han estado funcionando simultáneamente, identificamos en primer lugar en qué instantes las cuatro estaban operativas (system=0).
# identificamos instantes en que todas las máquinas están operativas
sel=which(sim.res$system==0)
# calculamos todas las secciones de tiempo delimitadas por instantes en que se ha producido alguna actividad, junto con el final del periodo, t
tiempos = diff(c(sim.res$time,t))
# y sumamos las franjas en las que se ha mantenido el evento de interés, pasándolo a porcentaje
sum(tiempos[sel])*100/t## [1] 62.44074Por último buscamos responder la cuestión de cuánto tiempo de funcionamiento se pierde por averías. Para ello calculamos el tiempo total gastado en reparaciones (activity_time en arrivals), más el tiempo de esperas en cola, y lo restamos al tiempo total que deberían haber estado funcionando las máquinas.
# utilizamos la información en las llegadas maquinas.df.arr
# tiempo total gastado en reparaciones (`activity_time`)
t.repara <- sum(sim.arr$activity_time)
# tiempo de esperas en cola
t.cola <- sum(sim.arr$end_time-sim.arr$start_time-sim.arr$activity_time)
# Porcentaje del tiempo total de funcionamiento en que han estado paradas las máquinas
t.sinfun<- (t.repara+t.cola)*100/(4*t)
round(t.sinfun,2)## [1] 3.63Para obtener una estimación y su error habremos de realizar estos cálculos para nreplicas (simulaciones) del sistema durante el periodo de interés.
nreplicas<-500 # réplicas para estimación MC
t=24*7 # tiempo de simulación (en horas)
lambda=1/72; mu=1/2
capacidad=2 # nº reparadores
K=4 # nº máquinas
envs <- mclapply(1:nreplicas, function(i){
mantenimiento(t, lambda,mu, capacidad,K)%>%
wrap()},mc.set.seed=FALSE)
# almacenamos análisis de llegadas del sistema
sim.arr<-as_tibble(get_mon_arrivals(envs))
# almacenamos análisis de recursos del sistema
sim.res<-as_tibble(get_mon_resources(envs))
# y procedemos con los cálculos
# número de máquinas operativas al final
operativas=sim.res %>%
group_by(replication) %>%
summarize(n=4-tail(system,1))
m=mean(operativas$n)
error=sd(operativas$n)/sqrt(nreplicas)
cat("\n Máquinas operativas después de una semana: ",m,"(error=",error,")")##
## Máquinas operativas después de una semana: 3.872 (error= 0.01648562 )
# tiempo en funcionamiento todas las máquinas a la vez
fun.todas = sim.res %>%
group_by(replication) %>%
mutate(dif=diff(c(time,t)),
system0=(system==0)*1) %>%
filter(system0==1) %>%
summarise(tiempos=sum(dif)*100/t)
m=mean(fun.todas$tiempos)
error=sd(fun.todas$tiempos)/sqrt(nreplicas)
cat("\n % Tiempo en que han funcionado simultáneamente todas las máquinas: ",m,"% (error=",error,"%)")##
## % Tiempo en que han funcionado simultáneamente todas las máquinas: 77.98291 % (error= 0.5439864 %)
# tiempo perdido en averías
tpo.averias = sim.arr %>%
group_by(replication) %>%
mutate(parones=end_time-start_time) %>%
summarise(tpo.parones=sum(parones)*100/(4*t))
m=mean(tpo.averias$tpo.parones)
error=sd(tpo.averias$tpo.parones)/sqrt(nreplicas)
cat("\n % Tiempo perdido por averías: ",m,"% (error=",error,"%)")##
## % Tiempo perdido por averías: 2.727233 % (error= 0.04885752 %)4.4.3 Central telefónica
Una centralita telefónica puede atender \(K\) llamadas a la vez en un momento dado. Las llamadas llegan según un proceso de Poisson con tasa \(\lambda\). Si la centralita ya está atendiendo \(K\) llamadas cuando llega una nueva llamada, ésta se pierde. Si una llamada es aceptada, dura un tiempo \(Exp(\mu)\) y luego termina. Todas las llamadas son independientes entre sí. Sea \(X_t\) el número de llamadas que la centralita gestiona en el momento \(t\).
El proceso \(\{X_t; t \geq 0\}\) es una CMTC con espacio de estados \(S = \{0, 1, 2,...,K\}\) de forma que:
En el estado \(i\), con \(0 \leq i \leq K-1\) la llegada de una llamada desencadena una transición al estado \(i+1\) con tasa \(r_{i, i+1} = \lambda\), mientras que en el estado \(K\) no se pueden recibir llamadas, \(\lambda_K=0\).
En el estado \(i\), con \(1 \leq i \leq K\) cualquiera de las llamadas \(i\) puede completarse y desencadenar una transición al estado \(i-1\). La tasa de transición es \(r_{i ,i-1} = i\mu\). En el estado 0 no hay salidas, \(\mu_0=0\).
El sistema \(\{X_t; t \geq 0\}\) es un proceso de nacimiento y muerte con:
\[\begin{eqnarray*} \lambda_i &=& \lambda, \quad 0 \leq i \leq K-1 \\ \mu_i&=& i\mu, \quad 0 < i \leq K, \end{eqnarray*}\]que como veremos más adelante se denomina cola \(M/M/K/K\), es decir, llegadas y servicios exponenciales con \(K\) servidores y de capacidad \(K\).
La función de simmer para estudiar este sistema viene dada por:
# Sistema
#################################################
cola.MMKK <- function(t, lambda, mu, servidores, usuarios)
{
# lambda: tasa de llegadas
# mu: tasa de servicio
# servidores: número de servidores
# usuarios: capacidad total del sistema
cola <- usuarios - servidores
servicio <- trajectory() %>%
seize("atendiendo", amount = 1) %>%
timeout(function() rexp(1, mu)) %>%
release("atendiendo", amount = 1)
# Configuración del sistema
#################################################
simmer() %>%
add_resource("atendiendo", capacity = servidores, queue_size = cola) %>%
add_generator("llegada", servicio, function() rexp(1, lambda)) %>%
run(until = t)
}4.4.4 Call Center
El sistema de reservas telefónicas de una aerolínea es un “call center” formado por \(s\) empleados de reservas llamados agentes. Una llamada entrante para una reserva es atendida por un agente si hay uno disponible; de lo contrario, la persona que llama es puesta en espera. El sistema puede poner en espera a un máximo de \(H\) personas. Cuando un agente está disponible, las llamadas en espera se atienden por orden de llegada. Cuando todos los agentes están ocupados y hay \(H\) llamadas en espera, cualquier llamada adicional recibe una señal de ocupado y se pierde permanentemente. Sea \(X_t\) la variable aleatoria que registra el número de llamadas en el sistema (atendidas y en espera). Si las llamadas entrantes se comportan como un \(PP(\lambda)\) y los tiempos de procesamiento de las llamadas son variables aleatorias iid \(Exp(\mu)\), el sistema \(\{X_t; t \geq 0\}\) es una CMTC con espacio de estados \(S = \{0, 1, 2,...,K\}\), donde \(K = s + H\).
Se puede demostrar fácilmente que este sistema, comúnmente conocido como cola \(M/M/s/K\), es un proceso de nacimiento y muerte con tasas:
\[\begin{eqnarray*} \lambda_i &=& \lambda, \quad 0 \leq i \leq K-1 \\ \mu_i&=& min(i,s) \cdot \mu, \quad 0 < i \leq K, \end{eqnarray*}\]Para simular este proceso podemos utilizar la función del ejemplo anterior.
4.5 Otros tipos de sistemas
Presentamos a continuación otros sistemas que no se corresponden con procesos de nacimiento y muerte, pero que son muy habituales en el mundo real.
4.5.1 Gestión de inventarios
Una tienda minorista gestiona el inventario de un tipo de producto, que denominamos \(P\), de la forma siguiente. Cuando el número de elementos de \(P\) disminuye a un número fijo \(l\), se hace un pedido al fabricante de \(m\) repuestos de \(P\). El pedido tarda un tiempo aleatorio en ser entregado al minorista. Si cuando se entrega el pedido, y una vez incluida la entrega, el inventario es a lo sumo de \(l\), entonces se realiza inmediatamente otro pedido de \(m\) artículos. Supongamos que que los plazos de entrega son variables aleatorias iid \(Exp(\lambda)\) y que la demanda se produce según un \(PP(\mu)\). Las demandas que no pueden ser satisfechas inmediatamente se pierden.
Sea \(X_t\) el número de elementos de \(P\) en stock en el momento \(t\). Obsérvese que el número máximo de elementos de \(P\) en stock es \(K = l + m\), de modo que el espacio de estados es \(S = \{0, 1, 2,...,K\}\).
- En el estado \(0\), las demandas se pierden, y el stock salta a \(m\) cuando se entrega el pedido pendiente actual, por lo que \(r_{0m} = \lambda\).
- En el estado \(i\), \((1 \leq i \leq l)\), hay un pedido pendiente. El estado cambia a \(i-1\) si se produce una demanda (a tasa \(\mu\)) y a \(i + m\) si se entrega el pedido. Por lo tanto, tenemos \(r_{i, i+m} = \lambda\) y \(r_{i, i-1} = \mu\). Finalmente, si \(X_t = i\), con \(l + 1 \leq i \leq K\), no hay pedidos pendientes, y la única transición posible es de \(i\) a \(i- 1\) cuando se produce una demanda. Por lo tanto, \(r_{i, i-1} = \mu\).
El proceso \(X_t, t \geq 0\) definido de esta forma es pues una CMTC.
Si \(m=3\) y \(l=2\), su matriz de tasas viene dada por: \[R= \begin{pmatrix} 0&0&0&\lambda&0&0 \\ \mu&0&0&0&\lambda&0 \\ 0&\mu&0&0&0&\lambda \\ 0&0&\mu&0&0&0\\ 0&0&0&\mu&0&0\\ 0&0&0&0&\mu&0 \end{pmatrix} \] Además, si \(0<i\leq 2\), el tiempo de permanencia en un estado \(i\) es el mínimo de los tiempos en que se recibe un pedido y aparece un cliente, por lo que se distribuye \(Exp(\lambda+\mu)\) y la tasa de permanencia es \(r_i=\lambda+\mu\). Si \(i>2\), entonces \(r_i=\mu\) y \(r_0=\lambda\). La matriz generadora del proceso es:
\[Q= \begin{pmatrix} -\lambda&0&0&\lambda&0&0 \\ \mu&-(\lambda+\mu)&0&0&\lambda&0 \\ 0&\mu&-(\lambda+\mu)&0&0&\lambda \\ 0&0&\mu&-\mu&0&0\\ 0&0&0&\mu&-\mu&0\\ 0&0&0&0&\mu&-\mu \end{pmatrix} \] Tienes un ejemplo incompleto de sistema de inventario en esta web.
4.5.2 Proceso de fabricación
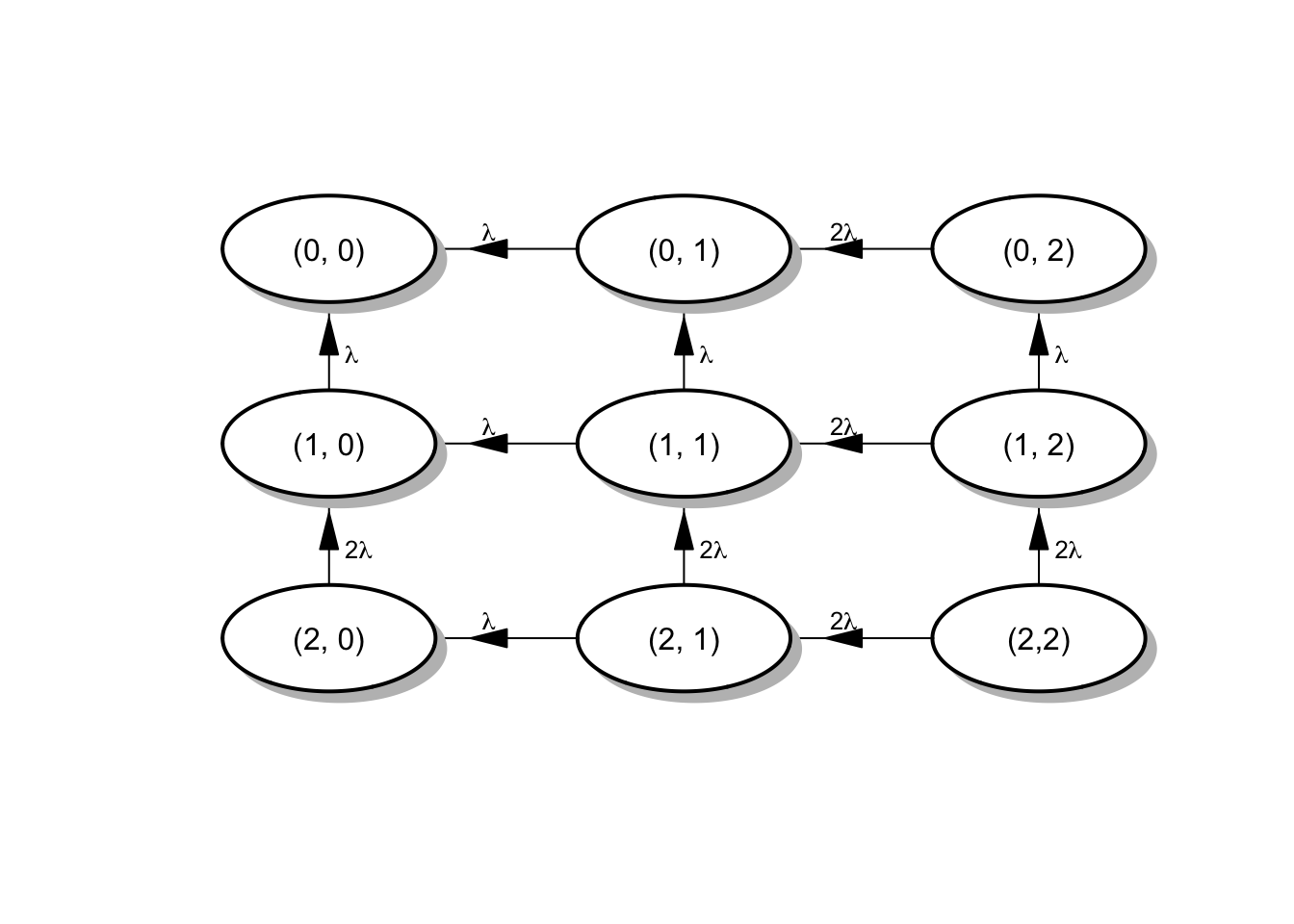
Un proceso de de fabricación sencilla consiste en una sola máquina que puede estar encendida o apagada. Si la máquina está encendida, produce artículos según un proceso de Poisson con tasa \(\lambda\). La demanda de artículos llega según un \(PP(\mu)\). La máquina se controla de la siguiente manera. Si el número de artículos en stock alcanza un número máximo \(K\) (la capacidad máxima del stock), la máquina se apaga. La máquina se enciende cuando el número de artículos en stock disminuye hasta un nivel preestablecido \(l < K\). Si la variable aleatoria \(X_t\) nos indica el número de artículos en stock en el momento \(t\), el proceso \(\{X_t, t \geq 0\}\) no es una CMTC porque no sabemos si la máquina está apagada o encendida cuando \(l < X_t < K\). Si se considera \(Y_t\) como el estado en el que se encuentra la máquina en el momento \(t\), de forma que un \(1\) indica encendido y un \(0\) apagado, entonces el proceso \(\{X_t, Y_t, t\geq 0\}\) con espacio de estados \(S = \{(i, 1), 0 \leq i < K\} \cup \{(i, 0), l < i \leq K\}\) sí que es modelizable como una CMTC.
Hay que tener en cuenta que la máquina siempre está encendida si el número de elementos es \(l\) o menos, por lo que no aparecen los estados \(\{(i, 0), 0 \leq i \leq l\}\). El análisis habitual de los eventos desencadenantes arroja las siguientes tasas de transición:
\[\begin{eqnarray*} r_{(i, 1),(i+1, 1)} &=& \lambda, \quad 0 \leq i < K-1\\ r_{(K-1, 1),(K, 0)}&=& \lambda\\ r_{(i, 1),(i-1, 1)} &=& \mu, \quad 1\leq i\leq K-1\\ r_{(i, 0),(i-1, 0)} &=& \mu, \quad l+1 < i\leq K\\ r_{(l+1, 0),(l, 1)} &=& \mu. \end{eqnarray*}\]4.6 Análisis de transición
El aspecto fundamental para estudiar el comportamiento de cualquier CMTC es la obtención y análisis de la distribución de transición entre los estados del proceso, a partir de la matriz de tasas. Aunque haremos un desarrollo teórico de este problema, veremos que es necesario un algoritmo de computación para obtener dichas probabilidades.
Sea \(X_t, t \geq 0\) una CMTC con espacio de estados \(S = \{1,2,...,N\}\) y con matriz de tasas \(R = (r_{ij})_{i,j \in S}\). Si asumimos que la distribución de probabilidad en el estado inicial, \(X_0\) es conocida, entonces tenemos que la distribución marginal que nos permite predecir la probabilidad de que en un instante dado \(t\) el sistema esté en un estado cualquiera \(j\), viene dada por:
\[Pr[X_t = j] = \sum_{i=1}^N Pr[X_t = j | X_0 = i]\cdot Pr[X_0 = i], \quad 1 \leq j \leq N.\] Es necesario pues para calcularla, obtener la distribución condicionada \(Pr[X_t = j | X_0 = i] = p_{ij}(t)\). Antes de ver cómo obtener dichas probabilidades, introducimos la notación necesaria.
Ya hemos visto antes que una CMTC permanece un tiempo \(Exp(r_i)\) en el estado \(i\) con \(r_i = \sum_{j=1}^N r_{ij}\), y si \(r_i > 0\) entonces pasamos al estado \(j\) con probabilidad \(p_{ij} = r_{ij}/r_i\). Si \(r\) es cualquier número finito mayor o igual que cualquiera de las tasas de permanencia \(r_i\),
\[r \geq max\{r_i, 1\leq i \leq N\}, \quad \] podemos definir la matriz estocástica \(\hat{P} = (\hat{p}_{ij})\) como:
\[\begin{equation} \hat{p}_{ij} = \begin{cases} 1-r_i/r & \text{, si } i=j\\ r_{ij}/r & \text{, si } i \neq j \end{cases} \tag{4.4} \end{equation}\]Teorema 4.2 La matriz de probabilidades de transición \(P(t)=(p_{ij}(t))\) de una CMTC, que contiene las probabilidades de pasar de un estado \(i\) a otro \(j\) en un periodo de amplitud \(t\), viene dada por:
\[\begin{equation} P(t) = \sum_{k=0}^{\infty} e^{-rt}\frac{(rt)^k}{k!} \hat{P}^k \tag{4.5} \end{equation}\] donde \(\hat{P}\) es la matriz definida en la ecuación (4.4).
Esta forma de obtener \(P(t)\) dada en (4.5) se denomina método de uniformización, y proporciona un método numérico para obtener las probabilidades de transición deseadas, sin más que usar los \(m\) primeros términos de la suma infinita definida en (4.5):
\[\begin{equation} P(t)^* = \sum_{k=0}^{m} e^{-rt}\frac{(rt)^k}{k!} \hat{P}^k \tag{4.6} \end{equation}\]Para asegurar la convergencia de la suma finita (4.6), se usan como reglas habituales:
\[m \approx max\{rt + r\sqrt{rt}, 20\},\]
y cuando \(rt\) es pequeño, es más conveniente utilizar el valor de \(r\) más pequeño que es mayor que todas las tasas de permanencia,
\[\begin{equation} r= max\{r_i, 1\leq i \leq N\}. \tag{4.7} \end{equation}\]Con todo, en algunos casos es más conveniente utilizar un valor de \(r\) que sea mayor que el anterior, como \(r=\sum_{i=1}^N r_i\).
Algoritmo de uniformización para obtener \(P\) con una suma finita
- Fijar la matriz de tasas \(R\), el instante de tiempo \(t\), y \(0 < \epsilon < 1\) la tolerancia deseada (máximo error permitido). Por defecto fijamos \(\epsilon=0.00001\).
- Obtener \(r\) con (4.7).
- Calcular \(\hat{P}=Phat\) con la ecuación @ref(eq:phatTransicion}.
- Inicializar \(A = \hat{P}\); \(c = e^{rt}\); \(B = e^{rt}I\); \(sum = c\); \(k=1\).
- Mientras que \(sum <1-\epsilon\), calcular:
c = c*(rt)/k
B = B + cA
A = A * Phat
sum = sum + c
k = k + 1Al finalizar, la matriz \(B\) es una aproximación de \(P(t)\), con error acotado por \(\epsilon \geq \sum_{k=m+1}^{\infty} e^{-rt} \frac{(rt)^k}{k!}\).
En nuestro algoritmo añadiremos un parámetro extra para indicar cómo se debe calcular el valor de \(r\), bien como el máximo o como la suma de las tasas de permanencia.
matriz.prob.trans<- function(Rmat, ts, cal)
{
# Algoritmo de uniformización para obtener P(t)
################################################
# Parámetros de la función
# Rmat: matriz de tasas
# ts: instante de tiempo
# epsilon: error en la aproximación
# cal: forma de obtener r, con dos valores 1 = máximo, 2 = suma finita
epsilon <- 1e-05
# Paso 2. Cálculo de r
ris <- apply(Rmat, 1, sum)
rlimit=ifelse(cal == 1, max(ris), sum(Rmat))
# Paso 3. Cálculo de hat(P)
hatP <- Rmat/rlimit
diag(hatP) <- 1 - ris/rlimit
# Paso 4. Cálculo de matrices y vectores accesorios
rts <- rlimit*ts
A <- hatP
c <- exp(-rts)
B <- c*diag(nrow(Rmat))
suma <- c
k <- 1
# Bucle simulación
while(suma < (1- epsilon))
{
c <- c*rts/k
B <- B + c*A
A <- A%*%hatP
suma <- suma + c
k <- k + 1
}
return(round(B, 4))
}Veamos un ejemplo donde la matriz de tasas viene dada por:
Si estamos interesados en las probabilidades de transición entre estados cuando han transcurrido 2 unidades de tiempo, podemos calcular (ambas versiones):
ts=2
Pmat1<-matriz.prob.trans(R, ts, 1); Pmat1## [,1] [,2] [,3] [,4]
## [1,] 0.2001 0.2001 0.4 0.1998
## [2,] 0.2002 0.2001 0.4 0.1997
## [3,] 0.1999 0.2000 0.4 0.2001
## [4,] 0.1998 0.1999 0.4 0.2003
Pmat2<-matriz.prob.trans(R, ts, 2); Pmat2## [,1] [,2] [,3] [,4]
## [1,] 0.2001 0.2001 0.4 0.1998
## [2,] 0.2002 0.2001 0.4 0.1997
## [3,] 0.1999 0.2000 0.4 0.2001
## [4,] 0.1998 0.1999 0.4 0.2003Ambas matrices proporcionan un resultado prácticamente idéntico. Estas matrices nos permiten obtener las probabilidades de pasar del estado 1 a cualquiera de los otros estados en dos unidades de tiempo, sin más que tomar los elementos de la fila 1 de la matriz obtenida.
Pmat1[1,]; Pmat2[1,]## [1] 0.2001 0.2001 0.4000 0.1998## [1] 0.2001 0.2001 0.4000 0.1998¿Cómo interpretamos esas probabilidades?
Veamos ahora la aplicación de este algoritmo a alguno de los ejemplos con los que hemos trabajado ya en esta unidad.
Ejemplo 4.8 Para los datos correspondientes al cajero bancario en la sección Cajero Bancario, estamos interesados en conocer la probabilidad de que después de 50 minutos de funcionamiento el sistema esté completamente ocupado (1 usuario atendido y tres en cola), sabiendo que en el instante inicial partimos de \(0\) clientes en el sistema. La matriz de tasas viene dada por:
estados <- c(0, 1, 2, 3, 4)
nestados <- length(estados)
R <- matrix(nrow = nestados, ncol = nestados, data = 0)
lambda <- 15/60
mu <- 1/6
R[1,2] <- lambda
R[2,1] <- mu
R[2,3] <- lambda
R[3,2] <- mu
R[3,4] <- lambda
R[4,3] <- mu
R[4,5] <- lambda
R[5,4] <- muQueremos calcular pues, \(P(50)\), y en particular el elemento \(p_{04}(50)\). Obtenemos la distribución de probabilidad asociada al estado 4 para \(t = 50\):
# Matriz de probabilidades de transición
Pmat<-matriz.prob.trans(R, 50, 2)
Pmat## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.0812 0.1190 0.1730 0.2528 0.3741
## [2,] 0.0793 0.1172 0.1722 0.2539 0.3775
## [3,] 0.0769 0.1148 0.1711 0.2553 0.3819
## [4,] 0.0749 0.1128 0.1702 0.2565 0.3856
## [5,] 0.0739 0.1118 0.1698 0.2571 0.3874La probabilidad de interés es 0.3741 (que representa la probabilidad \(p_{04}(50)\)), lo que demuestra que es factible que el sistema llegue al estado 4 partiendo del estado 0 después de 4 horas.
Aunque el cálculo teórico es muy preciso, hay situaciones en que los sistemas reales con los que estamos trabajando hacen bastante costoso obtener la matriz \(R\), y resulta más sencillo tratar de aproximar las probabilidades de transición mediante simulación. Para ello basta con replicar el sistema de simulación un número lo suficientemente grande de veces, y aproximar mediante Monte-Carlo.
En nuestro ejemplo deberíamos simular el estado del sistema durante 50 minutos, replicarlo varias veces y aproximar la probabilidad como el número de réplicas en que se alcanza la ocupación completa del sistema en el instante 50, dividido por el número de réplicas realizadas. La precisión de esta aproximación depende en gran medida del número de réplicas, como siempre en la estimación Monte Carlo. La única puntualización a considerar es que hemos de modificar el algoritmo de simulación para inicializar el sistema en el estado que deseemos. De no hacerlo así, obtendremos resultados dispares. Veamos cuál es el resultado si simulamos sin especificar el estado inicial del que arranca el sistema.
replicas <- 2500
#simulamos SIN especificar el estado inicial
envs <- mclapply(1:nreplicas, function(i){
cola.MM1K(50, 15/60, 1/6, 1, 4)%>%
wrap()},mc.set.seed=FALSE)
# almacenamos el análisis de recursos del sistema
simresource <- as_tibble(get_mon_resources(envs))
# Almacenamos el estado final de la cola en el último instante del sistema
salida <- simresource %>%
group_by(replication) %>%
summarise(estado = last(system))
# Estimamos la probabilidad de acabar en cualquiera de los estados
round(table(salida$estado)/replicas, 3)##
## 0 1 2 3 4
## 0.016 0.023 0.027 0.047 0.086Claramente, la probabilidad estimada es \(Pr(X_{50}=4)\), que es distinta a la pretendida, \(Pr(X_{50}=4|X_0=0)\).
Para practicar la obtención de la matriz de probabilidades de transición puedes resolver los ejercicios B4.1 a B4.4 de la colección al final de la unidad.
4.7 Análisis de tiempos de ocupación
En esta sección, nos centramos en el análisis de los tiempos de ocupación de un estado determinado en un intervalo de tiempo finito \((0, T]\), es decir, el tiempo esperado que el sistema pasa en ese estado. Como ocurre con las probabilidades de transición, presentamos un algoritmo para obtener los tiempos de ocupación a partir de la matriz de tasas, y veremos también cómo la simulación del proceso nos puede ayudar a dar respuesta a las mismas cuestiones.
Teorema 4.3 Si \(P(t)\) es la matriz de probabilidades de transición del proceso \(\{X_t, t \geq 0\}\) con espacio de estados \(S = \{1, 2,...,N\}\), se define la cantidad \(m_{ij}(T)\) como el tiempo de ocupación del estado \(j\) hasta el instante \(T\) partiendo del estado \(i\) como:
\[\begin{equation} m_{ij}(T) = \int_0^T p_{ij}(t)dt, \quad 1 \leq i, j \leq N. \tag{4.8} \end{equation}\]Cuando tenemos formas explícitas para cada uno de los elementos de \(P(t)\), como es el caso para la mayoría de los sistemas de colas de espera, este problema se puede resolver teóricamente. Sin embargo, en la mayoria de ocasiones es necesario un algoritmo de computación para aproximarlos. A continuación se presenta el algoritmo necesario, pero antes veamos la aproximación mediante series de la matriz \(M(T) = (m_{ij}(T))\).
Teorema 4.4 Si \(Y\) es una variable aleatoria Poisson de parámetro \(r\cdot T\), entonces:
\[\begin{equation} M(T) = \frac{1}{r} \sum_{k = 0}^{\infty} Pr(Y > k) \hat{P}^k, \quad T \geq 0. \tag{4.9} \end{equation}\]y se puede aproximar con una suma finita de orden \(m\) utilizando el algoritmo de uniformización a continuación.
Algoritmo de uniformización para obtener \(M(T)\) como una suma finita:
- Fijar \(R\), \(T\), y \(0 < \epsilon < 1\) máximo error tolerable. Por defecto fijamos \(\epsilon = 0.00001\).
- Obtener r.
- Calcular \(\hat{P}\).
- Calcular \(A = \hat{P}\); \(k = 0\)
- Inicializar \(yek = exp(-r*t)\), \(ygk = 1 - yek\), \(suma = ygk\)
- Calcular \(B = ygk * I\)
- Mientras que \(suma/r < T-\epsilon\), calcular:
k = k + 1
yek = yek*(rT)/k
ygk = ygk - yek
B = B + ygk*A
A = A\hat{P}
suma = suma + ygkAl finalizar, la matriz \(B/r\) es una aproximación de \(M(T)\) con error inferior a \(\epsilon\).
En nuestro algoritmo añadiremos un parámetro extra para indicar cómo se debe calcular el valor de \(r\), bien como el máximo o la suma de las tasas de permanencia.
tiempos.ocupacion<- function(Rmat, Ts, cal)
{
# Algortimo de uniformización para obtener M(T)
################################################
# Parámetros de la función
# Rmat: matriz de tasas
# ts: instante de tiempo
# epsilon: error en la aproximación
# cal: forms de obtener r con dos valores 1 = máximo, 2 = suma
epsilon <- 1e-05
# Paso 2. Calculo de r
ris <- apply(Rmat, 1, sum)
rlimit=ifelse(cal == 1, max(ris),sum(Rmat))
# Paso 3. Calculo de hat(P)
hatP <- Rmat/rlimit
diag(hatP) <- 1 - ris/rlimit
# Paso 4.
k <- 0
A <- hatP
# Paso 5.
yek <- exp(-1*rlimit*Ts)
ygk <- 1 - yek
suma <- ygk
# Paso 6.
B <- ygk*diag(nrow(Rmat))
# Bucle simulación
cota <- Ts- epsilon
while(suma/rlimit < cota)
{
k <- k + 1
yek <- yek*(rlimit*Ts)/k
ygk <- ygk - yek
B <- B + ygk*A
A <- A%*%hatP
suma <- suma + ygk
}
return(round(B/rlimit, 4))
}Ejemplo 4.9 Retomando el sistema sobre el tiempo de vida de una máquina descrito en el ejemplo 4.5, supongamos que el tiempo esperado hasta que falla una máquina son 10 días, mientras que el tiempo esperado de reparación es de 1 día. Si la máquina funciona el primer día de enero, ¿cuánto tiempo estará en funcionamiento la máquina al finalizar el mes de enero?
Dado que el proceso (número de máquinas averiadas) sólo tiene espacio de estados \(S = \{0, 1\}\), 0=parada y 1=funcionando, la cantidad de interés es \(m_{11}(31)\). Con \(\lambda = 1\) y \(\mu = 0.1\), la matriz de tasas del proceso viene dada por:
nestados <- 2
estados=as.character(0:1)
lambda <- 1
mu <- 0.1
R <- matrix(nrow = nestados, ncol = nestados, data = 0,dimnames=list(estados,estados))
R[1,2] <- lambda
R[2,1] <- mu Obtenemos ahora la matriz de tiempos de ocupación tras 31 días, \(M(31)\), que nos dará la cantidad de interés; en concreto nos fijaremos en la segunda fila, teniendo en cuenta que partimos de que la máquina está en marcha inicialmente.
ocupacion=tiempos.ocupacion(R, 31, 1)
ocupacion## 0 1
## 0 3.6446 27.3554
## 1 2.7355 28.2645Por tanto, el tiempo esperado de funcionamiento es de 28.3 días, mientras que el tiempo dedicado a reparaciones es de 2.7 días.
Utilizando el simulador del proceso a continuación, sin especificar el estado inicial, obtenemos resultados aproximados, que relacionarán la distribución estacionaria con los tiempos de ocupación. Lo estudiamos a continuación.
# Réplicas del proceso
replicas <- 2500
envs <- mclapply(1:replicas, function(i) {
sistema.1m(31, 1, 1/10) %>%
wrap()},mc.set.seed=FALSE)
# almacenamos análisis de llegadas del sistema
simarrivals <- as_tibble(get_mon_arrivals(envs))
# Almacenamos el estado final de la cola en el último instante del sistema
simarrivals %>%
mutate(tOFF = end_time - start_time) %>%
group_by(replication) %>%
summarise(totalOFF = sum(tOFF)) %>%
ungroup() %>%
summarise(mOFF = mean(totalOFF), mON = 31 - mOFF)## # A tibble: 1 × 2
## mOFF mON
## <dbl> <dbl>
## 1 3.21 27.8Para practicar el cálculo de los tiempos de ocupación puedes resolver los ejercicios B4.5 a B4.8 de la colección al final de la unidad.
4.8 Comportamiento límite del proceso
En el análisis del comportamiento límite de una CMTD analizamos la distribución de probabilidad límite, la distribución estacionaria, y la distribución de los tiempos de ocupación. En el caso de las CMTC estas distribuciones coinciden.
En primer lugar analizamos las probabilidades límite:
\[\lim_{t \rightarrow \infty} Pr[X_t = j], \quad 1 \leq j \leq N.\]
Si existen dichos límites, el vector \(p = (p_1, p_2,...,p_N)\) se conoce como distribución límite de la CMTC.
Teorema 4.5 Una CMTC \(\{X_t, t \geq 0\}\) irreducible con matriz de tasas \(R\) tiene una única distribución límite \(p = (p_1, p_2,...,p_N)\), que se puede obtener como solución de las ecuaciones de balance:
\[\begin{eqnarray} p_j r_j &=& \sum_{i=1}^N p_i r_{ij}, \quad 1 \leq j \leq N \\ \sum_{i=1}^N p_i &=& 1. \nonumber \tag{4.10} \end{eqnarray}\]Podemos interpretar \(p_j r_j\) como la tasa a la que la CMTC deja el estado \(j\), y \(p_i r_{ij}\) como la tasa a la que la CMTC entra al estado \(j\) desde el estado \(i\). Por lo tanto, esta ecuación de balance (4.10) nos dice que las probabilidades límite son tales que la tasa de entrada al estado \(j\) desde todos los estados restantes es igual a la tasa a la cual el sistema deja el estado \(j\), es decir, se produce un balance entre las entradas y las salidas.
Teorema 4.6 Dada una CMTC \(\{X_t, t \geq 0\}\) irreducible con distribución límite \(p\), se tiene que la distribución estacionaria de la CMTC viene dada por \(p\), es decir, \(p_j\) es la probabilidad de que el sistema esté en estado \(j\) en el largo plazo.
La siguiente cuestión es sobre si ocurre en la CMTC lo mismo que ocurría ya en las CMTD con la distribución de ocupación, esto es, si coincidía con la distribución límite y con la distribución estacionaria. La respuesta la tenemos en el siguiente teorema.
Teorema 4.7 Sea \(m_{ij}(T)\) el tiempo total esperado que la cadena permanece en el estado \(j\) hasta el instante \(T\) para una CMTC irreducible que comienza en el estado \(i\). Entonces tenemos la siguiente igualdad que relaciona la distribución límite con la distribución estacionaria dada por \(\{p_j; j \in S\}\):
\[\lim_{T \rightarrow \infty} \frac{m_{ij}(T)}{T} = p_j.\]
Así pues, una CMTC ireducible tiene una única distribución límite, que es también su distribución estacionaria y su distribución de ocupación. Se puede calcular pues, resolviendo las ecuaciones de balance (4.10).
A continuación se presenta la solución de la distribución límite para los procesos de nacimiento y muerte. En el resto de sistemas se deberán plantear las ecuaciones de balance y resorverlas. En ambas situaciones presentamos las correspondientes funciones que nos permiten obtener las cantidades de interés.
Sea \(\{X_t, t \geq 0\}\) un proceso de nacimiento y muerte con espacio de estados \(S = \{0, 1,...,K\}\), y tasas de nacimiento \(\{\lambda_i, 0 \leq i < K\}\) y tasas de muerte \(\{\mu_i, 1 \leq i \leq K\}\). Entonces la CMTC así definida es irreducible y tiene una única distribución límite con:
\[p_i = \frac{\rho_i}{\sum_{j = 0}^K \rho_j}, \quad 0 \leq i \leq K,\] donde \(\rho_0 = 1,\) y
\[\rho_i = \frac{\prod_{j=0}^{i-1}\lambda_j}{\prod_{j=1}^{i}\mu_j}, \quad 1 \leq i \leq K.\]
Antes de comenzar con los ejemplos, vamos a crear una función que permita obtener la distribución límite y la distribución de ocupación para los procesos de nacimiento y muerte.
# Obtención de distribuciones límite
distr.lim.nm <- function(estados, lambdas, mus)
{
# Parámetros de la función
# ========================
# estados: número de estados del sistema (K)
# lambdas: vector de tasas de nacimiento lambda0,..., lambda(K-1)
# mus: vector de tasas de muerte mu1,...,muK
# definimos vector de rho
rhos <- rep(1, estados)
# calculamos productos acumulados para lambda y mu
prl <- cumprod(lambdas)
prm <- cumprod(mus)
# rellenamos rho con los productos acumulados
rhos[2:estados] <- prl/prm
# suma de rhos
sumarhos <- sum(rhos)
# vector de probabilidades
ps <- rhos/sumarhos
return(ps)
}Ejemplo 4.10 Retomando el sistema descrito en el ejemplo 4.5, supongamos que el tiempo esperado hasta que falla una máquina son 10 días, mientras que el tiempo esperado de reparación es de 1 día. ¿Cuál es la distribución límite del proceso y cómo ha de interpretarse?
Este sistema es un proceso de nacimiento y muerte donde podemos aplicar la función anterior para obtener la distribución límite con dos estados y tasas \(\lambda = 1\), \(\mu = 1/10\) (expresadas en días).
lambda=1
mu=0.1
estados=2
probs <- distr.lim.nm(estados,lambda,mu)
probs## [1] 0.09090909 0.90909091El comportamiento límite nos indica que la máquina está el 90.9% del tiempo en funcionamiento, mientras que sólo el 9.1% en reparación. Para un periodo de un año tendríamos que los días esperados de reparación y funcionamiento serían, respectivamente:
round(365*probs)## [1] 33 332Veamos ahora cómo obtener la distribución límite para procesos más generales. Definimos una función que nos permite obtener la distribución límite de un CMTC a partir de cualquier matriz de tasas \(R\), resolviendo las ecuaciones de balance (4.10) matricialmente. Estas ecuaciones equivalen a resolver el sistema:
\[A\cdot p= C\]
donde A es una matriz construida a partir de la traspuesta de la matriz generadora \(Q=R-diag(r)\), con \(r\) un vector con las tasas de permanencia \(r_1,...,r_N\), a la que se le añade en la última fila un vector de unos, y \(C\) es una matriz columna de ceros, con la última fila igual a 1 para introducir la restricción de que los \(p_j\) definen una distribución de probabilidad y suman 1. Esto es,
\[A=\begin{pmatrix} Q' \\ 1 1 ... 1 \end{pmatrix} \]
\[\begin{eqnarray} A \cdot p &=& C \nonumber \\ \begin{pmatrix} -r_1 & r_{21} & ... & r_{N1} \\ r_{12} & -r_2 & ... & r_{N2} \\ . & . & .& \\ r_{1N} & r_{2N} & ... & -r_{N} \\ 1 & 1 & ... & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} p_1 \\ p_2 \\ . \\ p_N \end{pmatrix} &=& \begin{pmatrix} 0 \\ 0 \\ . \\ 1 \end{pmatrix} \end{eqnarray}\]
# Función para la resolución numérica de las ecuaciones de balance
distr.lim.general<-function(Rmat)
{
# Parámetros de la función
#=========================
# Rmat: matriz de tasas del sistema
# número de estados del sistema
estados <- nrow(Rmat)
# Calculamos r_i y lo colocamos en formato matriz
sumarows <- diag(apply(Rmat, 1, sum), estados)
# Matriz de coeficientes del sistema de ecuaciones de balance
A <- t(R)-sumarows
# Completamos la matriz añadiendo la restricción de suma de p`s igual a 1
A <- rbind(A, rep(1, estados))
# Vector de términos independientes del sistema
CS <- c(rep(0, estados), 1)
# Resolución del sistema
ps <- qr.solve(A, CS)
return(ps)
}Ejemplo 4.11 Para el sistema del Proceso de fabricación se está interesado en conocer cuándo la máquina estará parada a largo plazo. Dado que el espacio de estados es \(S = \{1, 2,...,6\}\). La máquina estará parada cuando nos encontremos en los estados \(5 = (4, 0)\) y \(6 = (3, 0)\). A partir de la información del sistema podemos obtener la distribución límite del proceso, pero en este caso, como no se trata de un proceso de nacimiento y muerte debemos plantear las ecuaciones de balance a partir de la matriz de tasas, y resolver el sistema numéricamente con la función distr.lim.general() definida anteriormente.
Resolvemos las ecuaciones de balance para el sistema del proceso de fabricación. Definimos la matriz de tasas y ejecutamos la función anterior para obtener las probabilidades límite del proceso:
# Estados del sistema
nestados <- 6
# Matriz de tasas
lambda <- 6
mu <- 5
R <- matrix(nrow = nestados, ncol = nestados, data = 0)
R[1,2] <- lambda
R[2,1] <- mu
R[2,3] <- lambda
R[3,2] <- mu
R[3,4] <- lambda
R[4,3] <- mu
R[4,5] <- lambda
R[5,6] <- mu
R[6,3] <- mu
# Resolución de las ecuaciones de balance
ps <- distr.lim.general(R)
ps## [1] 0.1584649 0.1901579 0.2281895 0.1244670 0.1493604 0.1493604La probabilidad de interés viene dada por 0.2987, de forma que la máquina permanecerá apagada aproximadamente el 30% del tiempo.
Para practicar con el cálculo de la distribución estacionaria, puedes resolver los ejercicios B4.9 a B4.12 de la colección al final de la unidad.
4.9 Análisis de costes
En este punto vemos cómo podemos introducir costes en las CMTC y los procedimientos numéricos necesarios para su análisis. Seguimos considerando \(\{X_t, t \geq 0\}\) una CMTC con espacio de estados \(S = \{1, 2,...,N\}\) y matriz de tasas \(R\). Además, siempre que la CMTC está en el estado \(i\) se incurre en costes de modo continuo según una tasa \(c(i), 1 \leq i \leq N\).
4.9.1 Coste total esperado hasta \(T\)
Estudiamos en primer lugar el coste total esperado, CTE hasta un instante finito \(T\), llamado horizonte. Nótese que la tasa de coste en el tiempo \(t\) es \(c(X_t)\). Por lo tanto, el coste total hasta el instante \(T\) viene dado por:
\[\int_0^T c(X_t)dt.\]
De esta forma el coste esperado total hasta el instante \(T\), empezando en el estado \(i\), viene dado por:
\[\begin{equation} g(i, T) = E\left[ \int_0^T c(X_t)dt \mid X_0 = i \right], \quad 1 \leq i \leq N. \end{equation}\]
Teorema 4.8 Si \(M(T) = (m_{ij}(T))\) es la matriz de ocupación entonces:
\[\begin{equation} g(T) = M(T) \cdot \begin{pmatrix} c(1) \\ c(2) \\ ... \\ c(N)\end{pmatrix} \end{equation}\]
donde \(c(i)\) representa el coste por permanecer en el estado \(i\) y \(g(T) = [g(1, T), g(2,T),..., g(N-1, T), g(N, T)]'\), donde \(g(i,T)\) representa el coste esperado total hasta el instante \(T\) cuando el sistema se inicia en estado \(i\).
Ejemplo 4.12 Para el sistema de Mantenimiento de máquinas, se sabe que el beneficio por cada hora que la máquina está funcionando es de 50 euros, mientras que el coste de que la máquina este apagada es de 15 euros por hora, al que hay que sumar 10 euros por cada hora de reparación. Estamos interesados en conocer el coste-beneficio de un periodo de 24 horas, si sabemos que al inicio del día todas las máquinas están funcionando.
Si \(X_t\) es el número de máquinas estropeadas en el instante \(t\), el espacio de estados para 4 máquinas viene dado por \(S = \{0, 1, 2, 3, 4\}\) y el vector de costes es:
\[ \begin{matrix} c(4) = & 0\cdot 50 - 4\cdot 15 - 2\cdot 10 = - 80,\\ c(3) = & 1\cdot 50 - 3\cdot 15 - 2\cdot 10 = - 15,\\ c(2) = & 2\cdot 50 - 2\cdot 15 - 2\cdot 10 = 50,\\ c(1) = & 3\cdot 50 - 1\cdot 15 - 1\cdot 10 = 125,\\ c(0) = & 4\cdot 50 - 0\cdot 15 - 0\cdot 10 = 200. \end{matrix} \]
Veamos cómo obtener los costes acumulados en un día utilizando el código correspondiente.
# Matriz de tasas
nestados <- 5
R <- matrix(nrow = nestados, ncol = nestados, data = 0)
lambda <- 1/2
mu <- 1/72
R[1,2] <- 4*lambda
R[2,1] <- mu
R[2,3] <- 3*lambda
R[3,2] <- 2*mu
R[3,4] <- 2*lambda
R[4,3] <- 3*mu
R[4,5] <- lambda
R[5,4] <- 4*mu
# Matriz de ocupación
mmat <- tiempos.ocupacion(R, 24, 1)
# Vector de costes
costes <- matrix(c(200, 125, 50,-15, -80), ncol = 1)
# Matriz de beneficios acumulados
beneficios <- mmat%*%costes
beneficios## [,1]
## [1,] -1242.097
## [2,] -1378.587
## [3,] -1511.844
## [4,] -1638.507
## [5,] -1765.011Luego si se inicia el estado con todas las máquinas funcionando, el coste acumulado tras un día de funcionamiento es de 1242.0975 euros.
4.9.2 Tasas de coste a largo plazo
Para el sistema de Vida útil de una máquina, supongamos que se da el coste \(C\) del tiempo de inactividad. Queremos saber cuál debe ser la tasa de ingresos durante el tiempo de actividad (ingresos percibidos por unidad de tiempo cuando la máquina está operativa), para que sea económicamente rentable operar la máquina. Si nos guiamos por el coste total, la respuesta dependerá del horizonte de planificación \(T\) y también del estado inicial de la máquina. Una alternativa es calcular los ingresos netos a largo plazo por unidad de tiempo para esta máquina e insistir en que sea positivo para la rentabilidad. Esta respuesta no dependerá de \(T\), y como veremos ni siquiera del estado inicial de la máquina. Por lo tanto, el cálculo de estos índices de costes o ingresos a largo plazo es muy útil. En esta subsección mostraremos cómo calcular estas cantidades.
Teorema 4.9 Sea \(\{X_t, t \geq 0\}\) una CMTC irreducible con estados \(\{1, 2,...,N\}\), distribución límite \(p = [p_1, p_2,...,p_N]\) y vector de costes \(c = (c_1, c_2,..., c_N)\), entonces la tasa de coste a largo plazo viene dada por:
\[\begin{equation} g(i) = \sum_{j = 1}^N p_j \cdot c(j), \quad 1 \leq i \leq N. \end{equation}\]
Ejemplo 4.13 Si consideramos el sistema de Vida útil de una máquina, supongamos que cuesta \(C\) que la máquina esté apagada cada unidad de tiempo. ¿Cuál es la tasa mínima de ingresos \(I\) a percibir por cada instante de tiempo que la máquina está operativa, para que el sistema no genere pérdidas (es decir, para alcanzar el punto de equilibrio a largo plazo)?
Utilizando las tasas definidas anteriormente (\(\lambda = 1, \mu = 0.1\)), la distribución límite del sistema \(p = [0.0909, 0.9091]\), y el vector de costes \(c =(-C, I)\) para el espacio de estados \(S = \{0, 1\}\), la tasa de coste a largo plazo por unidad de tiempo viene dada por la expresión:
\[ g = - 0.0909*C+0.9091*I \] de forma que para mantener el sistema en equilibrio, \(g \geq 0\), se debe cumplir que:
\[I \geq \frac{0.0909}{0.9091} \cdot C = 0.099989 \cdot C \approx 0.1 \cdot C\]
Así, obtener unos ingresos por unidad de tiempo operativo superiores a 0.1 veces el coste por unidad de tiempo de que la máquina está parada resulta en pérdidas no negativas.
Verifica si se cumple la condición de equilibrio y cuáles son los beneficios si la empresa ha establecido un ingreso por hora de 50 euros, cuando sabe que el coste por hora es de 10 euros cuando está apagada.
Ejemplo 4.14 Consideramos el sistema de la Central telefónica en que la capacidad máxima de la centralita es de seis llamadas. Las llamadas llegan según un \(PP\) a razón de 4 por minuto, y la duración media de cada llamada es exponencial de media 2 minutos. Consideramos como \(X_t\) al número de llamadas que están siendo atendidas en el instante \(t\).
- Queremos saber el beneficio por unidad de tiempo si la facturación por minuto de cada llamada es de 10 céntimos.
- Queremos estimar la pérdida que sufrimos por todas las llamadas que no pueden ser atendidas.
En primer lugar calculamos la distribución límite del proceso \(X_t\) que representa el número de llamadas en el sistema en un instante \(t\). Dado que se trata de un proceso de nacimiento y muerte, utilizamos la función distr.lim.nm que ya construimos previamente en la sección Comportamiento límite del proceso.
# Matriz de tasas
nestados <- 7
lambdas <- rep(4, 6)
mus <- (1:6)/2
# Probabilidades del sistema
probs <- distr.lim.nm(nestados, lambdas, mus);probs## [1] 0.001070486 0.008563884 0.034255537 0.091348098 0.182696196 0.292313914 0.389751885Establecemos los beneficios por unidad de tiempo para cada uno de los estados, \(c(i) = 10i\), y calculamos el coste global por unidad de tiempo:
# vector de beneficios c(i)
beneficio <- 10*(0:6)
# beneficio por unidad de tiempo
sum(beneficio*probs)## [1] 48.81985El beneficio esperado por unidad de tiempo (minuto) es de 48.82 céntimos.
En términos esperados, si el sistema funcionara según sus medias, esto es, a razón de 4 llamadas por minuto, 4, y la duración media de cada llamada, 2 minutos, tendríamos que el beneficio medio esperado por minuto sería de 80 céntimos. Esto implica que el sistema está funcionando por debajo de su capacidad debido a las llamadas que se rechazan, lo que genera unas pérdidas de \(80 - 48.82 = 31.18\) céntimos por minuto.
4.10 Tiempos de primer paso
Como ocurría con las CMTD podemos hablar de los tiempos de primer paso en las CMTC. Si \(\{X_t, t \geq 0\}\) es una CMTC con espacio de estados \(\{1, 2,...,N\}\) y matriz de tasas \(R\), entonces se define como el tiempo de primer paso por el estado \(N\) como:
\[T = min\{t \geq 0: X_t = N\}.\]
Más concretamente estudiamos el valor esperado de \(T\), \(E(T)\). Para ello definimos los tiempos esperados a partir de cada uno de los estados del sistema como:
\[m_i = E(T \mid X_0 = i), \quad 1 \leq i \leq N-1; \qquad m_N = 0.\]
Teorema 4.10 Los tiempos de primer paso por el estado \(N\) cuando el sistema se inicia en el estado \(i\), \(\{m_i, 1 \leq i \leq N-1\}\), satisfacen:
\[r_i \cdot m_i = 1 + \sum_{j=1}^{N-1} r_{ij} \cdot m_j, \quad 1\leq i \leq N-1.\]
Si deseamos calcular los tiempos de primer paso por un subconjunto de estados \(A\), el teorema anterior se adapta según:
\[r_i \cdot m_i(A) = 1 + \sum_{j \notin A} r_{ij} \cdot m_j(A), \quad 1\leq i \leq N-1.\]
A continuación presentamos un algoritmo para calcular los valores de \(m_i\) a partir de la matriz de tasas del sistema, donde debemos indicar el estado o estados para los que queremos calcular el tiempo hasta el primer paso.
# Función para la resolución numérica de los tiempos de primer paso en cmtc
tiempos.primer.paso<-function(Rmat, A, estados)
{
# Parámetros de la función
#=========================
# Rmat: matriz de tasas del sistema
# A: vector de estados que queremos alcanzar
# estados: conjunto de estados total (como carácter)
# Estados como texto
estados <- as.character(estados)
# Tasas r
rts <- diag(apply(Rmat, 1, sum), nrow(Rmat))
# Seleccionamos el subconjunto de la matriz quitando fila y columna
Rmod <- Rmat[-A, -A]
rates <- rts[-A, -A]
# Número de m´s a estimar
lms <- nrow(Rmod)
# Matriz de coeficientes del sistema de ecuaciones de balance
B <- rates - Rmod
# Vector de términos independientes del sistema
CS <- rep(1, lms)
# Resolución del sistema
ps <- as.data.frame(qr.solve(B, CS))
rownames(ps) <- paste("estado", estados)[-A]
colnames(ps) <-"tiempo"
return(ps)
}Ejemplo 4.15 En las condiciones del sistema \(M/M/1/K\) del Cajero Bancario descrito anteriormente, estamos interesados en conocer el tiempo que debe transcurrir hasta que la cola esté vacía, si ahora mismo hay un cliente en el sistema y cero en la cola (\(X_0 = 1\)). Recordemos que el espacio de estados hace referencia al número de clientes en la cola y viene dado por \(\{0, 1, 2, 3, 4, 5\}.\)
# Definición matriz de tasas
nestados <- 6
R <- matrix(nrow = nestados, ncol = nestados, data = 0)
R[1,2] <- 10
R[2,1] <- 15
R[2,3] <- 10
R[3,2] <- 15
R[3,4] <- 10
R[4,3] <- 15
R[4,5] <- 10
R[5,4] <- 15
R[5,6] <- 10
R[6,5] <- 15
# Tiempos de primer paso el estado 1 (0 clientes en el sistema) que deseamos alcanzar (corresponde con el primer elemento del espacio de estados)
tiempos.primer.paso(R, 1, 0:5)## tiempo
## estado 1 0.1736626
## estado 2 0.3341564
## estado 3 0.4748971
## estado 4 0.5860082
## estado 5 0.6526749El tiempo esperado hasta que la cola esté vacía de nuevo es de 0.1736 horas, o lo que es lo mismo, 10.42 minutos.
Ejemplo 4.16 En las condiciones del sistema de Mantenimiento de aronaves descrito anteriormente. Supongamos que en un experimento de prueba, el avión despega con cuatro motores que funcionan correctamente y sigue volando hasta que se estrella. Estamos interesados en conocer el tiempo esperado hasta el primer accidente.
El espacio de estados del sistema es \(\{1, 2,...,,9\}\), y sabemos que el avión se estrellará si en algún momento accedemos al subconjunto de estados \(\{1, 2, 3, 4, 7\}\). Calculamos los tiempos de primer paso cuando \(X_0 = \{5, 6, 8, 9\}\), aunque como el avión está en condiciones óptimas para despegar nos debemos fijar en el valor correspondiente al estado 9. Recordemos que el tiempo medio hasta que falla un motor es de 200 horas, de forma que \(\lambda = 1/200 = 0.005\).
# Definición matriz de tasas
nestados <- 9
lambda <- 0.005
R <- matrix(nrow = nestados, ncol = nestados, data = 0)
R[2,1] <- lambda
R[3,2] <- 2*lambda
R[4,1] <- lambda
R[5,2] <- lambda
R[5,4] <- lambda
R[6,3] <- lambda
R[6,5] <- 2*lambda
R[7,4] <- 2*lambda
R[8,5] <- 2*lambda
R[8,7] <- lambda
R[9,6] <- 2*lambda
R[9,8] <- 2*lambda
# Conjunto que debemos alcanzar
A <- c(1, 2, 3, 4, 7)
# Tiempos de primer paso
tiempos.primer.paso(R, A, 1:9)## tiempo
## estado 5 100.0000
## estado 6 133.3333
## estado 8 133.3333
## estado 9 183.3333De esta forma, si el avión parte en condiciones óptimas (estado 9) el tiempo hasta que ocurra un accidente que le impida volar es de 183.33 horas, o lo que es lo mismo 183 horas y 20 minutos.
4.11 Ejercicios
4.11.1 Básicos
Ejercicio B4.1. Para el proceso de Mantenimiento de máquinas estamos interesados en calcular el valor esperado del número de máquinas en funcionamiento después de 9 horas de funcionamiento, suponiendo que el sistema empieza con todas las máquinas paradas.
Ejercicio B4.2. Para el proceso de Mantenimiento de aronaves supongamos que cada motor funciona en promedio unas 200h antes de detectarse cualquier problema. Si los cuatro motores están funcionando antes de comenzar un vuelo de seis horas, ¿cuál es la probabilidad de que el vuelo llegue de forma segura? (Ayuda: Para resolver este ejercico ten en cuenta la codificación de estados establecida en la definición del sistema).
Ejercicio B4,3. Para el proceso de Central telefónica supongamos que la capacidad total de la centralita es de 10 llamadas y que se reciben llamadas a una tasa de 1 por minuto, y que el tiempo medio de atención de cada llamada es de 10 minutos. Si ahora mismo la centralita está atendiendo a 3 llamadas:
- ¿Cuál es la probabilidad de que la centralita esté como máximo al 50% de su capacidad dentro de media hora? ¿Y dentro de una hora?
- Si la centralita está activa durante 6 horas más, ¿cuántas llamadas estarán pendientes al finalizar el tiempo de trabajo?
Ejercicio B4.4. Para el proceso de Gestión de inventarios supongamos que la capacidad máxima de stock del producto \(KD\) es 20, y que se solicitan nuevas piezas cuando el stock es inferior a 6. Además tenemos que la tasa de entrega de nuevos productos es de tres días, mientras que la demanda de dicho producto es de 3 piezas/dia.
- Si en estos momentos no hay stock de la pieza \(KD\), la empresa está interesada en saber cuál es el stock más probable dentro de 8 días.
- ¿Cuál es la probabilidad de que tenga que reabastecerse en esa fecha?
Ejercicio B4.5. Para el proceso \(M/M/1/K\) del Cajero Bancario supongamos que los clientes llegan con una tasa de 10 por hora y que tardan en promedio unos cuatro minutos en realizar las operaciones con el cajero. Supongamos que hay espacio para una cola de cinco clientes mientras un cliente está siendo atendido. Si el cajero está inactivo ahora mismo, ¿cuánto tiempo permanecerá inactivo durante la próxima hora?
Ejercicio B4.6. Para el Proceso de fabricación consideramos la situación siguiente. Supongamos que el sistema funciona las 24 horas del día, las demandas se producen a cinco por hora y el tiempo medio de fabricación de un artículo es de 10 minutos. La máquina se pone en marcha cuando el stock de artículos fabricados se reduce a dos, y permanece encendida hasta que las existencias aumentan a cuatro, momento en el que se apaga. Supongamos que el stock es de cuatro (y la máquina está apagada) al principio. Estamos interesados en cuánto tiempo estará la máquina está encendida durante las siguientes 24 horas.
Ejercicio B4.7. Para el proceso de Gestión de inventarios supongamos que la capacidad máxima de stock del producto \(KD\) es 20, y que se solicitan nuevas piezas cuando el stock es inferior a 6. Además tenemos que la tasa de entrega de nuevos productos es de tres días, mientras que la demanda de dicho producto es de 3 piezas/dia. Si en estos momentos no hay stock de la pieza \(KD\), la empresa esta interesada en saber cuánto tiempo tardará en tener que reabastecerse durante los próximos 8 días.
Ejercicio B4.8. Para el proceso de Central telefónica supongamos que la capacidad total de la centralita es de 10 llamadas y que se reciben llamadas a una tasa de 1 por minuto, y que el tiempo medio de atención de cada llamada es de 10 minutos.
- Si ahora mismo la centralita está atendiendo a 3 llamadas, ¿cuál es el tiempo esperado de que el sistema esté por encima del 80% de ocupación?
- ¿Y por debajo del 20%?
- ¿Cuánto tiempo el sistema estará a plena capacidad?
Ejercicio B4.9. Para el sistema de Mantenimiento de máquinas consideramos cuatro máquinas disponibles y dos operarios para repararlas en caso de fallo, con tiempos de vida de las máquinas exponenciales con media de 3 días, y tiempos medios de reparación de 2 horas. Estamos interesados en:
- la probabilidad a largo plazo de que todas las máquinas estén en funcionamiento,
- la fracción de tiempo a largo plazo que los dos operarios están ocupados.
Ejercicio B4.10. Para el proceso \(M/M/1/K\) del Cajero Bancario supongamos que los clientes llegan con una tasa de 10 por hora y que tardan en promedio unos cuatro minutos en realizar las operaciones con el cajero. Supongamos que hay espacio como máximo para cinco clientes en cola mientras que un cliente está siendo atendido.
- ¿Cuál es la probabilidad de que tengamos más de dos clientes en la cola?
- ¿Y de que tengamos como máximo 2?
- ¿Cómo interpretamos estas probabilidades?
Ejercicio B4.11. Para el sistema de Mantenimiento de aronaves estamos interesados en conocer cuál es la probabilidad de que el avión no pueda finalizar el vuelo.
Ejercicio B4.12. Para el sistema del Sistema del viajante estamos interesados en saber cuánto tiempo permanecerá en cada ciudad (en términos porcentuales y a largo plazo). En este caso la matriz de tasas debe tener en cuenta las probabilidades de moverse de una ciudad a otra. Si el beneficio que obtiene el vendedor es de 80 euros/día en la ciudad A, 100 euros/día en la ciudad B, 125 euros/día en C, y que además se incurre en un gasto por desplazamiento de 25 céntimos por kilómetro cuando hay 50 kilómetros entre A y B, 65 kilómetros entre A y C, y 80 kilómetros entre B y C.
- ¿Cuál es el beneficio total esperado del sistema para un periodo de un mes?
- ¿Cuál es el beneficio/coste diario a largo plazo?
- Si el viajante comienza su viaje en la ciudad A ¿cuánto tiempo transcurrirá hasta que el viajante vuelva a esa ciudad?
Ejercicio B4.13. Un taller mecánico tiene dos taladradoras y dos tornos. Los tiempos de vida de las taladradoras son v.a. \(Exp(\mu_a)\) y las de los tornos \(Exp(\mu_o)\). El taller mecánico tiene dos reparadores: Alberto y Roberto. Alberto puede reparar tanto tornos como taladros, mientras que Roberto sólo puede reparar tornos. Los tiempos de reparación de las taladradoras son \(Exp(\lambda_a)\) y para los tornos \(Exp(\lambda_o)\), independientemente de quién repare las máquinas. Las taladradoras tienen prioridad en las reparaciones. Las reparaciones pueden adelantarse. Haciendo las suposiciones de independencia apropiadas, modelar este taller mecánico como un CMTC, considerando el proceso \(A(t) = (a, o)\) que indica el número de taladros y tornos en funcionamiento en el instante \(t\) y obtener la correspondiente matriz de tasas.
4.11.2 Avanzados
Ejercicio A4.1 Un fondo de inversión se clasifica en cuatro estados según los beneficios que produce por unidad de tiempo: altos, medios, bajos, y pérdidas. Además, el movimiento entre estados puede ser visto como una CMTC con matriz de tasas:
\[R = \begin{pmatrix} 0 & 0.1 & 0.1 & 0\\ 0 & 0 & 0.3 & 0.1\\ 0 & 0 & 0.5 & 0.5\\ 1.5 & 0 & 0 & 0 \end{pmatrix}\]
Mientras que el sistema está en cada uno de los estados, el beneficio respectivo estimado es de 500, 250, 100, y -600 euros por unidad de tiempo.
- ¿Cuál es el coste total esperado para un periodo de 10 unidades de tiempo?
- ¿Cuál será la tasa de coste a largo plazo?
- Si ahora mismo estamos en pérdidas, ¿cuánto tiempo tiene que pasar hasta que alcanzemos beneficios altos?
- La empresa considera que si el coste del estado de pérdidas se duplicara, esto es, pasara de 600 a 1200, mejorarían los datos de las cuestiones anteriores. ¿Qué le podemos decir a la empresa?
Ejercicio A4.2. Sea \(\{X_t, t \geq 0\}\) una CMTC con estados \(\{1, 2, 3, 4, 5\}\) y matriz de tasas
\[ R = \begin{pmatrix} 0 & 4 & 4 & 0 & 0\\ 5 & 0 & 5 & 5 & 0\\ 5 & 5 & 0 & 4 & 4\\ 0 & 5 & 5 & 0 & 4\\ 0 & 0& 5& 5& 0 \end{pmatrix} \]
- Calcular la matriz de tiempos de ocupación para \(t=0.2\).
- Obtener la distribución límite del proceso.
- Si el sistema incurre en costes de acuerdo a la ecuación \(c(i) = 2i+1, \quad 1\leq i\leq 5\), ¿cuál es el coste total esperado acumulado en 10 unidades de tiempo, si el sistema está ahora mismo en el estado 2?
- ¿Cuál sería la tasa de coste a largo plazo?
- ¿Cuál es el tiempo esperado para pasar del estado 1 al estado 5?
Ejercicio A4.3. Sea \(\{X_t, t \geq 0\}\) una CMTC con estados \(\{1, 2, 3, 4, 5, 6\}\) y matriz de tasas
\[ R = \begin{pmatrix} 0 & 6 & 6 & 8 & 0 & 0\\ 0 & 0 & 6 & 8 & 0 & 0\\ 0 & 0 & 0 & 6 & 4 & 0\\ 0 & 6 & 8 & 0 & 0 & 0\\ 6 & 0& 0& 0& 6 & 0 \end{pmatrix} \]
- Calcular la matriz de tiempos de ocupación para \(t=0.1\).
- Obtener la distribución límite del proceso.
- Si el sistema incurre en costes de acuerdo a la ecuación \(c(i) = 2i^2+3, \quad 1\leq i\leq 6\), ¿cuál el coste total esperado en el intervalo de tiempo \([0, 15]\), si el sistema está ahora mismo en el estado 4?
- ¿Cuál sería la tasa de coste a largo plazo?
- ¿Cuál es el tiempo esperado para pasar del estado 6 al estado 4?
Ejercicio A4.4. Un peso de \(18\) toneladas está sostenido por \(3\) cables que se reparten la carga por igual. Cuando uno de los cables se rompe, los restantes que no se han roto, se reparten la carga a partes iguales. Cuando se rompe el último cable, se produce un fallo. La tasa de fallos de un cable es \(0.2\) por año y tonelada. Los tiempos de vida de los \(3\) cables son independientes entre sí. Se considera \(X_t\) como el número de cables que siguen sin romperse en el momento \(t\).
- ¿Cuál es la probabilidad de que el sistema no falle en dos años?
- ¿Cuánto tiempo tardará el sistema en fallar si ahora los tres cables están bien?
Ejercicio A4.5. Un ordenador tiene cinco unidades de procesamiento (CPUs). Los tiempos de vida de las CUPs son v.a. iid exponenciales de media 2 años. Cuando una CPU falla, el ordenador intenta aislarla automáticamente y reconfigurar el sistema con las demás CPU. Sin embargo, este proceso tiene éxito con una probabilidad \(0.94\), denominada factor de cobertura. Si la reconfiguración tiene éxito, el sistema continúa con una CPU menos. Si el proceso falla, todo el sistema se bloquea. Supongamos que el proceso de reconfiguración es instantáneo y que una vez que el sistema se bloquea, se detiene definitivamente. Se considera \(X_t\) igual a cero si el sistema ha dejado de funcionar en el instante \(t\), o en caso contrario es igual al número de CPUs en funcionamiento en el momento \(t\).
- Si todos los procesadores están en funcionamiento en el instante inicial, ¿cuál es la probabilidad de que los cinco procesadores funcionen 5 años sin fallos?
Imaginemos ahora que el sistema puede ser reparado cuando falla. El tiempo necesario para la reparación es una variable aleatoria exponencial de media 5 días, y una vez se finaliza, todas las CPUS funcionan de nuevo.
- ¿Cuál es la probabilidad de que el sistema este en reparación?.
- ¿Cuánto tiempo tardará el sistema en fallar si en estos momentos funcionan todos los procesadores?
- Supongamos que cada hora de trabajo de cada procesador proporciona 100 euros de beneficio, mientras que las reparaciones cuestan 200 euros/hora. ¿Cuál es el beneficio esperado durante el primer año si los cinco procesadores están trabajndo ahora mismo?
Ejercicio A4.6. Una estación de servicio tiene tres servidores (1, 2 y 3). Cuando llega un cliente, es asignado al servidor libre con el índice más bajo. Si los servidores están ocupados, el cliente no se detiene y deja la estación de servicio. Los tiempos de servicio de cada servidor son v.a. \(Exp(\mu_i)\) con:
- media de 8 minutos para el servidor 1,
- la media del servidor 2 es dos veces mayor que la del servidor 3,
- la media del servidor 1 es dos veces mayor que la del servidor 2.
Los clientes llegan de acuerdo a un \(PP(\lambda)\) con tasa de 20 clientes por hora.
- ¿Cuál es la probabilidad de que los tres servidores estén ocupados a los 20 minutos, asumiendo que el sistema está vacio en el instante 0?
- ¿Cuál es el tiempo de ocupación de cada estado del sistema en 50 minutos, asumiendo que el sistema está vacio en el instante 0?
- ¿Cuál es el tiempo esperado hasta que los tres servidores estén libres, asumiendo que el sistema tiene un cliente?
- Si los costes de los tres servidores son 40, 20 y 10 euros por hora respectivamente, ¿cuál es el valor de \(c\) más pequeño que hace que el sistema sea rentable a largo plazo?
Ejercicio A4.7. Una estación de servicio monoservicio atiende a dos tipos de clientes. Los clientes de tipo \(i, i = 1, 2,\) llegan según un \(PP(\lambda_i)\) independientes. La estación tiene espacio para atender como máximo a \(K\) clientes. Los tiempos de servicio son variables aleatorias iid \(Exp(\mu)\) para ambos tipos de clientes. La política de admisión es la siguiente: si en el momento de una llegada, el número total de clientes en el sistema es \(M\) o menos (\(M < K\) es un número entero fijo), se permite que el cliente que llega se incorpore a la cola; en caso contrario sólo si es del tipo 1. Esto crea un trato preferente para los clientes de tipo 1. Sea \(X_t\) el número de clientes (de ambos tipos) en el sistema en el instante \(t\).Las tasas de llegadas son de 5 minutos, la tasa de servicio de 4 minutos, \(K = 5\) y \(M = 3\).
- ¿Cuál es la variable de interés del sistema?
- ¿Cuáles son los tiempos de ocupación en el periodo de 60 minutos desde el inicio del servicio, si en el instante inicial no hay clientes? ¿Cómo se interpretan?
- ¿Cuál es la probabilidad a largo plazo de que la estación esté vacía?
- Si al abrir la gasolinera tenemos un cliente, ¿cuánto tiempo debe pasar hasta que rechacemos el primer cliente?
Ejercicio A4.8 Una pequeña gasolinera tiene un surtidor y espacio para un total de tres coches (uno en el en el surtidor y dos en espera). El tiempo entre las llegadas de los coches a la estación es una v.a. exponencial con una tasa media de llegada de 10 coches por hora. El tiempo que cada coche pasa delante del surtidor es una variable aleatoria exponencial con una media de cinco minutos (es decir, una tasa media de 12 por hora). Si hay tres coches en la estación y llega otro coche, el coche recién llegado sigue su camino y nunca entra en la estación. Considera \(X_t\) como el número de coches en la estación en el momento \(t\).
- ¿Cuál es la probabilidad a largo plazo de que la estación esté vacía?
- ¿Cuál es el número esperado de coches en la estación a largo plazo?
- ¿Cuál es la proporción de tiempo que la estación estará al completo en un periodo de 8 horas?
- Si al abrir la gasolinera tenemos un cliente, ¿cuánto tiempo debe pasar hasta que no tengamos ningún cliente en el sistema? ¿Y más de uno?
Ejercicio A4.9 (Cola \(M^x/M/1/K\)). Una pequeña tienda de autoservicio 24 horas de carretera tiene espacio para 5 automóviles en el parking. Los vehículos llegan al azar, siendo los tiempos de llegada una v.a. exponencial con una media de 10 vehículos por hora. El número de personas dentro de cada coche es una variable aleatoria, \(N\), donde \(P(N = 1) = 0.1\), \(P(N = 2) = 0.7\) y \(P(N = 3) = 0.2\). La gente de los coches entra en la tienda y permanece en ella un tiempo exponencial. La duración media de la estancia en la tienda es de 10 minutos y cada persona actúa de forma independiente a todas las demás, saliendo de la tienda por separado y esperando en sus coches a los demás. Si llega un coche y la tienda está demasiado llena para que todas las personas del coche entren en ella, el coche saldrá y nadie de ese coche entrará en la tienda.
- Si \(X_t\) es el número de individuos en la tienda en el momento \(t\), obtén la matriz de tasas correspondiente a este proceso.
- ¿Cuál es la probabilidad a largo plazo de que la tienda esté vacía?
- ¿Cuál es la proporción de tiempo que la estación estará completa en un periodo de 24 horas?
Ejercicio A4.10. Un determinado equipo electrónico tiene dos componentes A y B. El tiempo hasta fallo del componente A está descrito por una función de distribución exponencial con un tiempo medio de 100 horas. El componente B tiene una vida media hasta el fallo de 200 horas y también está descrito por una distribución exponencial. Cuando uno de los componentes falla, el equipo se apaga y se realiza el mantenimiento. El tiempo de reparación del componente se distribuye exponencialmente con un tiempo medio de 5 horas si fue A el que falló y 4 horas si es B el que falla. Se considera el proceso \(X_t\) con espacio de estados \(\{1, 2, 3\}\) donde el estado \(1\) denota que el equipo está funcionando, \(2\) denota que el componente A ha fallado, y \(3\) denota que el componente B ha fallado.
- ¿Cuál es la probabilidad a largo plazo de que el equipo funcione?
- ¿Cuál es la proporción de tiempo esperado que el sistema estará funcionando durante las próximas 500 horas?
- Un contratista externo realiza los trabajos de reparación de los componentes cuando se produce un fallo y cobra 100 euros por hora por el tiempo más los gastos de viaje, lo que supone 500 euros más por cada visita. La empresa ha determinado que puede contratar y formar a su propio propio reparador. Si cuentan con su propio empleado para las reparaciones, les costará 40 euros por hora, tanto cuando la máquina esté en funcionamiento como cuando esté parada. Ignorando el coste de la formación inicial y la posibilidad de que un empleado contratado para los trabajos de reparación pueda hacer otras cosas mientras la máquina está en funcionamiento, ¿merece la pena económicamente contratar y formar a su propio personal?
Ejercicio A4.11. Una pieza de automóvil necesita tres operaciones de mecanizado realizadas en una determinada secuencia. Estas operaciones son realizadas por tres máquinas. La pieza se introduce en la primera máquina, donde la operación de mecanizado dura en media 1 minuto. Una vez finalizada la operación, la pieza pasa a la máquina 2, donde el mecanizado requiere un tiempo medio de 1.2 minutos. A continuación, pasa a la máquina 3, donde la operación dura en promedio 1 minuto. No hay espacio de almacenamiento entre las dos máquinas, por tanto si la máquina 2 esta trabajando, la pieza de la máquina 1 no puede ser retirada aunque la operación en la máquina 1 se haya completado. Decimos que la máquina 1 está bloqueada en este caso. Hay un amplio suministro de piezas sin procesar disponibles, de modo que la máquina 1 siempre puede procesar una nueva pieza cuando una pieza terminada se desplaza a la máquina 2.
- Modelar este sistema como una CMTC. (Ayuda: Tener en cuenta que la máquina 1 puede trabajar o estar bloqueada, la máquina 2 puede estar trabajando, bloqueada o inactiva, y la máquina 3 puede estar trabajando o inactiva).
- Calcular la cantidad de tiempo esperada que la máquina 1 está bloqueada durante la primera hora, asumiendo que todas la máquinas están trabajando en el instante inicial.
- Calcular la fracción de tiempo a largo plazo en que la última máquina está trabajando en el sistema de producción.
- Cada máquina cuesta 40 euros por hora mientras trabaja en un componente, y produce un beneficio de 75 euros/hora a la pieza en la que trabaja. El valor añadido, o el coste de funcionamiento, es cero cuando la máquina está parada o bloqueada. Calcula la contribución neta de las tres máquinas por unidad de tiempo a largo plazo.