Unidad 2 Cadenas de Markov de Tiempo Discreto

En esta unidad trabajamos con un tipo especial de proceso estocástico de tiempo discreto: las Cadenas de Markov de Tiempo Discreto, a las que aludiremos en adelante como CMTD. Analizamos teóricamente este tipo de procesos y presentamos las herramientas de cálculo y simulación necesarias para poder resolver problemas asociados a sistemas reales modelizables con una CMTD. Utilizaremos en R la librería markovchain.²⁹

2.1 Definiciones

Definición 2.1 Un proceso estocástico \(\{X(t), t \in \mathbb{N}^*\}\), con \(\mathbb{N}^*\) el conjunto de todos los números naturales incluido el cero, y con espacio de estados de tipo discreto, \(S\), se denomina Cadena de Markov de Tiempo Discreto, si para cualquier par de estados \(i\) y \(j\) de \(S\) se verifica la propiedad de Markov, esto es, que la probabilidad de que el proceso en un instante \(t+1\) se encuentre en un estado \(j\), dado su comportamiento previo, sólo depende del estado en el que el sistema se encontraba justamente en el instante anterior \(t\), esto es, \(X(t)=i\), y no del estado del proceso en los instantes anteriores \(t-1, t-2,...,0\):

\[\begin{eqnarray} &Pr(X(t+1) = j | X(t) = i, X(t-1),...,X(0)) = \nonumber \\ &= Pr(X(t+1) = j | X(t) = i), \tag{2.1} \end{eqnarray}\]

Utilizaremos indistintamente la siguiente notación:

\[\{X(n), n \in \mathbb{N}^*\}\equiv \{X_n, n \geq 0\}\]

La probabilidad condicionada dada en (2.1) se denomina probabilidad de transición de un paso y se denota por \(p_{ij}(t,t+1)\), y es la probabilidad de que, dado que el proceso en el instante \(t\) está en el estado \(i\), un instante más tarde, \(t+1\) haya cambiado al estado \(j\):

\[p_{ij}(t,t+1)=Pr(X(t+1) = j | X(t) = i).\]

De forma similar podemos definir la probabilidad de transición de \(n\) pasos, \(p_{ij}(t,t+n)\) como la probabilidad de que, dado que el proceso en el instante \(t\) está en el estado \(i\), \(n\) instantes más tarde, \(t+n\), esté en el estado \(j\) :

\[\begin{equation} p_{ij}(t,t+n)=Pr(X(t+n) = j | X(t) = i). \tag{2.2} \end{equation}\]

Las probabilidades de transición así definidas cumplen que:

\[\begin{eqnarray*} 0 \leq p_{ij}(t,t+n) &\leq & 1 \\ \sum_{j \in S} p_{ij}(t,t+n) &=& 1, \quad n\geq 1. \end{eqnarray*}\]

Definición 2.2 Una \(CMTD\) dada por \(\{X(t), t \in \mathbb{N}\}\) es homogénea cuando tiene probabilidades de transición estacionarias, es decir, cuando \(p_{ij}(t, t+n)\) no depende de \(t\), es decir, la probabilidad de cambiar del estado \(i\) al estado \(j\) en \(n\) pasos es independiente del instante temporal en que se encuentre el proceso:

\[\begin{equation*} p_{ij}(t, t+n) = p_{ij}(s, s+n). \end{equation*}\]

En este curso sólo estudiaremos \(CMTD\) homogéneas, por lo que para simplificar la notación, a partir de ahora las denotaremos como \(p_{ij}(n)\) a las probabilidades de transición de \(n\) pasos y \(p_{ij}\) a las probabilidades de transición de un paso: \[\begin{eqnarray*} p_{ij} &=& Pr[X(t+1) = j | X(t) = i] \\ p_{ij}(n) &=& Pr[X(t+n) = j | X(t) = i]. \end{eqnarray*}\]

Definición 2.3 El comportamiento aleatorio de una \(CMTD\) está completamente determinado por las probabilidades de transición de la cadena y la distribución del estado inicial, de forma que la función de distribución del proceso en un instante de tiempo \(t\) se calcula, mediante el teorema de la probabilidad total, según la Ecuación (2.3).

\[\begin{equation} Pr[X(t)= k] = \sum_{i \in S} p_{ik}(t) p_i(0), \tag{2.3} \end{equation}\]

con \(p_i(0) = Pr(X(0) = i)\) la probabilidad de que en el instante inicial el proceso se encuentre en el estado \(i\). De hecho, el vector

\[p(0) = \{p_i(0)= Pr[X(0) = i], \ i \in S\}\] se denomina distribución inicial de la cadena e identifica la distribución de probabilidad del proceso en el instante inicial o punto de partida del proceso.

En formato matricial, cuando el espacio de estados es finito, \(S=\{1,...,N\}\), la distribución marginal transcurridas \(n\) transiciones en el proceso, se obtendrá a partir del vector de probabilidades iniciales \(p(0) =(p_1(0),p_2(0),\ldots,p_N(0))\) y la matriz de transición \(p=(p_{ij})_{i,j =1,...,N}\),

\[\begin{equation} p(n)=p(0) %*% p \end{equation}\]

De forma habitual se suelen expresar las probabilidades de transición de un paso para \(N\) estados en una \(CMTD\) mediante la denominada matriz de transición de un paso \(P\), que es una matriz estocástica con todos sus elementos constituidos por probabilidades, dada por:

\[P = \begin{pmatrix} p_{11} & p_{12} & ... & p_{1N}\\ p_{21} & p_{22} & ... & p_{2N}\\ ... & ... & ... & ...\\ p_{N1} & p_{N2} & ... & p_{NN} \end{pmatrix}\]

La información sobre las probabilidades de transición también puede representarse de forma gráfica construyendo un diagrama de transición del \(CMTD\). Un diagrama de transición es un grafo dirigido con \(N\) nodos, un nodo por cada estado del \(CMTD\). Hay un arco dirigido que va del nodo \(i\) al nodo \(j\) en el grafo si la transición del estado \(i\) al estado \(j\) es viable, esto es, \(p_{ij} \neq 0\). Los diagramas de transición se pueden utilizar como herramienta para visualizar la dinámica de la \(CMTD\).

De forma similar podemos definir la matriz de transición de n pasos con la matriz estocástica \(P(n)\):

\[P(n) = \begin{pmatrix} p_{11}(n) & p_{12}(n) & ... & p_{1N}(n)\\ p_{21}(n) & p_{22}(n) & ... & p_{2N}(n)\\ ... & ... & ... & ...\\ p_{N1}(n) & p_{N2}(n) & ... & p_{NN}(n) \end{pmatrix}\]

con \[\begin{eqnarray*} 0 \leq p_{ij}(n) &\leq& 1 \\ \sum_{j \in S} p_{ij}(n) &=& 1. \end{eqnarray*}\]

De forma genérica denotamos por \(p(n)\) a la distribución del proceso en la n-ésima transición:

\[p(n) = \{p_i(n)=Pr[X(n)=i], \ i \in S\}\]

Cualquier \(CMTD\) homogénea verifica la denominada Ecuación de Chapman-Kolmogorov que permite calcular la probabilidad de transición de un estado \(i\) a un estado \(j\) en \(n\) pasos a través de todas las probabilidades de transición de \(s\) y \(n-s\) pasos, para cualquier \(s<n\) y cualquier \(i\) y \(j\) en \(S\):

\[\begin{equation} p_{ij}(n) = \sum_{k \in S} p_{ik}(s) p_{kj}(n-s), \tag{2.4} \end{equation}\]

Definición 2.4 Haciendo uso de la ecuación (2.4) se puede demostrar que la matriz de transición de \(n\) pasos \(P(n)\) se puede obtener como la potencia \(n\) de la matriz de transición de un paso \(P\), esto es,

\[\begin{equation} P(n) = P^n, \tag{2.5} \end{equation}\]

de modo que conociendo la distribución inicial del proceso \(p(0)\) y la matriz de transición de un paso \(P\), tenemos perfectamente identificada la distribución del proceso en cualquier momento:

\[\begin{equation} p(n) = p(0)P^n. \tag{2.6} \end{equation}\]

Para calcular la matriz de transición de \(n\) pasos en R habrá que utilizar el producto matricial para obtener estas matrices. Definimos entonces una función que nos permitirá calcularla a partir de la matriz de transición de un paso.

# Matriz de probs. transición de n pasos
ptran.n=function(ptran,n){
  # ptran es la matriz de transición de 1 paso
  # n son los pasos a dar
  i=1
  p=ptran
  while(i<n){
    p=p%*%ptran
    i=i+1
  }
return(p)  
}

2.2 Librería markovchain

Para trabajar con procesos \(CMTD\) con R es útil la librería markovchain.³⁰ Trabajamos a continuación sobre un problema sencillo, para crear la matriz y el diagrama de transición de la cadena de Markov.

Ejemplo 2.1 Tenemos una \(CMTD\) \(\{X(t), t \in \mathbb{N}\}\) con espacio de estados \(S = \{a, b, c\}\) y distribución inicial de la cadena dada por \(p_a(0)=0.4, p_b(0)=0.2\) y \(p_c(0)=0.4\). La matriz de transición de un paso viene dada por:

\[P = \begin{pmatrix} 0.20 & 0.30 & 0.50\\ 0.10 & 0.00 & 0.90\\ 0.55 & 0.00 & 0.45 \end{pmatrix}\]

Planteamos resolver las cuestiones siguientes:

(1). Queremos representar el proceso a través de un grafo.

Para representar el proceso con markovchain, hemos de crear un vector con los estados y la matriz de transición con las probabilidades de transición. Definimos entonces el proceso con la función genérica new() para generar un objeto del tipo markovchain:

\[new("markovchain",states,byrow=TRUE,transitionMatrix)\]

introduciendo el vector de estados en states, la matriz de transición en transitionMatrix, y especificando si dicha matriz se ha de leer por filas.

A continuación lo pintamos con la función plot().

Procedemos con el ejemplo que nos atañe. El grafo en la Figura 2.1 muestra los tres estados como nodos y las probabilidades de transición para pasar de un estado a otro en un único paso.

require(markovchain)
# Definimos estados
estados <- c("a", "b", "c")
# Creamos la matriz de transición 
pmat <- matrix(data = c(0.20, 0.30, 0.50, 0.10, 0.00, 0.90,0.55, 0.00, 0.45), 
               byrow = TRUE, nrow = 3, 
               dimnames = list(estados, estados))
# Creamos la CMTD
proceso <- new("markovchain", states = estados, 
               byrow = TRUE, transitionMatrix = pmat)
# Verificamos los datos introducidos
proceso

## Unnamed Markov chain 
##  A  3 - dimensional discrete Markov Chain defined by the following states: 
##  a, b, c 
##  The transition matrix  (by rows)  is defined as follows: 
##      a   b    c
## a 0.20 0.3 0.50
## b 0.10 0.0 0.90
## c 0.55 0.0 0.45

# y obtenemos el diagrama del proceso
plot(proceso)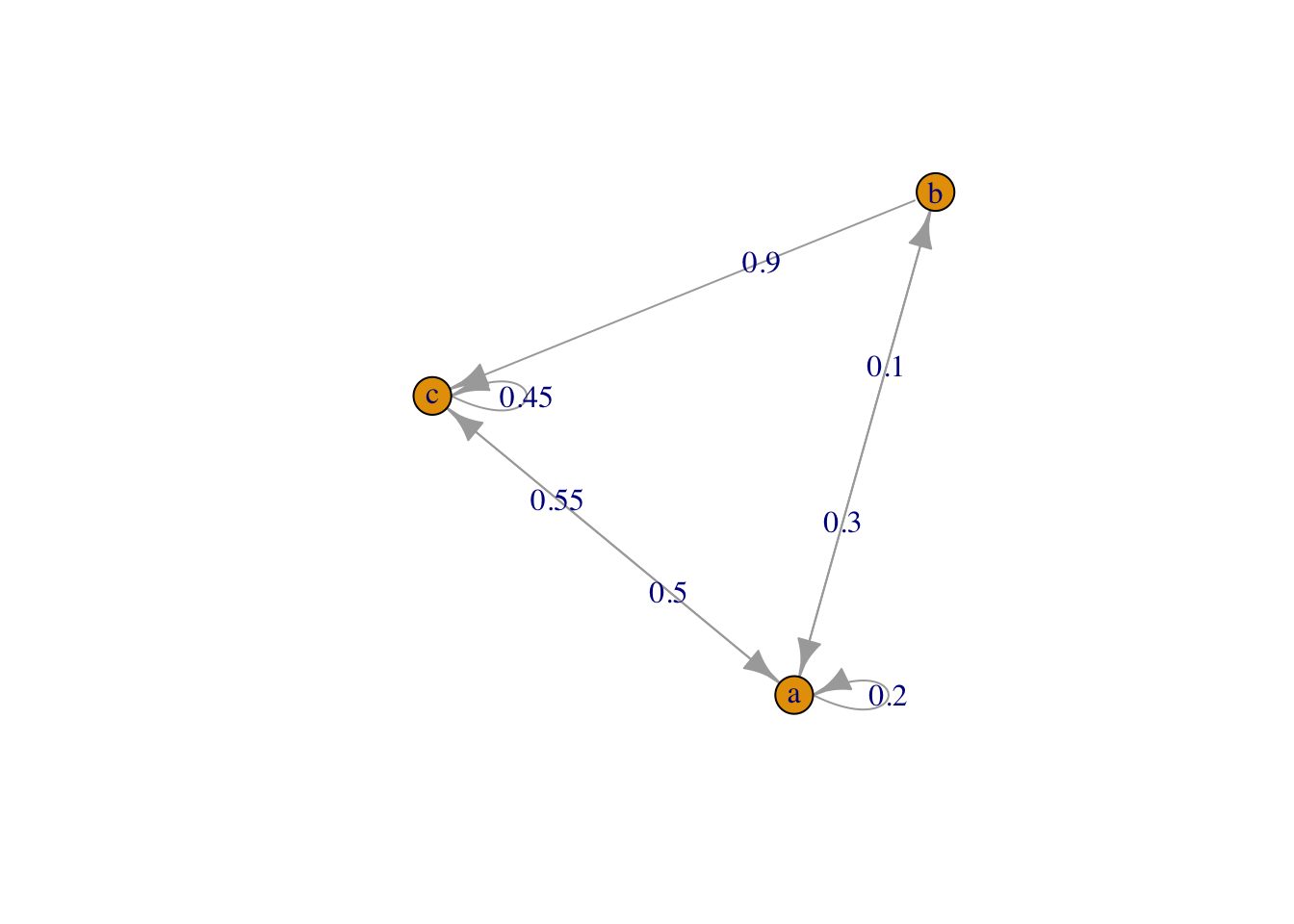

Figura 2.1: Grafo del proceso.

(2). Si la \(CMTD\) está en el estado \(c\) en el momento 17, ¿cuál es la probabilidad de que esté en el estado \(a\) en el momento 18?

• RESPUESTA: Nos preguntan por la probabilidad de transición para pasar, en un solo paso, del estado \(c\) (3) al estado \(a\) (1), por lo que viene dada por la componente \(p_{31}\) de la matriz de transición, es decir, 0.55.

Para resolver el cálculo con el ordenador basta utilizar la función transitionProbability(), con los argumentos: object (la cadena de markov), t0 (el estado en el instante inicial), t1 (el estado en el instante final).

Así la pregunta (2) se responde con:

transitionProbability(object = proceso, t0 = "c", t1 = "a")

## [1] 0.55

(3). Si la \(CMTD\) está en el estado \(c\) en un momento dado, ¿cuál es la probabilidad de que esté en el estado \(a\) transcurridos tres unidades de tiempo? ¿y después de 10?

• RESPUESTA: Para resolver esta cuestión definimos el estado inicial y lo multiplicamos por la matriz de transición que corresponda, que en este caso, aplicando la Ecuación (2.5), será \(P^n\), para \(n=3\) y \(n=10\). Obtendremos así la distribución de probabilidad en \(n\) transiciones, con la probabilidad de llegar a cada uno de los eventos posibles, \(\{a,b,c\}\) en \(n\), partiendo de un estado inicial dado.

# Estado inicial en c
sini <- c(0, 0, 1)
# matriz de transición de 3 pasos
mt3 <- ptran.n(pmat,3);mt3

##          a       b        c
## a 0.402250 0.10350 0.494250
## b 0.356250 0.15450 0.489250
## c 0.350625 0.10725 0.542125

# o bien extrayendo la matriz de transición del proceso
ptran.n(proceso[1:3,1:3],3)

##          a       b        c
## a 0.402250 0.10350 0.494250
## b 0.356250 0.15450 0.489250
## c 0.350625 0.10725 0.542125

# Situación del proceso dentro de 3 instantes
sini%*%mt3

##             a       b        c
## [1,] 0.350625 0.10725 0.542125

# matriz de transición de 10 pasos
mt10 <-ptran.n(pmat,10)
# Situación del proceso dentro de 10 instantes
sini%*%mt10

##              a         b         c
## [1,] 0.3703899 0.1110948 0.5185153

(4). ¿Cuál es la distribución de probabilidad del proceso transcurridos \(10\) instantes de tiempo desde el momento inicial del proceso, sea cual sea su estado?

• RESPUESTA: Si conocemos la distribución de probabilidad en el estado inicial, \(p(0)\), podemos obtener la distribución de probabilidad en \(n\) transiciones con la Ecuación :

### Distribución de probabilidad del proceso dentro de 10 instantes
# Distribución de  probabilidad inicial
dini <- c(0.4, 0.2, 0.4)
# matriz de transición de 10 pasos
mt10 <- ptran.n(pmat,10)
# distribución de probabilidad marginal en 10 pasos: inicial x condicional
dini%*%mt10

##             a         b         c
## [1,] 0.370364 0.1111134 0.5185226

En base a la distribución del proceso tras \(n=10\) pasos, apreciamos que lo más probable es que el sistema se ecuentre en el estado “c” (prob=0.52), y lo menos probable es que se encuentre en el estado “b” (prob=0.11).

(5). Corroborar los resultados analíticos obtenidos en (4) con simulaciones.

• RESPUESTA: Para ver el comportamiento de un proceso después de que transcurran \(n\) pasos habrá que simularlo durante \(n\) instantes de tiempo. Puesto que buscamos una estimación de lo que va a ocurrir en ese momento, simularemos \(nsim=100\) veces el proceso hasta el instante \(n=10\), nos quedaremos con el estado en que se encuentra el proceso en ese instante \(n\) y evaluaremos las probabilidades obtenidas para los tres estados \(\{a,b,c\}\). Los resultados serán más próximos a la solución analítica, cuanto mayor sea el número de simulaciones (prueba a modificar \(nsim\)).

Para simular una CMTD hasta una transición \(n\) con la librería markovchain basta utilizar la función rmarkovchain(n, proceso), donde proceso ha sido definido previamente con la función new().

### Simulación del proceso para n=10 instantes 
res=vector()
nsim=100
n=10
for(i in 1:nsim){
  res[i]=rmarkovchain(n, proceso)[n]}
prop.table(table(res))

## res
##    a    b    c 
## 0.31 0.12 0.57

2.3 Aplicaciones

Las aplicaciones de las CMTD son muy numerosas. A continuación presentamos una colección de ejemplos basados en aplicaciones prácticas de estos procesos, con algunos de los cuales trabajaremos a lo largo de la unidad.

2.3.1 Colas de espera

Supongamos una consulta médica en un centro de salud, en el que los pacientes que llegan se colocan en una única cola de espera, son atendidos consecutivamente y sólo se atiende a un paciente en cada periodo de 5 minutos. Consideramos las variables aleatorias:

• \(Y_n:\) Número de clientes que acuden a la consulta durante el n-ésimo periodo de servicio, con posibles valores \(\{0, 1, 2,...\}\) donde

\[Pr(Y_n = k) = a_k, \quad k=0, 1, 2,...; \quad 0 \leq a_k \leq 1; \quad \sum_{k=0}^{\infty} a_k =1\]

• \(X_n:\) Número de pacientes que hay esperando en la cola en el momento que empieza el n-ésimo periodo de servicio, con posibles valores \(\{0, 1, 2,...\}\), que conforman un proceso estocástico discreto con:

\[\begin{equation*} X_{n+1} = \begin{cases} Y_n & \text{ si } X_n = 0\\ X_n - 1 + Y_n & \text{ si } X_n \neq 0 \end{cases} \end{equation*}\]

de forma que cada \(X_n\) sólo dependerá de lo que haya ocurrido en el periodo inmediatamente anterior, luego \(\{X_n, n \in \mathbb{N}\}\) es una \(CMTD\), con probabilidades de transición dadas por:

\[\begin{eqnarray*} p_{0j} &=& Pr[X_{n+1} = j | X_{n} = 0] = Pr[Y_n = j] = a_j \\ p_{ij} &=&Pr[X_{n+1} = j | X_{n} = i] = Pr[i - 1 + Y_n = j] = a_{j-i+1}; \quad i\neq 0; \ j \geq i-1 \\ p_{ij} &=& 0; \quad j+1<i\neq0. \end{eqnarray*}\]

La matriz de transición viene dada por:

\[P = \begin{pmatrix} a_0 & a_1 & a_2 & a_3 &...& a_j & ...\\ a_0 & a_1 & a_2 & a_3 &...& a_j & ...\\ 0 & a_0 & a_1 & a_2 &...& a_{j-1} & ...\\ 0 & 0 & a_0 & a_1 &...& a_{j-2} & ...\\ ... & ... & ... & ... &...& ... & ... \end{pmatrix}\]

2.3.2 Fiabilidad de máquinas

La empresa Depend-On-Us fabrica una máquina que está encendida o apagada (“On”/“Off”). Si está “On” al principio de un día, entonces está “On” al principio del día siguiente con una probabilidad de 0.98 (independientemente del historial de la máquina), o falla con una probabilidad de 0.02. Una vez que la máquina falla, la empresa envía a una persona para que la repare. Si la máquina está averiada al principio de un día, está “Off” al principio del día siguiente con una probabilidad de 0.03 (independientemente del historial de la máquina), o la reparación se completa y la máquina está “On” con probabilidad de 0.97. Una máquina reparada está como nueva.

Podemos modelar este sistema mediante una \(CMTD\) si consideramos la variable aleatoria \(X_n\) que refleja el estado de la máquina en el día \(n\) definida como:

\[\begin{equation*} X_{n} = \begin{cases} 0 & \text{ Off}\\ 1 & \text{ On} \end{cases} \end{equation*}\]

de forma que la matriz de transicción viene dada por:

\[P = \begin{pmatrix} 0.03 & 0.97\\ 0.02 & 0.98 \end{pmatrix}\]

Supongamos ahora que la empresa mantiene dos máquinas de este tipo que son idénticas, se comportan de forma independiente y cada una tiene su propio reparador.

Sea \(Y_n\) el número de máquinas en estado “On” al principio del día \(n\), que constituye una CMTD cuyo espacio de estados es \(\{0, 1, 2\}\), puesto que la situación de las máquinas un día cualquiera sólo depende de cómo estaban el día anterior (cumplen la Ecuación (2.1).

Calculemos la probabilidad de transición para un caso concreto: \(Y_n = i = 1\) e \(Y_{n+1} = j = 0\), que identifica una situación en la que una máquina está en funcionamiento y otra en paro el día \(n\), pero al día siguiente ambas están paradas. Así, la máquina que está “Off” el día \(n\) debe permanecer “Off” al día siguiente, y la máquina que está “On” debe cambiar a “Off” el día siguiente. Como las máquinas son independientes, la probabilidad de cambio de estado es:

\[p_{10}=Pr[Y_{n+1} = 0 | Y_n = 1] = 0.03 * 0.02 = 0.0006\] Procediendo de la misma forma obtenemos la matriz completa de transición de un paso del proceso como:

\[P = \begin{pmatrix} 0.0009 & 0.0582 & 0.9409\\ 0.0006 & 0.0488 & 0.9506\\ 0.0004 & 0.0392 & 0.9604 \end{pmatrix}\]

Representamos a continuación este sistema en forma de grafo en la Figura 2.2. Para ello acudimos a la librería markovchain.

# Definimos estados
estados <- c("0", "1", "2")
# Matriz de transición 
pmat <- matrix(data = c(0.0009, 0.0582, 0.9409, 
                        0.0006, 0.0488, 0.9506, 
                        0.0004, 0.0392, 0.9604), 
               byrow = TRUE, nrow = 3, 
               dimnames = list(estados, estados))
# CMTD
fiabilidad <- new("markovchain", states = estados, 
                 byrow = TRUE, transitionMatrix = pmat, 
                 name = "Fiabilidad")
# Verificamos los datos introducidos
fiabilidad

## Fiabilidad 
##  A  3 - dimensional discrete Markov Chain defined by the following states: 
##  0, 1, 2 
##  The transition matrix  (by rows)  is defined as follows: 
##       0      1      2
## 0 9e-04 0.0582 0.9409
## 1 6e-04 0.0488 0.9506
## 2 4e-04 0.0392 0.9604

# Diagrama
plot(fiabilidad, vertex.color="steelblue", 
     vertex.label.font = 2, 
     edge.label.size = 0.1,
     edge.arrow.size=0.5, 
     vertex.shape = "rectangle", 
     vertex.size = 20)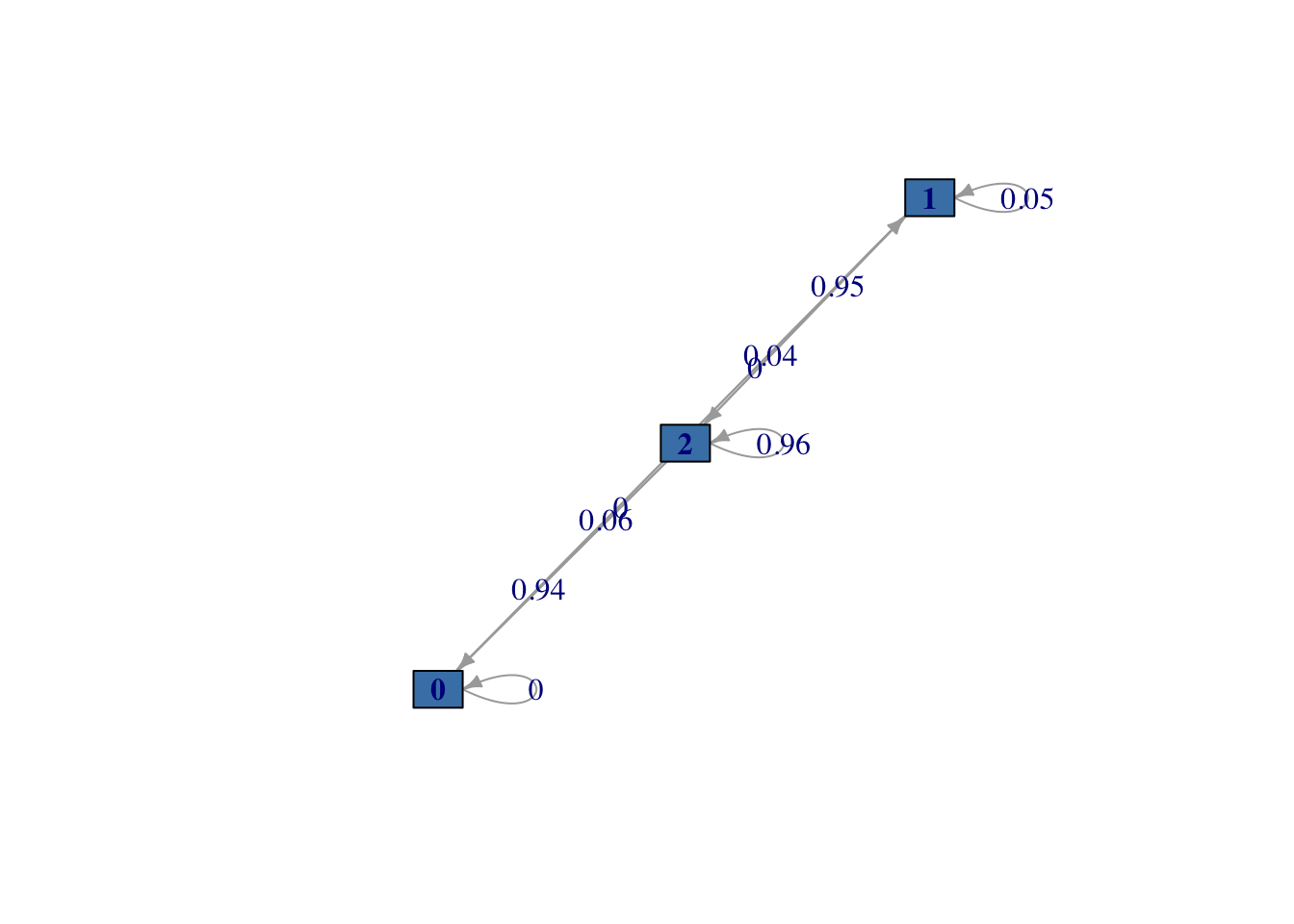

Figura 2.2: Diagrama del sistema de fiabilidad

2.3.3 Meteorología

El tiempo en la ciudad de Heavenly se clasifica como soleado, nublado o lluvioso. Supongamos que el tiempo de mañana depende sólo del tiempo de hoy de la siguiente manera: si hoy hace sol, mañana estará nublado con una probabilidad de 0.3 y lluvioso con probabilidad 0.2; si hoy está nublado, mañana estará soleado con probabilidad 0.5 y lluvioso con probabilidad 0.3; y finalmente, si hoy está lluvioso, mañana estará soleado con probabilidad 0.4 y nublado con probabilidad 0.5.

Consideramos la variable aleatoria \(X_n\) que registra las condiciones meteorológicas del día \(n\) como:

\[\begin{equation*} X_{n} = \begin{cases} 1 & \text{ soleado}\\ 2 & \text{ nublado}\\ 3 & \text{ lluvioso} \end{cases} \end{equation*}\]

de forma que el proceso \(\{X_n, n \in \mathbb{N}\}\) con espacio de estados \(S = \{1, 2, 3\}\) se puede considerar como una \(CMTD\), cuya matriz de transición se puede obtener de forma muy rápida como:

\[P = \begin{pmatrix} 0.50 & 0.30 & 0.20\\ 0.50 & 0.20 & 0.30\\ 0.40 & 0.50 & 0.10 \end{pmatrix}\]

Representamos a continuación este sistema en forma de grafo en la Figura 2.3.

# Definimos estados
estados <- c("Soleado", "Nublado", "LLuvioso")
# Matriz de transición 
pmat <- matrix(data = c(0.50, 0.30, 0.20, 
                        0.50, 0.20, 0.30, 
                        0.40, 0.50, 0.10), 
               byrow = TRUE, nrow = 3, 
               dimnames = list(estados, estados))
# CMTD
meteo <- new("markovchain", states = estados, 
                 byrow = TRUE, transitionMatrix = pmat, 
             name = "Meteorología")
# Verificamos los datos introducidos
meteo

## Meteorología 
##  A  3 - dimensional discrete Markov Chain defined by the following states: 
##  Soleado, Nublado, LLuvioso 
##  The transition matrix  (by rows)  is defined as follows: 
##          Soleado Nublado LLuvioso
## Soleado      0.5     0.3      0.2
## Nublado      0.5     0.2      0.3
## LLuvioso     0.4     0.5      0.1

# Diagrama
plot(meteo, vertex.color="steelblue", 
     vertex.label.font = 2, 
     edge.label.size = 0.1,
     edge.arrow.size=0.5, 
     vertex.shape = "rectangle", 
     vertex.size = 60)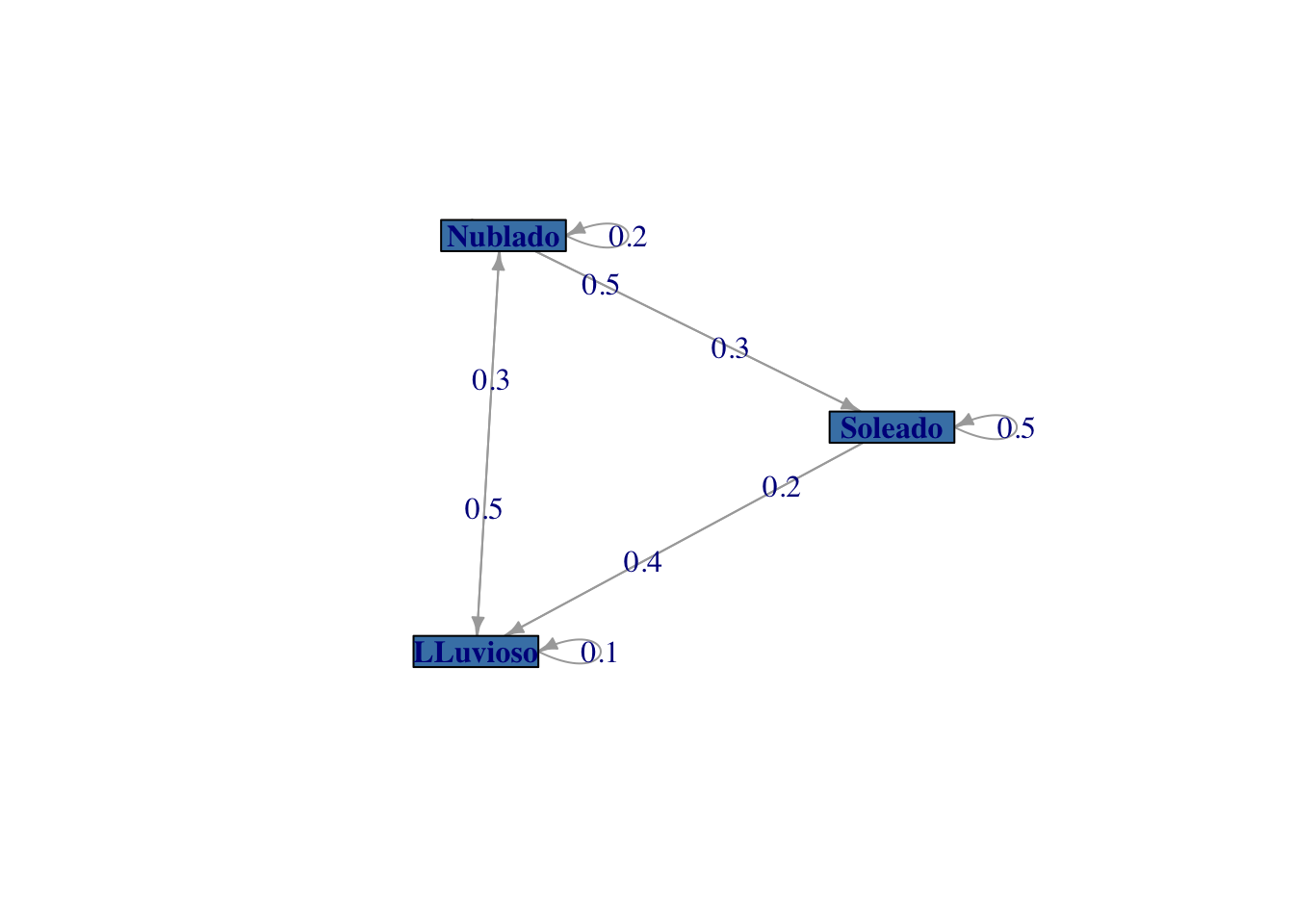

Figura 2.3: Diagrama del sistema de metereología

2.3.4 Problema de inventario

Computers-R-Us almacena una amplia variedad de PCs para la venta al por menor. La tienda abre de lunes a viernes de 8:00 a.m. a 5:00 p.m., y utiliza la siguiente política operativa para controlar el inventario al inicio de semana, en función del número de PCs que quedan en stock el viernes de la semana anterior a las 5:00 p.m:

• Si el stock al finalizar una semana es inferior a dos, se piden suficientes ordenadores para disponer de un stock total de cinco al inicio la semana siguiente.

• Si el stock al final de la semana es de dos o más, no se realiza ningún pedido.

La demanda de ordenadores durante la semana es una variable aleatoria de Poisson con media 3. Cualquier demanda que no pueda ser satisfecha inmediatamente se pierde.

Se consideran las variables aleatorias:

• \(X_n:\) número de PCs en stock a las 8:00 a.m del lunes de la semana \(n\).
• \(D_n:\) número de PCs demandados durante la semana \(n\).

De esta forma el número de Pcs que hay en la tienda al inicio de la semana \(n+1\) viene dado por los que habían en stock al inicio de la semana anterior menos los que se han vendido, siempre que dicho balance sea al menos de 2 unidades, y será de 5 en otro caso:

\[\begin{equation*} X_{n+1} = \begin{cases} X_n - D_n & \text{ si } X_n - D_n \geq 2\\ 5 & \text{ si } X_n - D_n < 2 \end{cases} \end{equation*}\]

Necesariamente entonces, \(X_{n+1} \geq X_n\) dado que \(D_n \geq 0\).

Se trata de una CMTD con espacio de estados \(\{2, 3, 4, 5\}\), puesto que el estado del sistema en la semana \(n+1\) sólo depende de su estado en la semana anterior \(n\). Calculemos las probabilidades de transición.

• Para \(j= 2, 3, 4\)

\[\begin{array}{ll} Pr[X_{n+1} = j | X_n = i] & = Pr[X_n - D_n = j | X_n = i]\\ & = Pr[D_n=X_n-j | X_n = i]\\ & = Pr[D_n = i - j] \\ &=\begin{cases} Pr[D_n = i - j] \quad \text{ si } i\geq j \\ 0 \qquad \qquad \qquad \quad \text{ si } i< j \end{cases} \end{array}\]

• Para \(j=5\) e \(5>i\geq 2\)

\[\begin{array}{ll} Pr[X_{n+1} = 5 | X_n = i] & = Pr[X_n - D_n \leq 1 | X_n = i]\\ &=Pr[D_n \geq X_n-1|X_n=i] \\ & = Pr(D_n \geq i - 1). \end{array}\]

• Para \(j=5\) e \(i=5\), podría ocurrir que durante la semana anterior no se hubiera vendido nada \(D_n=0\) o se hubieran vendido al menos cuatro ordenadores, \(D_n \geq 4\) (para dejar un stock inferior a 2),

\[\begin{array}{ll} Pr[X_{n+1} = 5 | X_n = 5] & = Pr[X_n - D_n =5 | X_n = 5]\\ &=Pr[D_n =0] + Pr(D_n \geq 4). \end{array}\]

Usando el hecho de que la variable \(D_n \sim Po(3)\) podemos obtener la tabla de probabilidades siguientes:

\(k\)	0	1	2	3	4
\(Pr[D_n = k]\)	0.0498	0.1494	0.2240	0.2240	0.1680
\(Pr[D_n \geq k]\)	1.0000	0.9502	0.8008	0.5768	0.3528

Usando los datos de esta tabla calculamos fácilmente la matriz de transición asociada a la \(CMTD\) como:

\[P = \begin{pmatrix} 0.0498 & 0 & 0 & 0.9502\\ 0.1494 & 0.0498 & 0 & 0.8008\\ 0.2240 & 0.1494 & 0.0498 & 0.5768\\ 0.2240 & 0.2240 & 0.1494 & 0.4026 \end{pmatrix}\]

Representamos a continuación este sistema en forma de grafo en la Figura 2.4.

# Definimos estados
estados <- c("2 PCs", "3 PCs", "4 PCs", "5 PCs")
# Matriz de transición 
pmat <- matrix(data = c(0.0498, 0, 0, 0.9502, 
                        0.1494, 0.0498, 0, 0.8008,  
                        0.2240, 0.1494, 0.0498, 0.5768,
                        0.2240, 0.2240, 0.1494, 0.4026), 
               byrow = TRUE, nrow = 4, 
               dimnames = list(estados, estados))
# CMTD
inventario <- new("markovchain", states = estados, 
                 byrow = TRUE, transitionMatrix = pmat, 
                 name = "inventario")
# Verificamos los datos introducidos
inventario

## inventario 
##  A  4 - dimensional discrete Markov Chain defined by the following states: 
##  2 PCs, 3 PCs, 4 PCs, 5 PCs 
##  The transition matrix  (by rows)  is defined as follows: 
##        2 PCs  3 PCs  4 PCs  5 PCs
## 2 PCs 0.0498 0.0000 0.0000 0.9502
## 3 PCs 0.1494 0.0498 0.0000 0.8008
## 4 PCs 0.2240 0.1494 0.0498 0.5768
## 5 PCs 0.2240 0.2240 0.1494 0.4026

# Diagrama
plot(inventario, vertex.color="steelblue", 
     vertex.label.font = 2, 
     edge.label.size = 0.1,
     edge.arrow.size=0.5, 
     vertex.shape = "rectangle", 
     vertex.size = 40)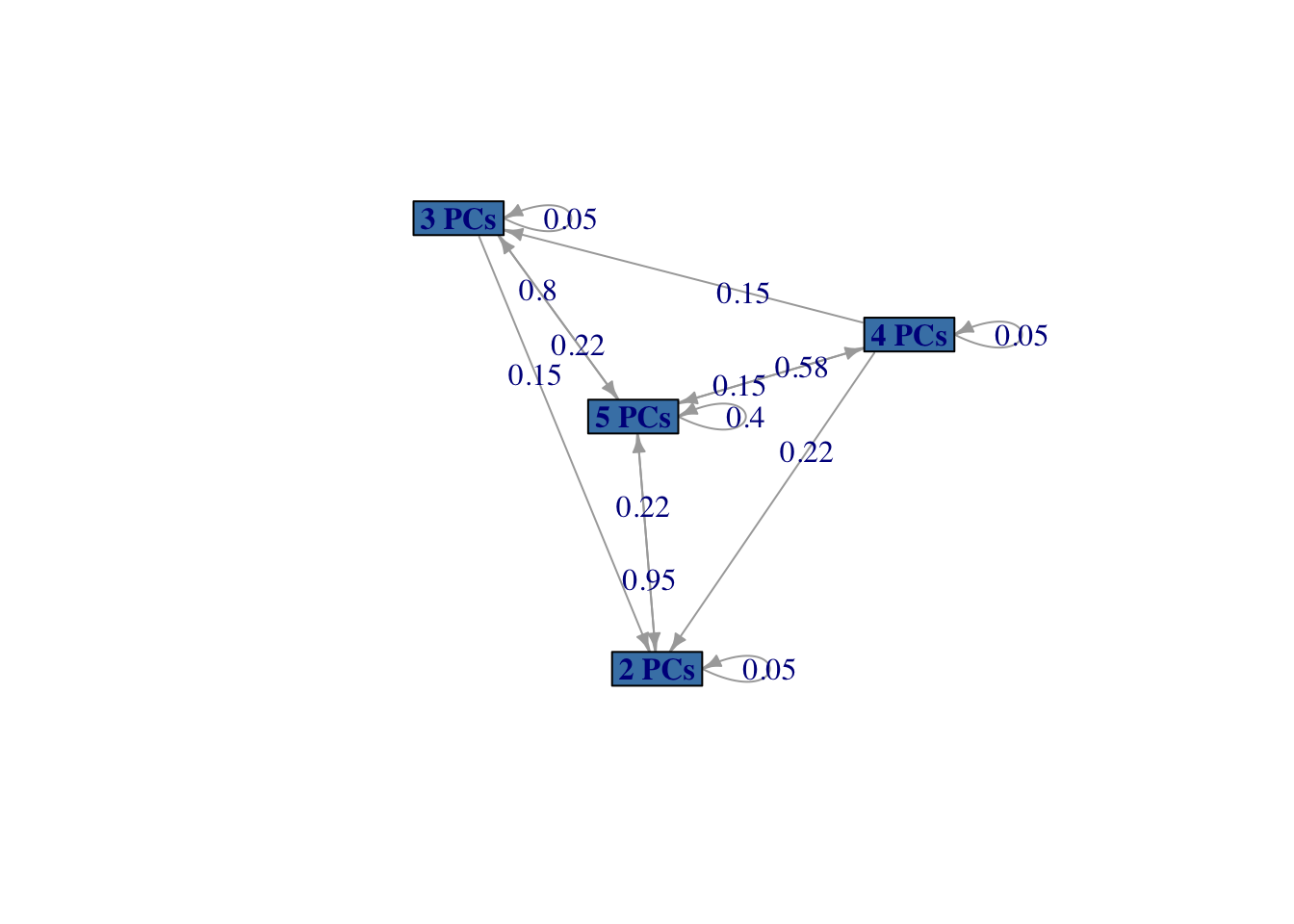

Figura 2.4: Diagrama del sistema de inventario

2.3.5 Planificación de mano de obra

Paper Pushers, Inc. es una empresa de seguros que emplea a 100 trabajadores organizados en cuatro grados, etiquetados como \(1\), \(2\), \(3\) y \(4\). Por razones de simplicidad, supondremos que los trabajadores pueden ser promovidos de un grado a otro, o dejar la empresa, sólo al principio de la semana. Un trabajador en el grado 1 al principio de la semana asciende al grado 2 con probabilidad 0.03, deja la empresa con una probabilidad de 0.02, o continúa en el mismo grado al principio de la semana siguiente. Un trabajador que se encuentra en el grado 2 al principio de la semana asciende al grado 3 con probabilidad 0.01, abandona la empresa con probabilidad 0.008 o continúa en el mismo grado al principio de la semana siguiente. Un trabajador de grado 3 al principio de la semana asciende al grado 4 con una probabilidad de 0.005, abandona la empresa con una probabilidad de 0.02, o continúa en el mismo grado al principio de la semana siguiente. Un trabajador que se encuentra en el grado 4 al principio de la semana deja la empresa con una probabilidad de 0.01 o continúa en el mismo grado al principio de la semana siguiente. Si un trabajador abandona la empresa, es sustituido instantáneamente por otro de grado 1. El movimiento de los trabajadores dentro de la empresa puede modelizarse utilizando una \(CMTD\).

Supondremos que todos los ascensos de los trabajadores se deciden de manera independiente. Esto simplifica considerablemente nuestro modelo. En lugar de hacer un seguimiento de los 100 trabajadores, tenemos en cuenta a un único trabajador, digamos el trabajador \(k\), donde \(k = 1, 2,...,100\). Pensamos en \(k\) como un ID de trabajador, y cuando este trabajador deja la empresa, se le asigna al nuevo sustituto. Sea \(X_n^k\) el grado en el que se encuentra el trabajador \(k\) al principio de la n-ésima semana. Ahora, si suponemos que los ascensos de los trabajadores se determinan independientemente del historial del trabajador (es decir, que el tiempo transcurrido en un grado determinado no afecta a las posibilidades de promoción), vemos que para \(k = 1, 2,...,100\) el conjunto \(\{X_n^k, n \in \mathbb{N}\}\) es una \(CMTD\) con espacio de estados \(S =\{1, 2, 3, 4\}\).

Para obtener la matriz de transiciones procedemos con un ejemplo. Supongamos que \(X_n^k = 3\) entonces:

• Si es promocionado (\(X_{n+1}^k = 4\)), tenemos que \(Pr[X_{n+1}^k = 4 | X_n^k = 3] = 0.005.\)
• Si deja la empresa, es reemplazado por un nuevo empleado de grado 1 (\(X_{n+1}^k = 1\)) de forma que \(Pr[X_{n+1}^k = 1 | X_n^k = 3] = 0.02.\)
• Si se mantiene en el mismo puesto, tenemos que \(Pr[X_{n+1}^k = 3 | X_n^k = 3] = 0.975.\)

Procediendo de forma similar en el resto de situaciones tenemos la matriz de transición para cualquiera de los trabajadores como:

\[P = \begin{pmatrix} 0.970 & 0.030 & 0 & 0\\ 0.008 & 0.982 & 0.010 & 0\\ 0.020 & 0 & 0.975 & 0.005\\ 0.010 & 0 & 0 & 0.990 \end{pmatrix}\]

Representamos a continuación este sistema en forma de grafo en la Figura 2.5.

# Definimos estados
estados <- c("1", "2", "3", "4")
# Matriz de transición 
pmat <- matrix(data = c(0.9700, 0.0300, 0, 0, 
                        0.0080, 0.9820, 0.0100, 0,   
                        0.0200, 0, 0.9750, 0.0050,
                        0.0100, 0, 0, 0.9900), 
               byrow = TRUE, nrow = 4, 
               dimnames = list(estados, estados))
# CMTD
planificacion <- new("markovchain", states = estados, 
                 byrow = TRUE, transitionMatrix = pmat, 
                 name = "planificacion")
# Verificamos los datos introducidos
planificacion

## planificacion 
##  A  4 - dimensional discrete Markov Chain defined by the following states: 
##  1, 2, 3, 4 
##  The transition matrix  (by rows)  is defined as follows: 
##       1     2     3     4
## 1 0.970 0.030 0.000 0.000
## 2 0.008 0.982 0.010 0.000
## 3 0.020 0.000 0.975 0.005
## 4 0.010 0.000 0.000 0.990

# Diagrama
plot(planificacion, vertex.color="steelblue", 
     vertex.label.font = 2, 
     vertex.label.color = "white",
     edge.label.size = 0.2,
     edge.arrow.size=0.5, 
     vertex.shape = "rectangle",
     vertex.size = 20)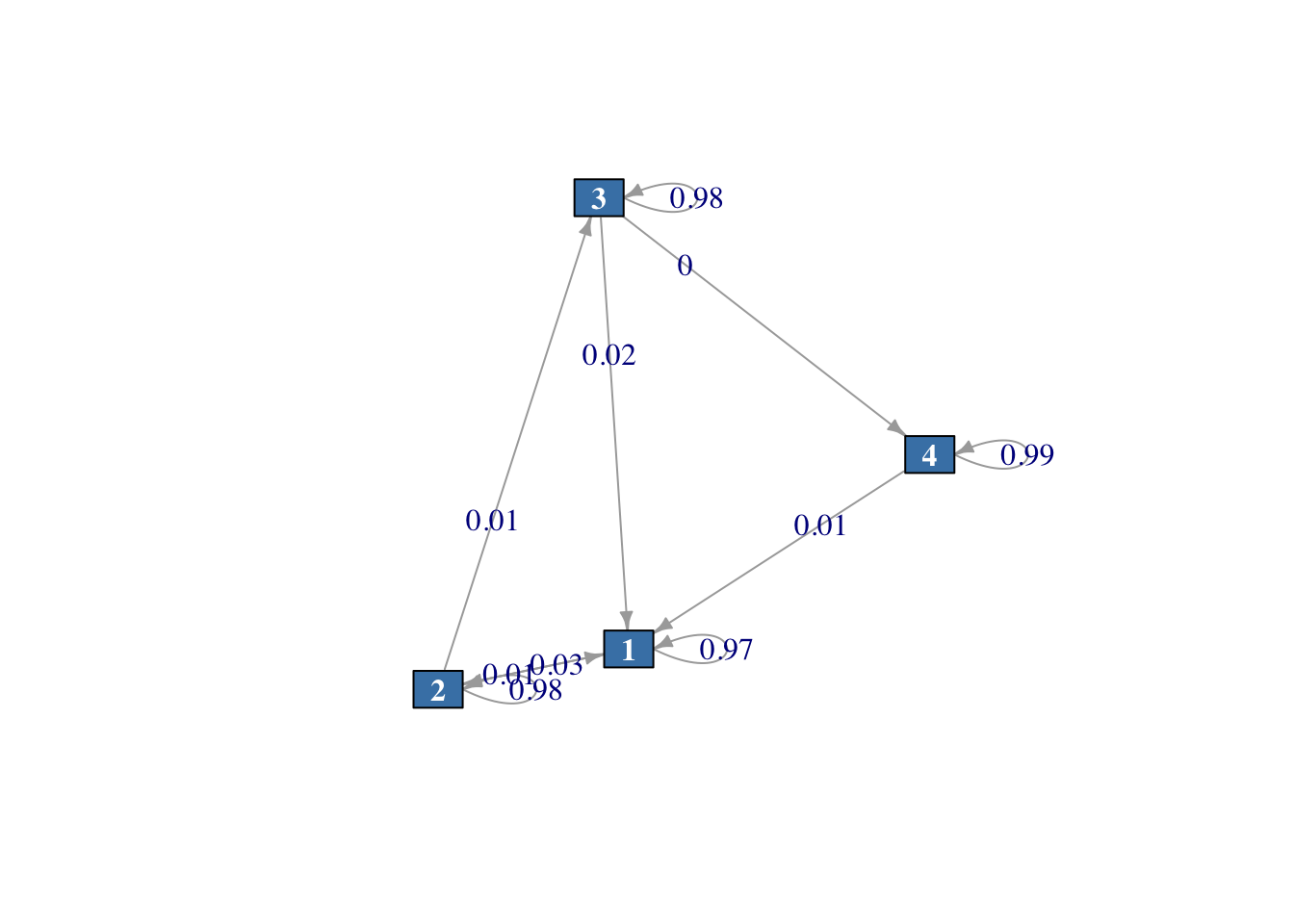

Figura 2.5: Diagrama del sistema de planificación

2.3.6 Mercado de valores

Las acciones ordinarias de la empresa Gadgets-R-Us se cotizan en el mercado de valores. El director financiero de Gadgets-R-Us compra y vende las acciones de su propia empresa para que el precio nunca baje de 2 dólares y nunca supere los 10 dólares (cuando esto ocurre, vende). Para simplificar, suponemos que \(X_n\), es el precio de cada acción al final del día \(n\), y sólo toma valores enteros; es decir, el espacio de estados del proceso \(\{X_n, n \in \mathbb{N}\}\) es \(S = 2, 3,...,10\). Si denominamos \(I_{n+1}\) al movimiento potencial del precio de las acciones en el día \(n+1\) en ausencia de cualquier intervención del director financiero, entonces tenemos que:

\[\begin{equation*} X_{n+1} = \begin{cases} 2 & \text{ si } X_n + I_{n+1} \leq 2\\ X_n + I_{n+1} & \text{ si } 2 < X_n + I_{n+1} < 10\\ 10 & \text{ si } X_n + I_{n+1} \geq 10 \end{cases} \end{equation*}\]

Un análisis continuado de los datos del pasado sugiere que los movimientos potenciales \(\{I_n, n \geq 1\}\) son una secuencia de variables iid con función de masa de probabilidad dada por:

\[Pr(I_n = k) = 0.2, \quad k = -2, -1, 0, 1, 2.\]

Esto implica que \(\{X_n, n \in \mathbb{N}\}\) es una \(CMTD\) con espacio de estados \(S = \{2, 3,...,10\}\), donde las probabilidades de transición se pueden obtener de forma sencilla. A modo de ejemplo presentamos los tres casos siguientes:

\[\begin{array}{ll} Pr[X_{n+1} = 2 | X_n = 3] & = Pr[X_n + I_{n+1} \leq 2 | X_n = 3]\\ & = Pr[I_{n+1} \leq -1]= 0.4 \end{array}\]

\[\begin{array}{ll} Pr[X_{n+1} = 6 | X_n = 5] & = Pr[X_n + I_{n+1} = 6 | X_n = 5]\\ & = Pr[I_{n+1} = 1] = 0.2 \end{array}\]

\[\begin{array}{ll} Pr[X_{n+1} = 10 | X_n = 10] & = Pr[X_n + I_{n+1} \geq 10 | X_n = 10]\\ & = Pr[I_{n+1} \geq 0] = 0.6 \end{array}\]

de forma que la matriz de transición del sistema viene dada por:

\[P = \begin{pmatrix} 0.6 & 0.2 & 0.2 & 0 & 0 & 0 & 0 & 0 & 0\\ 0.4 & 0.2 & 0.2 & 0.2 & 0 & 0 & 0 & 0 & 0\\ 0.2 & 0.2 & 0.2 & 0.2 & 0.2 & 0 & 0 & 0 & 0\\ 0 & 0.2 & 0.2 & 0.2 & 0.2 & 0.2 & 0 & 0 & 0\\ 0 & 0 & 0.2 & 0.2 & 0.2 & 0.2 & 0.2 & 0 & 0\\ 0 & 0 & 0 & 0.2 & 0.2 & 0.2 & 0.2 & 0.2 & 0\\ 0 & 0 & 0 & 0 & 0.2 & 0.2 & 0.2 & 0.2 & 0.2\\ 0 & 0 & 0 & 0 & 0 & 0.2 & 0.2 & 0.2 & 0.4\\ 0 & 0 & 0 & 0 & 0 & 0 & 0.2 & 0.2 & 0.6 \end{pmatrix}\]

Representamos a continuación este sistema en forma de grafo en la Figura 2.6.

# Definimos estados
estados <- c("2", "3", "4", "5", "6", "7", "8", "9", "10")
# Matriz de transición 
pmat <- matrix(data = c(0.6 , 0.2 , 0.2 , 0 , 0 , 0 , 0 , 0 , 0,
                        0.4 , 0.2 , 0.2 , 0.2 , 0 , 0 , 0 , 0 , 0,
                        0.2 , 0.2 , 0.2 , 0.2 , 0.2 , 0 , 0 , 0 , 0,
                        0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2 , 0 , 0 , 0,
                        0 , 0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2 , 0 , 0,
                        0 , 0 , 0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2 , 0,
                        0 , 0 , 0 , 0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2,
                        0 , 0 , 0 , 0 , 0 , 0.2 , 0.2 , 0.2 , 0.4,
                        0 , 0 , 0 , 0 , 0 , 0 , 0.2 , 0.2 , 0.6), 
               byrow = TRUE, nrow = 9, 
               dimnames = list(estados, estados))
# CMTD
mercado.valores <- new("markovchain", states = estados, 
                 byrow = TRUE, transitionMatrix = pmat, 
                 name = "Mercado de valores")
# Verificamos los datos introducidos
mercado.valores

## Mercado de valores 
##  A  9 - dimensional discrete Markov Chain defined by the following states: 
##  2, 3, 4, 5, 6, 7, 8, 9, 10 
##  The transition matrix  (by rows)  is defined as follows: 
##      2   3   4   5   6   7   8   9  10
## 2  0.6 0.2 0.2 0.0 0.0 0.0 0.0 0.0 0.0
## 3  0.4 0.2 0.2 0.2 0.0 0.0 0.0 0.0 0.0
## 4  0.2 0.2 0.2 0.2 0.2 0.0 0.0 0.0 0.0
## 5  0.0 0.2 0.2 0.2 0.2 0.2 0.0 0.0 0.0
## 6  0.0 0.0 0.2 0.2 0.2 0.2 0.2 0.0 0.0
## 7  0.0 0.0 0.0 0.2 0.2 0.2 0.2 0.2 0.0
## 8  0.0 0.0 0.0 0.0 0.2 0.2 0.2 0.2 0.2
## 9  0.0 0.0 0.0 0.0 0.0 0.2 0.2 0.2 0.4
## 10 0.0 0.0 0.0 0.0 0.0 0.0 0.2 0.2 0.6

# Diagrama
plot(mercado.valores, vertex.color="steelblue", 
     vertex.label.font = 2, 
     vertex.label.color = "white",
     edge.label.size = 0.2,
     edge.arrow.size=0.5, 
     vertex.shape = "rectangle",
     vertex.size = 20)

Figura 2.6: Diagrama del sistema del Mercado de valores

2.3.7 Telecomunicaciones

La empresa Tel-All Switch Corporation fabrica equipos de conmutación para redes de comunicación. Las redes de comunicación mueven los datos de un conmutador a otro a la velocidad del rayo en forma de paquetes, es decir, mediante cadenas de ceros y unos (llamadas bits). Los conmutadores Tel-All manejan paquetes de datos de longitud constante, es decir, el mismo número de bits en cada paquete. A nivel conceptual podemos pensar en el conmutador como un dispositivo de almacenamiento donde los paquetes llegan desde la red de usuarios según un proceso aleatorio, se almacenan en un buffer con capacidad para almacenar \(K\) paquetes y se eliminan del buffer uno a uno según un protocolo preestablecido. Uno de los protocolos utilizados considera el tiempo dividido en intervalos de duración fija llamados “ranuras” (por ejemplo, un microsegundo), y consiste en que: si hay algún paquete en el buffer al principio de un intervalo o ranura, se elimina uno instantáneamente; si no hay ningún paquete al principio de un intervalo, no se elimina ningún paquete durante el intervalo, aunque lleguen más paquetes durante el mismo; por último, si un paquete llega durante una ranura y no hay espacio para él, se descarta. Este proceso se puede modelar como una \(CMTD\).

Sean:

• \(A_n\) el número de paquetes que llegan al conmutador durante la enésima ranura (algunos pueden ser descartados)
• \(X_n\) el número de paquetes en el buffer al final de la enésima ranura.

Ahora, si \(X_n = 0\), entonces no hay paquetes disponibles para la transmisión al principio de la ranura \(n+1\). Por lo tanto, todos los paquetes que llegan durante esa ranura, es decir, \(A_{n+1}\), están en el buffer al final de esa ranura mientras tenga capacidad, esto es, \(A_{n+1} \leq K\); si \(A_{n+1}>K\), entonces la memoria intermedia está llena al final de la ranura \(n+1\), \(X_{n+1}=K\). Por lo tanto, en general \(X_{n+1} = min(A_{n+1}, K)\), cuando \(X_n=0\).

Por otro lado, si hay algún paquete al final del instante \(n\), \(X_n > 0\), pasan al conmutador en la siguiente ranura \(n+1\), se elimina un paquete al principio de la misma y se añaden los paquetes que lleguen durante esa ranura, \(A_{n+1}\), con sujeción a las limitaciones de capacidad.

Combinando estos casos, obtenemos:

\[\begin{equation*} X_{n+1} = \begin{cases} min(A_{n+1}, K) & \text{ si } X_n = 0\\ min(X_n + A_{n+1} - 1, K) & \text{ si } 0 < X_n \leq K \end{cases} \end{equation*}\]

Asumimos que \(\{A_n, n \geq 1\}\) es una secuencia de variables iid con función de masa de probabilidad dada por:

\[Pr(A_n = k) = a_k, \quad k \geq 0.\]

Bajo esta condición \(\{X_n, n \in \mathbb{N}\}\) es una \(CMTD\) con espacio de estados \(S = \{0, 1, 2,..., K\}\), cuyas probabilidades de transición vienen dadas a continuación para todos los estados \(0 \leq j \leq K\):

Para \(X_n=0 \ (i=0)\):

\[\begin{array}{ll} Pr[X_{n+1} = j | X_n = 0] & = Pr[min(A_{n+1}, K) = j]\\ & = \begin{cases} Pr[A_{n+1} \geq K], \quad \text{ si } j=K\\ Pr[A_{n+1}=j], \quad \text{ si } j<K \end{cases} \\ &= \begin{cases} \sum_{r=K}^{\infty} a_r \quad \text{ si } j=K\\ a_j, \qquad \quad \text{ si } j<K \end{cases} \end{array}\]

Para \(0< X_n=i \leq K\):

\[\begin{array}{ll} Pr[X_{n+1} = j | X_n = i] & = Pr[min(A_{n+1}+X_n-1, K) = j]\\ & = \begin{cases} Pr[A_{n+1} +i-1 \geq K], \quad \text{ si } j=K\\ Pr[A_{n+1}+i-1=j], \quad \text{ si } j<K \end{cases} \\ & = \begin{cases} \sum_{K-i+1}^{\infty} a_r, \qquad \text{ si } j=K\\ a_{j-i+1}, \qquad \qquad \text{ si } i-1 \leq j<K\\ 0, \qquad \qquad \qquad \text{ si } j<i-1 \end{cases} \end{array}\]

Si consideramos:

\[b_j = \sum_{r=j}^{\infty} a_r=1-\sum_{r=0}^{j-1} a_r, \quad j=1,2,...,K\]

la matriz de transiciones de un paso (de dimensión \((K+1) \times (K+1)\) la podemos escribir como:

\[P = \begin{pmatrix} a_0 & a_1 & ... & a_{K-1} & b_K\\ a_0 & a_1 & ... & a_{K-1} & b_K\\ 0 & a_0 & ... & a_{K-2} & b_{K-1}\\ ...&...&...&...&...\\ 0 & 0 & ... & a_0 & b_1 \end{pmatrix}\]

2.3.8 Inventario con desabastecimiento

El gestor de un almacén desea analizar el comportamiento de uno de sus productos en función de la demanda del producto y de la capacidad del almacén.

Consideramos como \(Y_n\) a la variable aleatoria que describe la demanda del producto durante el n-ésimo periodo de tiempo, de forma que:

\[Pr[Y_n = k] = a_k, \quad k=0, 1, 2,... \text{ con } \sum_{k=0}^{\infty} a_k =1\]

Denotamos por \(X_n\) a la variable aleatoria que registra la cantidad de producto almacenado al finalizar el n-ésimo periodo de tiempo, \(A\) el nivel mínimo de almacenaje del producto, y \(B\) el nivel máximo. La política de reposición es la siguiente:

• Si al finalizar un periodo el almacén tiene una cantidad de producto \(X_n\) menor o igual que \(A\), entonces se reabastece hasta \(B\).
• Si al finalizar un periodo el almacén tiene una cantidad de producto mayor que \(A\) y menor o igual a \(B\), entonces no se reabastece y espera hasta el instante de tiempo siguiente.

En esta situación el proceso \(\{X_n, n \in \mathbb{N}\}\) es un proceso estocástico de tiempo discreto

\[\begin{array}{ll} \text{ si } X_n \leq A & \rightarrow X_{n+1} = B - Y_{n+1} \\ \text{ si } A < X_n \leq B & \rightarrow X_{n+1} = X_n - Y_{n+1} \end{array}\]

con espacio de estados \(S = \{B, B-1,..., 1, 0, -1, -2,...\}\), donde los valores negativos indican que la demanda supera a la cantidad almacenada y será servida en instantes posteriores (demanda insatisfecha).

Las probabilidades de transición vienen dadas por:

• si \(i \leq A\)

\[\begin{array}{ll} Pr[X_{n+1} = j | X_{n} =i]&= Pr[B - Y_{n+1} = j] \\ &=Pr[Y_{n+1} = B-j] \\ & = \begin{cases} a_{B-j}, \quad \text{si } B \geq j\\ 0, \qquad \text{ si } B < j \end{cases} \end{array}\]

• si \(A < i \leq B\)

\[\begin{array}{ll} Pr[X_{n+1} = j | X_{n}=i] & = Pr[i - Y_{n+1} = j] \\ &=Pr[Y_{n+1} = i-j] \\ & = \begin{cases} a_{i-j}, \quad \text{ si } i \geq j\\ 0, \qquad \text{ si } i < j \end{cases} \end{array}\]

A modo de ejemplo consideramos \(A = 0\), \(B = 2\), con probabilidades para \(Y_n\) dadas por:

\[Pr[Y_n = 0] = 0.5; \quad Pr[Y_n = 1] = 0.4; \quad Pr[Y_n = 2] = 0.1,\]

entonces la matriz de transición, para el espacio de estados \(S = \{-1, 0, 1, 2\}\), viene dada por:

\[P = \begin{pmatrix} 0 & 0.1 & 0.4 & 0.5\\ 0 & 0.1 & 0.4 & 0.5\\ 0.1 & 0.4 & 0.5 & 0\\ 0 & 0.1 & 0.4 & 0.5 \end{pmatrix}\]

Representamos a continuación este sistema en forma de grafo en la Figura 2.7.

# Definimos estados
estados <- c("-1", "0", "1", "2")
# Matriz de transición 
pmat <- matrix(data = c(0 , 0.1 , 0.4 , 0.5,
                        0 , 0.1 , 0.4 , 0.5,
                        0.1 , 0.4 , 0.5 , 0,
                        0 , 0.1 , 0.4 , 0.5), 
               byrow = TRUE, nrow = 4, 
               dimnames = list(estados, estados))
# CMTD
inventario2 <- new("markovchain", states = estados, 
                 byrow = TRUE, transitionMatrix = pmat, 
                 name = "Inventario 2")
# Verificamos los datos introducidos
inventario2

## Inventario 2 
##  A  4 - dimensional discrete Markov Chain defined by the following states: 
##  -1, 0, 1, 2 
##  The transition matrix  (by rows)  is defined as follows: 
##     -1   0   1   2
## -1 0.0 0.1 0.4 0.5
## 0  0.0 0.1 0.4 0.5
## 1  0.1 0.4 0.5 0.0
## 2  0.0 0.1 0.4 0.5

# Diagrama
plot(inventario2, vertex.color="steelblue", 
     vertex.label.font = 2, 
     vertex.label.color = "white",
     edge.label.size = 0.2,
     edge.arrow.size=0.5, 
     vertex.shape = "rectangle",
     vertex.size = 20)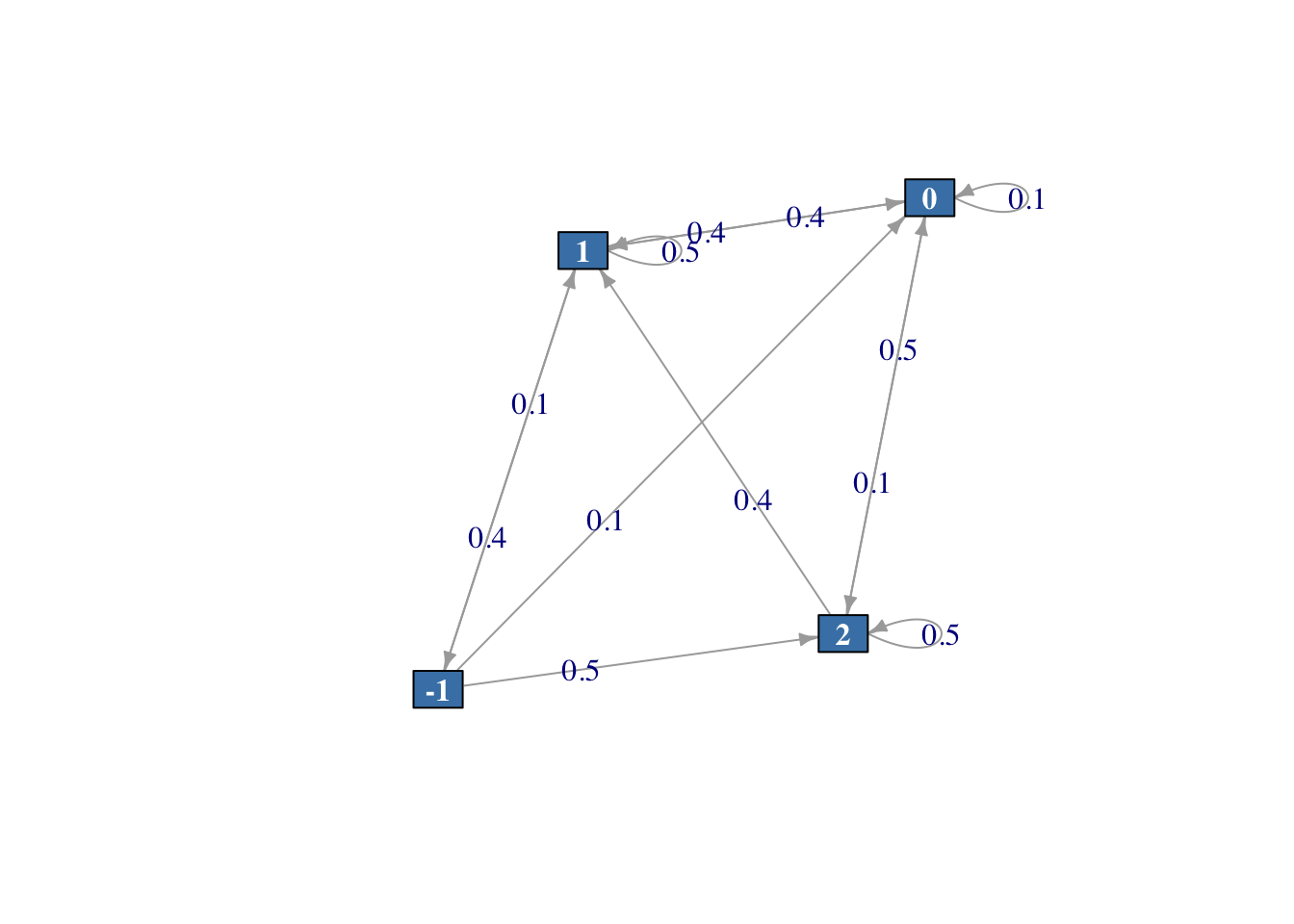

Figura 2.7: Diagrama del sistema del problema de inventario.

2.4 Caracterización de una CMTD

En esta sección estudiamos las principales características de una \(CMTD\) a través de la comunicación entre los diferentes estados de proceso, el número de visitas y los tiempos de ocupación de cada estado, los tiempos a la primera visita, partiendo de un estado, e introducimos la utilización de costes para la evaluación de los sistemas.

En todas las definiciones que presentamos a continuación asumimos que tenemos una \(CMTD\) \(\{X_n, n \in \mathbb{N}\}\) con espacio de estados \(S\) y matriz de transición de un paso \(P\).

2.4.1 Comunicación entre estados

Comenzamos caracterizando los estados de una cadena en función de sus probabilidades de transición.

Definición 2.5 Dados dos estados \(i, j\) de \(S\), se dice que el estado \(j\) es accesible desde el estado \(i\) si existe una transición \(n\) tal que \(p_{ij}(n) > 0\).

Que el estado \(j\) sea accesible desde \(i\) se denota habitualmente como \(i \rightarrow j\).

Definición 2.6 Dados dos estados \(i, j\) de \(S\), se dice que son comunicantes si \(i\) es accesible desde \(j\), y \(j\) es accesible desde \(i\), es decir, existen \(n_1\) y \(n_2\) tal que \(p_{ij}(n_1) > 0\) y \(p_{ji}(n_2) > 0.\)

Que los estados \(i, j\) sean comunicantes se denota habitualmente como \(i \leftrightarrow j\).

Definición 2.7 Un subconjunto de estados \(S_j \subset S\) se denomina clase comunicante del estado \(j\) si todos los estados de ese subconjunto son comunicantes con \(j\).

\[S_j \subset S \text{ es clase comunicante de } j \text{ si } \quad i \leftrightarrow j, \qquad \forall i \in S_j.\]

Definición 2.8 Un estado \(i \in S\) se denomina estado sin retorno cuando no es viable volver a dicho estado tras partir de él, esto es, para \(n \geq 1\), \(p_{ii}(n) = 0.\)

Definición 2.9 Un conjunto de estados \(C \subset S\) se denomina cerrado cuando no es posible pasar de un estado de \(C\) a otro que no esté en \(C\), esto es,

\[\forall i \in C, \quad \forall j \notin C \quad \Rightarrow \quad p_{ij}(n) = 0, \quad n\geq 1\] o lo que es lo mismo,

\[ \sum_{j \in C} p_{ij}=1, \quad \forall i \in C.\]

Esto implica que cuando accedamos a un conjunto cerrado, será imposible salir de él y sólo será factible moverse dentro de él.

Si el conjunto cerrado está compuesto por un único estado \(i\) diremos que ese estado \(i\) es absorbente. Eso implica que si se llega a dicho estado, el proceso se queda estancado en él y ya no es posible moverse a otro estado.

Definición 2.10 Una \(CMTD\) es irreducible cuando todos sus estados están comunicados entre sí, esto es, para cualquier \(i,j \in S\) existe algún instante de tiempo \(n \geq 0\) tal que \(Pr(X_n=j|X_0=i)>0\). Un conjunto de estados en S se dice irreducible cuando no contiene ningún subconjunto cerrado. Si la \(CMTD\) no es irreducible, se llama reducible.

Todos los estados dentro de un conjunto irreducible son del mismo tipo.

Para caracterizar una CMTD mediante la librería markovchain es útil usar la función summary(object) donde ‘object’ identifica el proceso a estudiar.

Ejemplo 2.2 Queremos caracterizar el proceso presentado en el Ejemplo 2.1. Cargamos los datos y ejecutamos la sintaxis a continuación.

# Caracterización
summary(proceso)

## Unnamed Markov chain  Markov chain that is composed by: 
## Closed classes: 
## a b c 
## Recurrent classes: 
## {a,b,c}
## Transient classes: 
## NONE 
## The Markov chain is irreducible 
## The absorbing states are: NONE

A la vista del resultado, concluimos que este proceso es cerrado (todo su espacio de estados es cerrado). Todos sus estados son recurrentes y no tiene estados transitorios (estos conceptos los veremos más adelante). No tiene estados absorbentes y la cadena de Markov es irreducible (todos sus estados están comunicados).

PRACTICA Caracterizar los procesos: Fiabilidad de máquinas,Metereología, Problema de inventario, Planificación de mano de obra, Mercado de valores e Inventario con desabastecimiento.

Ejemplo 2.3 Veamos ahora cómo utilizar la simulación para responder a diferentes preguntas de interés. En concreto, para el ejemplo en la sección Inventario con desabastecimiento (recordemos que se trataba de un almacén que se reabastecía cuando el inventario quedaba por debajo o igual a un nivel mínimo de almacenaje, \(A=0\), y con una política de reabastecimiento que dependía del nivel de almacenaje máximo \(B=2\)), planteamos estas preguntas:

1. Durante las próximas 20 semanas, ¿en cuántas de ellas será preciso reabastecerse?

2. Durante las próximas 20 semanas, ¿cuál es la proporción de semanas en que la demanda no ha sido satisfecha (por rebasar el stock)?

Para responder estas preguntas hay que considerar el proceso \(\{X_n, n \geq 0\}\) y la variable \(Y_n\) que identifica la demanda en la semana \(n\). Planteamos el siguiente algoritmo de simulación.

Algoritmo para simulación de inventario

• Paso 1. Fijar el número de transiciones del proceso, \(n\), e inicializar \(X_0 = 2\) (máximo almacenaje).

Repetir pasos 2 y 3 hasta alcanzar el número de transiciones deseadas.

• Paso 2. Generar \(Y_i\) con el método de la transformada inversa.

• Paso 3. Actualizar el valor \(X_i\) y reabastecer si fuera necesario.

• Paso 4. Devolver la secuencia \(\{X_i, Y_i; i=1,\ldots,n\}\) para estudiar la evolución del sistema y la demanda.

Desarrollemos pues, el algoritmo.

# Inicialización
set.seed(12)
tiempo <- 21 # valor inicial y 20 transiciones
invent <- c()  # vector con los valores de inventario
demanda <- c() # vector con los valores de demanda
A <- 0
B <- 2
##### Configuración metodo transformada inversa ######
# datos uniformes
unif <- runif(tiempo-1)
# Valores posibles para la demanda
valores <- c(0, 1, 2)
# Probabilidades para la demanda
prob <- c(0.5, 0.4, 0.1)
probacum <- cumsum(prob)  # probabilidades acumuladas
# valor inicial del proceso
invent[1] <- 2
demanda[1] <- 0
i<-2
while (i <= tiempo)
{
  # simulamos demanda
  demanda[i] <- valores[min(which(unif[i-1] <= probacum))] 
  # Actualizamos inventario
  ifelse(invent[i-1] <= A, 
         invent[i] <- B - demanda[i], 
         invent[i] <- invent[i-1]-demanda[i])
  # iteración siguiente
  i<-i+1
}
# Devolvemos la secuencia de estados 
inventario2.sim=data.frame(invent,demanda)
head(inventario2.sim)

##   invent demanda
## 1      2       0
## 2      2       0
## 3      1       1
## 4     -1       2
## 5      2       0
## 6      2       0

La estimación del número de semanas que hay que reabastecerse viene dada por el número de simulaciones en las que el nivel de inventario es menor o igual al nivel mínimo de almacenamiento, \(invent=X\leq 0\), es decir

sum(inventario2.sim$invent <= A)

## [1] 3

La proporción de semanas en que la demanda no ha sido satisfecha (por rebasar el stock) corresponde a aquellas en las que la demanda ha superado al inventario,

mean(inventario2.sim$invent <inventario2.sim$demanda)

## [1] 0.1428571

2.4.2 Tiempos de ocupación

Definición 2.11 Sea \(\{X_n, n \geq 0\}\) una \(CMTD\) homogénea con espacio de estados \(S = \{1, 2,...,N\}\), matriz de probabilidades de transición de una paso \(P\), y distribución inicial \(p(0)\). Consideramos la variable aleatoria \(N_j(n)\) como el número de visitas al estado \(j\) en \(n\) transiciones y definimos

\[m_{ij}(n) = E[N_j(n)|X_0 = i]\] como el número esperado de visitas o tiempo de ocupación del estado \(j\) hasta el instante \(n\), partiendo del estado \(i\).

A partir de las cantidades \(m_{ij}(n)\) se puede definir la matriz de tiempos de ocupación hasta un instante \(n\), \(M(n)=(m_{ij}(n))_{ij}\), que se puede calcular a partir de la matriz de transición \(P\) como:

\[\begin{equation} M(n) = \sum_{r=0}^n P^r \tag{2.7} \end{equation}\]

Definición 2.12 Un estado \(i\) se dice que es recurrente si es continuamente revisitado a lo largo de la vida de la cadena, esto es, el número esperado de visitas al estado \(i\) a lo largo de la vida del proceso es infinito, \(m_{ii}=E(N_i|X_0=i)=\infty\). En otro caso, cuando sólo se accede un número finito de veces, se dice que es transitorio. Un estado transitorio sólo será accesible durante un cierto periodo de tiempo, tras el cual dicho estado ya no será revisitado nunca más.

Ejemplo 2.4 Volvemos sobre el Ejemplo 2.1 para calcular los tiempos de ocupación durante un periodo continuado de 10 transiciones. Para ello utilizamos la Ecuación (2.7) con \(n=10\).

## Simulación de los tiempos de ocupación (número de visitas a un estado)
# Número de estados del proceso
nestat <- dim(proceso)
# Estados
nombres<- names(proceso)
# Generamos la matriz de ocupaciones
# el primer elemento es la matriz identidad: p^0
mocupa <- diag(nestat)
  dimnames(mocupa) <- list(nombres, nombres)
# Bucle de cálculo de los tiempos de ocupación
P=proceso[1:nestat,1:nestat] # matriz de transición
for (i in 1:10)
{
   mocupa <- mocupa + ptran.n(P,i)
}
mocupa

##          a        b        c
## a 4.531739 1.248415 5.219845
## b 3.555292 1.955489 5.489220
## c 3.858338 1.046384 6.095278

Podemos ver cómo el número esperado de visitas al estado \(c\) partiendo del estado \(b\) en las próximas 10 transiciones es casi de 7 (6.86). Sin embargo, si partimos del estado \(b\), en 10 transiciones sólo esperamos volver a dicho estado 1 vez.

Definamos una función para obtener la matriz de tiempos de ocupación (o número esperado de visitas) durante un periodo de duración de \(n\) unidades de tiempo.

# Función para calcular los tiempos de ocupación en un periodo [0,n]
mocupa.proceso <- function(proceso, n)
{
  # Número de estados del proceso
  nestat <- dim(proceso)
  # Estados
  nombres<- names(proceso)
  # Generamos la matriz de ocupaciones
  mocupa <- diag(nestat)
  dimnames(mocupa) <- list(nombres, nombres)
#  mocupa <- matrix(rep(0, nestat*nestat),
#                 nrow = nestat, dimnames = list(nombres, nombres))
  # Bucle de cálculo de los tiempos de ocupación
  P=proceso[1:nestat,1:nestat]
  for (i in 1:n)
   mocupa <- mocupa + ptran.n(P,i)
  
  return(mocupa)
}

PRACTICA Obtener y caracterizar la matriz del número esperado de visitas en 20 transiciones para los procesos: Fiabilidad de máquinas,Metereología, Problema de inventario, Planificación de mano de obra y Mercado de valores.

2.4.3 Análisis de costes

Una aplicación muy habitual de los tiempos de ocupación es directa en los denominados modelos de costes, que describimos brevemente, y que pueden estar vinculados en situaciones específicas a costes, pero también a beneficios, pérdidas, etc..

Sea \(X_n\) el estado del sistema en el tiempo \(n\). Asumimos que \(\{X_n, n \geq 0 \}\) es una \(CMTD\) con espacio de estados \(S =\{1, 2,...,N\}\), matriz de transición \(P\), y matriz de tiempos de ocupación \(M(n)\).

En esta situación, hablamos de que cada visita a cierto estado \(i\) tiene un coste aleatorio asociado \(C(i)\), y el coste esperado por cada visita al estado \(i\) viene dado por \(c(i) = E[C(i)]\). Definimos la matriz de costes esperados asociados a los estados, como \(\mathbf{c}\), de dimensión \(N\times 1\), como:

\[\mathbf{c}' = (c(1),c(2),\ldots,c(N))\]

Así mismo, hablamos del coste \(C(X_r)\) en el que incurre el sistema en un instante concreto \(r\), y \(\sum_{r=0}^n C(X_r)\) el coste acumulado desde el inicio del proceso hasta llegar al instante \(n\). Entonces el coste esperado total (CET) asociado al funcionamiento del sistema hasta llegar al instante \(n\) se calculará como

\[CET=E\left[\sum_{r=0}^n C(X_r)\right]\]

Definimos el coste esperado total hasta el instante \(n\) partiendo del estado \(i\), \(g(i,n)\), como:

\[g(i,n) = E\left[\sum_{r=0}^n C(X_r)| X_0 = i \right]\]

y construimos la matriz de costes totales sobre un horizonte finito (CTHF) hasta el instante \(n\), \(\mathbf{g}(n)\), de dimensión \(N \times 1\), a través de estos costes esperados partiendo de cualesquier estado \(i \in S\), como

\[\mathbf{g}(n)' = (g(1,n),g(2,n),\ldots,g(N,n))\]

Definición 2.13 Si vinculado al funcionamiento de un sistema CMTD queremos calcular el coste esperado total sobre un horizonte finito hasta un instante \(n\), (CTHF), basta multiplicar la matriz de tiempos de ocupación hasta el instante \(n\), \(M(n)\), por la matriz de costes esperados asociados a los estados del sistema, \(\mathbf{c}\), esto es, resolver la Ecuación (2.8).

\[\begin{equation} \mathbf{g}(n) = M(n) \cdot \mathbf{c} \tag{2.8} \end{equation}\]

Ejemplo 2.5 Volvamos al proceso de inventario presentado en el Problema de inventario con espacio de estados \(\{2,3,4,5\}\). Supongamos que la empresa compra PCs por 1500 euros y los vende por 1750 euros. Además el coste de almacenamiento semanal es de 50 euros por cada unidad que está en la tienda al inicio de una semana. Queremos calcular los ingresos netos que la tienda espera obtener durante las próximas 10 semanas, suponiendo que comienza con cinco PCs en stock al inicio del periodo.

En esta situación, estamos interesados en los ingresos, por lo que definimos \(c(i)\) como los ingresos netos que se obtienen en una semana cualquiera en la que hay \(i\) PCs al principio de la semana. Sabemos que los costes de almacenamiento de \(i\) PCs es \(50i\). Las ganancias provendrán de los PCs que se hayan vendido. Si \(D_n\) es la demanda durante una semana cualquiera \(n\), el número esperado de PCs vendidos durante esa semana será \(E[min(i, D_n)]\). Así, los ingresos netos previstos para una semana cualquiera \(n\) en la que se tienen \(i\) PCs almacenados al inicio, \(c(i)\), provendrán de los ingresos por ventas menos los gastos de almacenaje, esto es,

\[c(i) = (1750-1500)E[min(i, D_n)] -50i, \quad 2 \leq i \leq 5\]

Necesitamos pues, obtener el valor de \(E[min(i, D_n)]\), para cada valor de \(i\). Veamos cómo hacerlo, tanto de forma teórica como mediante simulación. Denotemos por \(Z_{i,n} = min(i, D_n),\) para \(i=2, 3, 4, 5\) de forma que:

\[\begin{equation*} Z_{i,n} = \begin{cases} i & \text{ si } i <D_n \\ D_n & \text{ si } i \geq D_n \end{cases} \end{equation*}\]

de esta forma tenemos que su valor esperado vendrá dado por:

\[E[Z_{i,n}] = i \cdot Pr[i < D_n] + \sum_{d=0}^{i} d \cdot Pr(D_n=d).\]

Recordando que \(D_n\sim Pois(3)\) en el ejemplo original, para \(i=2\) la expresión anterior da lugar a:

\[\begin{eqnarray*} E[Z_{2,n}] &= 2 \cdot Pr[D_n > 2] + 0 \cdot Pr[D_n = 0] + 1 \cdot Pr[D_n =1] +2 \cdot Pr(D_n=2) \\ &= 2 \cdot (1-Pr(D_n \leq 2)) + 1 \cdot Pr[D_n =1] + 2 \cdot Pr(D_n=2) \\ &= 2 \cdot 0.5768 +0.1494 +2 \cdot 0.2240 = 1.751 \end{eqnarray*}\]

de donde calculamos los ingresos \(c(2)\) con la ecuación anterior. \[c(2) = 250 \cdot 1.751 -50 \cdot 2 = 337.75\] Hacemos fácilmente los cálculos para todos los estados:

estados=2:5
lambda=3   # Poisson para la demanda
# número esperado de ventas
ez=c()
for(i in estados){
ez[i-1]=i*(1-ppois(i,lambda))+sum((0:i)*dpois(0:i,lambda))
}
ingresos=250*ez-50*estados;ingresos

## [1] 337.7662 431.9686 470.1607 466.3449

Y obtenemos

\[\mathbf{c} = \begin{pmatrix} 337.75 \\ 431.95 \\ 470.15 \\ 466.23 \end{pmatrix}\]

Con esta matriz y la matriz de ocupación hasta el instante \(n=10\) podemos calcular los ingresos netos totales esperados durante las próximas \(n=10\) semanas, sea cual sea el estado inicial del sistema:

\[g(10)=M(10) \cdot c\] que calculamos a continuación:

c=matrix(round(ingresos,2), ncol=1)
M10=mocupa.proceso(inventario,10)
g=M10 %*% c
g

##           [,1]
## 2 PCs 4736.876
## 3 PCs 4819.392
## 4 PCs 4847.637
## 5 PCs 4842.589

y que nos permite extraer los ingresos netos totales esperados asumiendo que el periodo inicia con \(i=5\) PCs en tienda, esto es, como $g(5,10)=$4842.59 euros.

Los valores de \(c\) se pueden aproximar mediante simulación sin necesidad de calcularlos de forma teórica. A continuación se presenta el código necesario para realizar la simulación. Concretamente definimos una función que depende del valor del estado inicial \(i\).

# simulador del valor esperado del número esperado de ventas
c.sim <- function(estado, nsim)
{
  # estado: estado inicial del sistema
  # nsim: nº simulaciones para la aproximación
  
  # Simulamos valores del mínimo entre i y D_n
  datos <- data.frame(rsim = rpois(nsim, 3), rdos <- rep(estado, nsim))
  minimo <-apply(datos, 1 ,min) # Mínimo por filas
  # Valor esperado min(i,D_n)
  esperanza <- mean(minimo)
  # coste
  coste <- round(-50*estado+250*esperanza, 2)
  return(coste)
}

Aproximamos pues por simulación, los valores de la matriz \(c\) con \(nsim=1.000.000\) simulaciones

nsim <- 1000000
set.seed(12)
c.s=matrix(c(c.sim(2, nsim),c.sim(3, nsim),
      c.sim(4, nsim),c.sim(5, nsim)),ncol=1)
c.s

##        [,1]
## [1,] 337.66
## [2,] 431.61
## [3,] 470.28
## [4,] 466.69

Como se puede ver, la simulación funciona bastante bien para aproximar el vector \(c\); resolvamos pues los cálculos de \(g(5,10)\) con estos valores, que de nuevo aproximarán las cantidades que buscamos.

# matriz M
Mmat <- mocupa.proceso(inventario, 10)
# vector g
beneficio <- Mmat%*%c.s
beneficio

##           [,1]
## 2 PCs 4738.291
## 3 PCs 4820.502
## 4 PCs 4849.143
## 5 PCs 4844.266

Mientras que teóricamente obteníamos unos ingresos esperados de 4842.59€, con la simulación obtenemos una aproximación de 4844.27€.

2.4.4 Tiempos de primer paso

Definición 2.14 Sea \(\{X_n, n \geq 0\}\) una \(CMTD\) homogénea con espacio de estados \(S = \{1, 2,...,N\}\). Se define el tiempo de primer paso o tiempo de primera visita al estado \(j\) partiendo del estado \(i\), \(T_{ij}\), como el mínimo número de transiciones necesarias para alcanzar el estado \(j\) partiendo del estado inicial \(i\), es decir:

\[T_{ij} = \underset{n}{min}\{n > 0, X_n = j | X_0 = i\}\]

En ocasiones interesará sin embargo el tiempo de primer paso de un estado a un conjunto de estados \(A\):

\[T_{iA} = \underset{n}{min}\{n > 0, X_n \in A | X_0 = i\}.\]

Para obtener los tiempos esperados de recurrencia \(f=(f_{11},...,f_{NN})\) para el espacio de estados \(S=\{1,...,N\}\), utilizamos la función meanRecurrenceTime(proceso) de la librería markovchain.

Para obtener los tiempos esperados de primer paso por un estado \(j\) desde cualquier estado de \(S\), podemos utilizar la función meanFirstPassageTime(proceso,destination=j) de la librería markovchain. Si queremos calcular la matriz de tiempos esperados para llegar a cualquier estado desde cualquier estado, basta utilizar meanFirstPassageTime(proceso).

En caso de que no podamos utilizar la función meanFirstPassageTime para el cálculo del tiempo esperado de primer paso, podemos utilizar la propiedad que pasamos a describir.

Definición 2.15 Sea \(\{X_n, n \geq 0\}\) una \(CMTD\) con espacio de estados \(S = \{1, 2,...,N\}\). Si estamos interesados en obtener el tiempo esperado de primer paso para el estado \(j\) desde cualquier estado \(i\), dado por:

\[v_{ij} = E(T_{ij}), \quad \text{ con } T_{ij} = \underset{n}{min}\{n > 0, X_n = j | X_0 = i\}\]

y construimos la matriz de dimensión \((N-1) \times 1\) \(\mathbf{v_j'}=(v_{1j},...,v_{j-1,j},v_{j+1,j},...,v_{Nj})\)
basta con resolver el sistema:

\[\begin{equation} [\mathbf{I} - P_{-j}]\mathbf{v_j} = \mathbf{1} \tag{2.9} \end{equation}\]

donde

• \(P_{-j}\) es la matriz de transición eliminando la fila y columna del estado \(j\),
• \(\mathbf{1}\) es un vector de unos, de dimensión \(N-1\),
• \(\mathbf{I}\) es una matriz diagonal de las mismas dimensiones que \(P_{-N}\).

Esta ecuación se puede generalizar para obtener los tiempos esperados de primer paso desde un estado \(i\) hasta cualquier subconjunto de estados \(S_c \subset S\).

Función para obtener los tiempos esperados de primer paso

Como alternativa a la función definida en markovchain, programamos a continuación una función genérica para poder obtener los tiempos esperados de primer paso, dependiente de dos parámetros:

• proceso: \(CMTD\) que describe el sistema a estudio
• estado: estado o conjunto de estados que se desean alcanzar, partiendo desde cualquier estado inicial que no está en este conjunto.

# Función para obtener el tiempo esperado de primer paso por "estado"
# (equivalente a meanFirstPassageTime de markovchain)
tiempo.pp <- function(proceso, estado)
{
  # estados del proceso
  estados <- states(proceso)
  numestados <- length(estados)
  # posición de los estados deseados
  lestat <- length(estado)
  pos <- which(estados %in% estado)
  # matriz P_N
  P_N <- proceso[-pos,-pos]
  # vector de unos
  vector.1 <- matrix(rep(1, numestados-lestat), ncol=1)
  # sistema de ecuaciones
  sistema <- diag(numestados-lestat) - P_N
  # solución del sistema
  solucion <- solve(sistema, vector.1)
  return(solucion)
}

Definición 2.16 Sea \(\{X_n, n \geq 0\}\) una \(CMTD\) homogénea con espacio de estados \(S = \{1, 2,...,N\}\). Se definen las probabilidades de primera visita o primer paso del estado \(i\) al \(j\) en \(n\) transiciones, con \(f_{ij}(n)\),

\[\begin{eqnarray*} f_{ij}(n) &=& Pr[X_n = j, X_{n-1} \neq j,\ldots, X_1 \neq j | \quad X_0 = i] \\ &=& Pr(T_{ij}=n), \quad n \geq 0 \end{eqnarray*}\]

donde por convenio \(f_{ij}(0) = 0.\)

Podemos obtener la distribución de probabilidad asociada al tiempo de primer paso del estado \(j\) desde el estado \(i\) en \(n\) transiciones, \(f_{ij}(n)\), con la función firstPassageMultiple(proceso,state=i,set=j,n=n).

Definición 2.17 Si \(T_{ii}\) denota el tiempo del primer retorno, o tiempo de recurrencia al estado \(i\), entonces se dice que el estado \(i\) es recurrente si \(f_{ii}=Pr(T_{ii}<\infty)=1\), es decir, si el sistema se inicia en él, pueda volver a él. Es transitorio si \(f_{ii}<1\).

Ejemplo 2.6 Analizamos los tiempos de primer paso, tiempos de recurrencia y probabilidades de primer paso sobre el proceso presentado en el Ejemplo 2.1. Estamos interesados en saber cuándo alcanzaremos el estado “b” partiendo desde cualquier estado en el momento inicial.

Comenzamos calculando los tiempos de primer paso utilizando las dos funciones consideradas, la propia y la de markovchain.

# Tiempo de primer paso partiendo del estado "b"
# libreria
meanFirstPassageTime(proceso, "b")

##        a        c 
## 6.363636 8.181818

# definida por nosotros
tiempo.pp(proceso, "b")

##       [,1]
## a 6.363636
## c 8.181818

Podemos ver que ambas funciones proporcionan el mismo resultado. Si comenzamos en el estado “a” tardaremos en promedio seis transiciones para alcanzar por primera vez el estado “b,” mientras que si empezamos en el estado “c” tardaremos 8 transiciones en alcanzar el estado “b.”

Si deseamos la matriz del valor esperado del primer paso en cualquier estado basta con ejecutar

meanFirstPassageTime(proceso)

##          a        b        c
## a 0.000000 6.363636 1.688312
## b 2.636364 0.000000 1.168831
## c 1.818182 8.181818 0.000000

Obtenemos ahora el tiempo de primer paso (utilizando la función programada) y la probabilidad de primer paso de pasar del estado \(b\) a cualquiera de los estados \(a\) o \(c\) en 10 transiciones (\(A = \{a, c\}\))

# Tiempo esperado e primer paso de "b" a "A"
tiempo.pp(proceso,c("a","c"))

##      [,1]
## [1,]    1

# Probabilidad de primer paso de "b" a "A"
firstPassageMultiple(proceso, "b", c("a","c"), 10)

##             set
## 1  1.0000000000
## 2  0.5450000000
## 3  0.2597500000
## 4  0.1091375000
## 5  0.0479968750
## 6  0.0211430938
## 7  0.0093898422
## 8  0.0041868540
## 9  0.0018726328
## 10 0.0008392372

Se espera poder pasar de \(b\) a \(A\) en una transición (lógico puesto que A es el conjunto complementario a \(b\) en el conjunto de estados), mientras que la probabilidad de pasar del estado \(b\) al conjunto \(A\) en dos transiciones es de \(0.55\) y tan solo de \(0.0008\) en 10 transiciones.

En cuanto a los tiempos de recurrencia, tenemos:

# Tiempo de recurrencia
meanRecurrenceTime(proceso)

##        a        b        c 
## 2.700000 9.000000 1.928571

Podemos ver que una vez hemos pasado por el estado “b” tardamos 9 transiciones en volver a él. Calculamos ahora la probabilidad de recurrencia en 10 transiciones.

# Probabilidad de recurrencia en 10 pasos
firstPassageMultiple(proceso, "b", "b", 10)

##           set
## 1  0.00000000
## 2  0.03000000
## 3  0.15450000
## 4  0.10597500
## 5  0.09746625
## 6  0.08295844
## 7  0.07195424
## 8  0.06211757
## 9  0.05368795
## 10 0.04638892

Si iniciamos el proceso en el estado “b” la probabilidad de volver a dicho estado es muy baja en cualquiera de las 10 primeras transiciones. La probabilidad de volver en 3 transiciones es de 0.15, pero de volver en 10 transiciones es de 0.046.

¿Qué implicaciones prácticas tienen los análisis realizados en el proceso estudiado?

Ejemplo 2.7 Consideramos el proceso que ya vimos sobre Fiabilidad de máquinas. Supongamos que en el instante inicial (dia 0) las dos máquinas están “On,” y que deseamos calcular el tiempo esperado hasta que las dos máquinas estén “Off” por primera vez.

Si \(Y_n\) es el proceso que representa el número de máquinas que están “On,” con espacio de estados \(S = \{0, 1, 2\}\), estamos interesados en calcular el tiempo esperado para llegar a \(Y_n = 0\) (dos máquinas “Off”) partiendo de \(Y_0 = 2\) (dos máquinas “On”). Utilizamos la función propia estableciendo el estado objetivo.

# Tiempo de primer paso para acabar en el estado "0"
tiempo.pp(fiabilidad, "0")

##       [,1]
## 1 2450.990
## 2 2451.485

El tiempo esperado para que las dos máquinas estén en estado “Off” comenzando con ambas en el estado “On” es 2451.5, que expresado en años será \(2451.5/365 = 6.71\) años.

Ejemplo 2.8 Consideramos el proceso ya presentado sobre Planificación de mano de obra. Deseamos el tiempo medio de permanencia en la empresa para un empleado recién reclutado. Recordemos que un nuevo empleado siempre empieza en el nivel “1.” Definamos un proceso \(Y_n\) que representa el nivel de un empleado novel en la semana n-ésima, proceso que puede tomar los valores \(S = \{0, 1, 2, 3, 4\}\), donde \(Y_n=0\) significa que deja la empresa en n semanas después de empezar. En esta situación el proceso \(\{Y_n, n \geq 0\}\) es una \(CMTD\) con espacio de estados \(S = \{0, 1, 2, 3, 4\}\) y matriz de probabilidades de transición calculadas a partir de las probabilidades que se daban en el desarrollo de Planificación de mano de obra y teniendo en cuenta que si está fuera de la empresa, a la semana siguiente también lo estará:

\[P = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0.02 & 0.98 & 0.03 & 0 & 0\\ 0.008 & 0 & 0.982 & 0.01 & 0\\ 0.02 & 0 & 0 & 0.975 & 0.005\\ 0.01 & 0 & 0 & 0 & 0.99 \end{pmatrix}\]

Creamos la estructura del sistema:

# Definimos estados
estados <- c("0", "1", "2", "3", "4")
# Matriz de transición 
pmat <- matrix(data = c(1, 0, 0, 0, 0,  
                        0.02, 0.95, 0.03, 0, 0, 
                        0.008, 0, 0.982, 0.01, 0,   
                        0.02, 0, 0, 0.975, 0.005,
                        0.01, 0, 0, 0, 0.99), 
               byrow = TRUE, nrow = 5, 
               dimnames = list(estados, estados))
# CMTD
planificacion2 <- new("markovchain", states = estados, 
                 byrow = TRUE, transitionMatrix = pmat, name = "planificacion")
# Verificamos los datos introducidos
planificacion2

## planificacion 
##  A  5 - dimensional discrete Markov Chain defined by the following states: 
##  0, 1, 2, 3, 4 
##  The transition matrix  (by rows)  is defined as follows: 
##       0    1     2     3     4
## 0 1.000 0.00 0.000 0.000 0.000
## 1 0.020 0.95 0.030 0.000 0.000
## 2 0.008 0.00 0.982 0.010 0.000
## 3 0.020 0.00 0.000 0.975 0.005
## 4 0.010 0.00 0.000 0.000 0.990

# y describimos el sistema
summary(planificacion2)

## planificacion  Markov chain that is composed by: 
## Closed classes: 
## 0 
## Recurrent classes: 
## {0}
## Transient classes: 
## {1},{2},{3},{4}
## The Markov chain is not irreducible 
## The absorbing states are: 0

En este caso el estado “0” es absorbente (cuando es despedido, ya no vuelve), y el resto de estados son transitorios. Al tener un estado absorbente, no es irreducible y no se puede aplicar la función meanFirstPassageTime() para calcular los tiempos de primer paso esperados. Usamos pues, la función que hemos programado:

# Tiempo esperado para llegar a estado 0
tiempo.pp(planificacion2, "0")

##        [,1]
## 1  73.33333
## 2  88.88889
## 3  60.00000
## 4 100.00000

Puesto que el nuevo empleado comienza siempre en el nivel “1,” el tiempo esperado para que abandone la empresa es de 73.33 semanas (el proceso se mide en semanas), lo que equivale a 1.4 años (\(73.33/52\)).

2.5 Comportamiento a largo plazo

En está sección estamos interesados en estudiar el comportamiento a largo plazo o asintótico de una \(CMTD\), es decir, el comportamiento cuando \(n \rightarrow \infty\).

La distribución estacionaria \(\{\pi_1,..., \pi_N\}\) de una CMTD \(\{X_n, n \geq 0\}\), con espacio de estados \(S =\{1, 2,..., N\}\) verifica que:

\[Pr(X_n=i)=\pi_i, \forall i \in S, \ n \geq 0.\]

Si existe la distribución a largo plazo de un proceso CMTD \(\{X_n, n \geq 0\}\), con espacio de estados \(S =\{1, 2,..., N\}\) y matriz de probabilidades de transición \(P\), la denominamos distribución límite o distribución en estado estacionario, y la denotamos por:

\[\pi = [\pi_1, \pi_2,...,\pi_N]\]

donde

\[\pi_j = \underset{n \rightarrow \infty}{lim} Pr[X_n = j], \quad j \in S\] Si existe la distribución límite o en estado estacionario, dicha distribución es la distribución estacionaria.

Si existe la distribución límite de un proceso CMTD \(\{X_n, n \geq 0\}\), con espacio de estados \(S =\{1, 2,..., N\}\) y matriz de probabilidades de transición \(P\), entonces las probabilidades \(\pi_j\) satisfacen la siguiente ecuación:

\[\pi_j = \sum_{i=1}^N \pi_i p_{ij}, \quad \forall j \in S,\] donde \(p_{ij}\) son las probabilidades de transición (en la matriz \(P\)). Esta propiedad en formato matricial da lugar a la ecuación de balance o del estado estacionario, que viene dada por:

\[\begin{equation} \pi = \pi \cdot P, \qquad \text{ con } \tag{2.10} \end{equation}\]

junto con la restricción de normalización

\[\sum_{j=1}^N \pi_j = 1.\]

Definición 2.18 Sea \(\{X_n, n \geq 0\}\) una \(CMTD\), con \(N_j(n)\) el número de visitas o tiempo de ocupación del estado \(j\). La ocupación del estado \(j\) se define como la proporción de visitas al estado \(j\) (o proporción del tiempo de ocupación que el sistema está en \(j\)) en el largo plazo (\(n \rightarrow \infty\)):

\[\begin{equation} \pi_j=lim_{n \rightarrow \infty} \frac{E[N_j(n)|X_0=i]}{n+1} \tag{2.11} \end{equation}\]

Si existe esta distribución de ocupación, entonces satisface las ecuaciones de balance y de normalización en (2.10).

Teorema 2.1 Una CMTD con espacio de estados finitos y que es irreducible tiene una única distribución estacionaria, es decir, sólo hay una solución normalizada de la ecuación de balance.

Una CMTD con espacio de estados finitos y que es irreducible tiene una única distribución de ocupación y es igual a la distribución estacionaria.

Introducimos ahora el concepto de periodicidad, que nos ayudará a decidir cuándo existe la distribución estacionaria.

Definición 2.19 Sea la \(CMTD\) \(\{X_n, n \geq 0\}\) con espacio de estados \(S =\{1, 2,..., N\}\) y \(d\) el entero más grande tal que para cualquier estado \(i \in S\)

\[\text{si } Pr[X_n = i | X_0 = i] >0 \Rightarrow n \text{ es múltiplo de } d,\]

Se dice entonces que dicha \(CMTD\) es periódica con periodo \(d\) si \(d>1\), y aperiódica si \(d = 1\).

Así, una CMTD con periodo \(d\) puede volver a su estado inicial sólo en los instantes \(d, 2d, 3d, ...\). En consecuencia, en las CMTD irreducibles es suficiente encontrar el periodo \(d\) para cualquier estado \(i \in S\), puesto que será el mismo para todos los estados, con lo que encontrar el periodo en CMTD irreducibles será sencillo.

En particular, si \(p_{ii}>0\) para cualquier \(i\in S\) (todos los estados son recurrentes) de una CMTD irreducible, entonces \(d=1\) y la CMTD será aperiódica.

Teorema 2.2 Una CMTD con espacio de estados finitos, irreducible y aperiódica tiene una única distribución límite o en el estado estacionario, que coincide pues con la distribución estacionaria y también con la de los tiempos de ocupación.

La distribución límite o en estado estacionario de una CMTD reducible no es única y depende del estado inicial de la cadena.

Podemos estudiar la periocidad de un sistema mediante la función period() de la librería markovchain.

La función steadyStates() de la librería markovchain nos devuelve la distribución estacionaria de una \(CMTD\).

Ejemplo 2.9 Analizamos el sistema presentado en el Ejemplo 2.1 para obtener la distribución estacionaria:

period(proceso)

## [1] 1

# Distribución estacionaria
steadyStates(proceso)

##              a         b         c
## [1,] 0.3703704 0.1111111 0.5185185

Obtenemos de esta forma las probabilidades asintóticas de estar en cada uno de los estados. Vemos pues, que a la larga lo más probable es que nos encontremos en el estado ‘c,’ y lo menos probable es estar en el estado ‘b.’

Definición 2.20 Si \(i\) es un estado recurrente y existe la distribución estacionaria, entonces el valor esperado del tiempo de recurrencia es el inverso de la probabilidad de \(i\) según la distribución estacionaria, es decir,

\[\begin{equation} E[T_{ii}] = 1/\pi_i. \tag{2.12} \end{equation}\]

Tenemos un resultado adicional sobre el comportamiento de los costes en el estado estacionario.

Definición 2.21 Si \(c(i)\) es el coste esperado en el que incurrimos cuando visitamos el estado \(i \in S\), de una CMTD irreducible con distribución de ocupación \(\pi\), entonces el coste esperado por unidad a largo plazo (en el estado estacionario) viene dado por:

\[g= \sum_{j\in S} \pi_j \ c(j).\]

Ejemplo 2.10 Para el proceso descrito en la sección Telecomunicaciones, en el que los paquetes de datos que se generan en el instante (ranura) \(n\), \(A_n \sim Po(1)\), se almacenaban en un buffer de capacidad \(K=7\), que se van eliminando conforme a cierta estrategia. Interesados en el proceso \(\{X_n, n\geq 0\}\) que describe el número de paquetes en el buffer al final de la n-ésima ranura, con espacio de estados \(S=\{0, 1,..., 7\}\) y matriz de probabilidades de transición:

\[P = \begin{pmatrix} 0.3679 & 0.3679 & 0.1839 & 0.0613 & 0.0153 & 0.0031 & 0.0005 & 0.0001\\ 0.3679 & 0.3679 & 0.1839 & 0.0613 & 0.0153 & 0.0031 & 0.0005 & 0.0001\\ 0.0 & 0.3679 & 0.3679 & 0.1839 & 0.0613 & 0.0153 & 0.0031 & 0.0006\\ 0.0 & 0.0 & 0.3679 & 0.3679 & 0.1839 & 0.0613 & 0.0153 & 0.0037\\ 0.0 & 0.0 & 0.0& 0.3679 & 0.3679 & 0.1839 & 0.0613 & 0.0190\\ 0.0 & 0.0 & 0.0& 0.0& 0.3679 & 0.3679 & 0.1839 & 0.0803\\ 0.0 & 0.0 & 0.0& 0.0& 0.0& 0.3679 & 0.3679 & 0.2642\\ 0.0 & 0.0 & 0.0& 0.0& 0.0& 0.0& 0.3679 & 0.6321\\ \end{pmatrix}\]

En esta situación estamos interesados en analizar las siguientes características del estado estacionario del proceso \(X_n\):

1. Periodo del proceso.
2. Fracción de tiempo en que el buffer estará lleno.
3. Número esperado de paquetes que esperan en el buffer.

Definamos la estructura del proceso para la librería markovchain, y pidamos la distribución estacionaria.

# Estructura del proceso
# Definimos estados
estados <- as.character(0:7)
# Matriz de transición 
pmat <- matrix(data = c(0.3679, 0.3679, 0.1839, 0.0613, 0.0153, 
                        0.0031, 0.0005, 0.0001,
0.3679, 0.3679, 0.1839, 0.0613, 0.0153, 0.0031, 0.0005, 0.0001,
0.0, 0.3679, 0.3679, 0.1839, 0.0613, 0.0153, 0.0031, 0.0006,
0.0, 0.0, 0.3679, 0.3679, 0.1839, 0.0613, 0.0153, 0.0037,
0.0, 0.0, 0.0, 0.3679, 0.3679, 0.1839, 0.0613, 0.0190,
0.0, 0.0, 0.0, 0.0, 0.3679, 0.3679, 0.1839, 0.0803,
0.0, 0.0, 0.0, 0.0, 0.0, 0.3679, 0.3679, 0.2642,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.3679, 0.6321), 
               byrow = TRUE, nrow = 8, 
               dimnames = list(estados, estados))
# CMTD
teleco <- new("markovchain", states = estados, 
                 byrow = TRUE, transitionMatrix = pmat, 
              name = "Telecomunicaciones")
# Revisamos si la CMTD es irreducible
summary(teleco)

## Telecomunicaciones  Markov chain that is composed by: 
## Closed classes: 
## 0 1 2 3 4 5 6 7 
## Recurrent classes: 
## {0,1,2,3,4,5,6,7}
## Transient classes: 
## NONE 
## The Markov chain is irreducible 
## The absorbing states are: NONE

# Periodo del sistema
period(teleco)

## [1] 1

# Distribución estacionaria
steadyStates(teleco)

##               0         1         2         3         4         5         6         7
## [1,] 0.06820411 0.1171835 0.1331324 0.1360701 0.1363485 0.1363554 0.1363497 0.1363562

Tenemos que la CMTD es irreducible, luego por los resultados teóricos tiene una única distribución estacionaria, que coincidirá con la distribución límite y con la distribución de los tiempos de ocupación.

Que el buffer esté lleno significa que nos encontramos en el estado “7,” y al ser la distribución estacionaria la del tiempo de ocupación, tenemos que la fracción de tiempo en que el buffer está lleno es del 13.64%.

El número esperado de paquetes en el buffer en el estado estacionario es un valor esperado calculado con la distribución límite/estacionaria, que al ser discreta se calcula fácilmente a partir de las distribución estacionaria obtenida, esto es,

estados <- 0:7
distribucion <- steadyStates(teleco)
# Valor esperado
sum(estados*distribucion)

## [1] 3.791421

Por lo tanto, a largo plazo se espera que el buffer esté a un poco más de la mitad de su capacidad.

Ejemplo 2.11 Consideramos el proceso de Planificación de mano de obra, donde suponemos que la empresa tiene 70 empleados cuyo nivel no cambia a lo largo del tiempo. Supongamos que los gastos de nómina semanales por persona son de 400 dólares para el grado 1, 600 dólares para el grado 2, 800 dólares para grado 3, y $1000 para el grado 4. Estamos interesados en calcular los gastos semanales promedio por empleado.

Aplicando el resultado en la Definición 2.21, comprobemos que el proceso es irreducible y procedamos a aplicar la fórmula correspondiente, si es el caso.

# ¿el proceso es irreducible?
summary(planificacion)

## planificacion  Markov chain that is composed by: 
## Closed classes: 
## 1 2 3 4 
## Recurrent classes: 
## {1,2,3,4}
## Transient classes: 
## NONE 
## The Markov chain is irreducible 
## The absorbing states are: NONE

# Vector de costes
costes <- c(400, 600, 800, 1000)
# distribución estado estacionario
distribucion <- steadyStates(planificacion)
# gastos esperados por semana
cat("\n Gastos semanales:",sum(distribucion*costes))

## 
##  Gastos semanales: 618.1818

Por tanto, los gastos semanales promedio por trabajador son de 618.20 dólares, lo que multiplicado por el número de empleados (70) supone 43274 dólares.

2.6 Estudio de caso

Veamos por último, una aplicación completa del análisis de una CMTD.

Sabemos que en cada idioma las frecuencias de transición entre vocales y consonantes son diferentes. A partir de análisis recurrentes con textos de dos idiomas hemos identificado las probabilidades de transición entre vocales y consonantes en cada uno, estados=(vocal,consonante), y que vienen dadas a continuación.

\[p1=\left(\begin{matrix} 0.51 & 0.49 \\ 0.90 & 0.10 \end{matrix} \right), \qquad p2=\left(\begin{matrix} 0.25 & 0.75 \\ 0.30 & 0.70 \end{matrix} \right)\]

Definimos primero los procesos para la librería markovchain a partir de las probabilidades de transición.

estados=c("vocal","consonante")
# matriz de transición idioma1
p1=matrix(c(0.51,0.49,0.9,0.1),byrow = TRUE,ncol=2,dimnames=list(estados,estados))
# proceso 1: idioma1
idioma1=new("markovchain",states=colnames(p1),byrow=TRUE,transitionMatrix=p1,name="idioma1")
# matriz de transición idioma2
p2=matrix(c(0.25,0.75,0.3,0.7),byrow = TRUE,ncol=2,dimnames=list(estados,estados))
# proceso 2: idioma2
idioma2=new("markovchain",states=colnames(p2),byrow=TRUE,transitionMatrix=p2,name="idioma2")

# y lo mostramos en formato data.frame
as(idioma1,"data.frame")

##           t0         t1 prob
## 1      vocal      vocal 0.51
## 2      vocal consonante 0.49
## 3 consonante      vocal 0.90
## 4 consonante consonante 0.10

as(idioma2,"data.frame")

##           t0         t1 prob
## 1      vocal      vocal 0.25
## 2      vocal consonante 0.75
## 3 consonante      vocal 0.30
## 4 consonante consonante 0.70

Verificamos que todos sus estados son recurrentes y la cadena es irreducible.

cat("Descripción idioma1\n")

## Descripción idioma1

summary(idioma1)

## idioma1  Markov chain that is composed by: 
## Closed classes: 
## vocal consonante 
## Recurrent classes: 
## {vocal,consonante}
## Transient classes: 
## NONE 
## The Markov chain is irreducible 
## The absorbing states are: NONE

cat("\n Descripción idioma2\n")

## 
##  Descripción idioma2

summary(idioma2)

## idioma2  Markov chain that is composed by: 
## Closed classes: 
## vocal consonante 
## Recurrent classes: 
## {vocal,consonante}
## Transient classes: 
## NONE 
## The Markov chain is irreducible 
## The absorbing states are: NONE

Planteamos ahora una serie de preguntas a responder.

1. En cada idioma, ¿cuál es la probabilidad de que si un texto empieza por vocal, el siguiente carácter sea consonante?

Calculamos pues, la distribución de los estados del sistema partiendo de una vocal, manualmente y con la función transitionProbability() o con conditionalDistribution(), que nos da la distribución condicional partiendo de un estado:

#determinamos el estado inicial
ini=c(1,0)
# y manualmente evaluamos los productos
final1=ini %*% p1; final1

##      vocal consonante
## [1,]  0.51       0.49

final2=ini %*% p2; final2

##      vocal consonante
## [1,]  0.25       0.75

# o extraemos la distribución condicional partiendo del estado inicial "vocal":
conditionalDistribution(idioma1,"vocal")

##      vocal consonante 
##       0.51       0.49

conditionalDistribution(idioma2,"vocal")

##      vocal consonante 
##       0.25       0.75

# o usamos la función de la librería markovchain
transitionProbability(idioma1,t0="vocal",t1="consonante")

## [1] 0.49

transitionProbability(idioma2,t0="vocal",t1="consonante")

## [1] 0.75

Resulta que en el idioma1 la probabilidad de que si un texto empieza por vocal el siguiente carácter sea consonante es de 0.49 y en el idioma2 de 0.75.

2. En cada idioma, ¿cuál es la probabilidad de que si un texto empieza por vocal, tras contar 10 caracteres más, encontremos una consonante?

Utilizamos el resultado que se mostró en la Ecuación (2.5) para calcular la matriz de transición de \(n\) pasos.

ini = c(1,0)
final1.10 = ini %*% ptran.n(p1,10); final1.10

##          vocal consonante
## [1,] 0.6475107  0.3524893

final2.10 = ini %*% ptran.n(p2,10); final2.10

##          vocal consonante
## [1,] 0.2857143  0.7142857

Si un texto empieza por voca, tras 10 caracteres encontraremos una consonante con probabilidad 0.35 en el idioma1 y con probabilidad 0.71 en el idioma2.

3. En cada idioma, en a palabra de 5 caracteres que empieza por vocal, ¿cuántas vocales esperamos encontrar? ¿Y si la palabra empieza por consonante?

Nos pregunta por el número de visitas o tiempo de ocupación de cada uno de los estados (vocal/consonante) cuando llegamos a 5 caracteres (en 4 transiciones entre caracteres). Calculamos pues la matriz de tiempos de ocupación hasta el instante \(n=4\) con la Ecuación (2.7), y para la que utilizamos la función mocupa.proceso() que definimos en la Sección Tiempos de ocupación.

n=4
mocupa1=mocupa.proceso(idioma1,n);mocupa1

##               vocal consonante
## vocal      3.493308   1.506692
## consonante 2.767393   2.232607

mocupa2=mocupa.proceso(idioma2,n);mocupa2

##               vocal consonante
## vocal      2.108844   2.891156
## consonante 1.156462   3.843537

Así, en el idioma1, si partimos de un texto que empieza en vocal, esperamos encontrar 3 vocales y si partimos de una consonante, 2.8 vocales. En el idioma2, si el primer carácter es vocal, encontraré 2.1 vocales y 3 vocales si el texto empieza por consonante.

4. ¿Cuántos caracteres habremos de leer por término medio en un texto (en cada idioma) hasta encontrar la primera vocal?

Nos están preguntando por el tiempo medio de primer paso por una vocal, partiendo de una consonante. Resolvemos con la función meanFirstPassageTime().

# todos los tiempos de primer paso
meanFirstPassageTime(idioma1)

##               vocal consonante
## vocal      0.000000   2.040816
## consonante 1.111111   0.000000

# tiempo de primer paso por una vocal
mfpt1=meanFirstPassageTime(idioma1,"vocal");mfpt1

## consonante 
##   1.111111

meanFirstPassageTime(idioma2)

##               vocal consonante
## vocal      0.000000   1.333333
## consonante 3.333333   0.000000

mfpt2=meanFirstPassageTime(idioma2,"vocal");mfpt2

## consonante 
##   3.333333

Tenemos así que el número medio de caracteres que esperamos encontrar en un texto hasta que aparezca por primera vez una vocal en el idioma 1 (partiendo de una consonante) es de 1, y en el idioma2 de 3.

5. En un texto que se inicia con una vocal, ¿con qué probabilidad encontraremos la primera consonante en los siguientes 3 caracteres? Compara los resultados para los dos idiomas.

Nos preguntan por la probabilidad de primer paso por el estado “consonante” partiendo de una “vocal” transcurridos tres caracteres. Utilizamos la función firstPassageMultiple() de la librería markovchain.

n=3
fpm1=firstPassageMultiple(idioma1,state="vocal",set=c("consonante"),n=n);fpm1

##        set
## 1 0.490000
## 2 0.249900
## 3 0.127449

fpm2=firstPassageMultiple(idioma2,state="vocal",set=c("consonante"),n=n);fpm2

##        set
## 1 0.750000
## 2 0.187500
## 3 0.046875

Así, tenemos que en el idioma1 la probabilidad de que la primera consonante que encontremos esté tres caracteres después de la vocal de inicio es de 0.127449, mientras que esta probabilidad en el idioma2 es sólo de 0.127449.

6. A partir de una consonante, ¿cuántos caracteres, por término medio, tardamos en encontrar otra consonante en cada idioma?

Nos están pidiendo el tiempo medio de recurrencia, esto es, volver a encontrar otra consonante si partimos de una consonante, que calculamos con la función meanRecurrenceTime().

mrt1=meanRecurrenceTime(idioma1);mrt1

##      vocal consonante 
##   1.544444   2.836735

mrt2=meanRecurrenceTime(idioma2);mrt2

##      vocal consonante 
##        3.5        1.4

Así, en el idioma1, desde la última consonante tendremos aproximadamente 3 caracteres hasta encontrar otra consonante, mientras que en el idioma2 sólo 1 por término medio.

7. ¿Qué proporción de vocales y consonantes hay en cada idioma? En un texto de 1000 caracteres que empieza por vocal, ¿cuántas vocales esperamos encontrar? ¿Y consonantes?

Para contestar la primera pregunta recurrimos a la distribución estacionaria, que nos da la probabilidad estacionaria para cada uno de los estados posibles, o lo que es lo mismo, la proporción de vocales y consonantes. Para responder la segunda pregunta, puesto que estamos en un texto muy largo con 1000 caracteres, ya no utilizaremos a la matriz de ocupación hasta un instante \(n=1000\), sino la distribución de ocupación, que coincide con la distribución estacionaria.

Sabemos que una CMTD irreducible y aperiódica tiene una única distribución estacionaria, que coincide con la distribución de ocupación. Que es irreducible ya lo comprobamos anteriormente al definir el sistema; verifiquemos pues que es aperiódica, esto es, que su periodo es 1, con la función period().

period(idioma1)

## [1] 1

period(idioma2)

## [1] 1

Así pues, calculamos la distribución estacionaria a continuación con la función steadyStates().

pi1=steadyStates(idioma1); pi1

##         vocal consonante
## [1,] 0.647482   0.352518

pi2=steadyStates(idioma2); pi2

##          vocal consonante
## [1,] 0.2857143  0.7142857

Tenemos que en el idioma1 el 65% de los caracteres en un texto son vocales, que predominan sobre las consonantes, mientras que en el idioma2 sólo un 29%, y la supremacía es de las consonantes, con un 71.4%.

Para calcular el número esperado de vocales y consonantes en un texto de 1000 caracteres, basta multiplicar estas probabilidades por 1000.

round(1000*pi1)

##      vocal consonante
## [1,]   647        353

round(1000*pi2)

##      vocal consonante
## [1,]   286        714

Así, en un texto de 1000 caracteres esperamos 647 vocales en el idioma1 y 286 en el idioma2.

Vamos a comprobar, además, que la distribución estacionaria verifica la ecuación de balance o del estado estacionario que se muestra en la Ecuación (2.10).

# ecuación de balance para la d.estacionaria del idioma1
pi1

##         vocal consonante
## [1,] 0.647482   0.352518

# es igual a su producto por la matriz de transición
pi1%*%p1

##         vocal consonante
## [1,] 0.647482   0.352518

# y sus probabilidades suman 1
sum(pi1)

## [1] 1

Con la distribución estacionaria comprobamos que se verifica la Ecuación (2.12) que nos permite calcular los tiempos medios de recurrencia con el inverso de las probabilidades estacionarias. Lo hacemos sólo con el idioma1.

1/pi1

##         vocal consonante
## [1,] 1.544444   2.836735

meanRecurrenceTime(idioma1)

##      vocal consonante 
##   1.544444   2.836735

8. Simula un texto de 1000 caracteres para el idioma1, empezando por una vocal y estima con esas simulaciones las probabilidades de transición. Compara los resultados con la matriz inicial.

Para simular una CMTD recurrimos a la función rmarkovchain().

set.seed(12)
n=1000
idioma1.sim=rmarkovchain(n,idioma1,t0="vocal",include.t0=TRUE)

Para estimar las probabilidades de transición con los textos simulados vamos a utilizar la librería markovchain que específicamente nos proporciona las frecuencias de salto, así como una estimación (junto con su error), basada en dichas frecuencias, bajo diversos procedimientos de estimación.

La función createSequenceMatrix() nos proporciona una matriz de frecuencias (absolutas o relativas) de las transiciones entre todos los estados posibles del sistema

# frecuencias de transiciones o saltos
createSequenceMatrix(idioma1.sim)

##            consonante vocal
## consonante         39   311
## vocal             311   339

# frecuencias relativas de transiciones o saltos
createSequenceMatrix(idioma1.sim,toRowProbs = TRUE )

##            consonante     vocal
## consonante  0.1114286 0.8885714
## vocal       0.4784615 0.5215385

Utilizamos ahora la función markovchainFit() que, a partir de datos simulados en estado estacionario, estima las probabilidades de transición. Podemos usar varios métodos de optimización alternativos, si bien por defecto se usa la estimación máximo-verosímil, method="mle". Las alternativas son EMV con suavizado de Laplace (“laplace”), bootstrap (“bootstrap”) y máximo a posteriori (“map”).

# Estimación de p1
p1.sim = markovchainFit(idioma1.sim,byrow=TRUE)
p1.sim;p1

## $estimate
## MLE Fit 
##  A  2 - dimensional discrete Markov Chain defined by the following states: 
##  consonante, vocal 
##  The transition matrix  (by rows)  is defined as follows: 
##            consonante     vocal
## consonante  0.1114286 0.8885714
## vocal       0.4784615 0.5215385
## 
## 
## $standardError
##            consonante      vocal
## consonante 0.01784285 0.05038626
## vocal      0.02713106 0.02832608
## 
## $confidenceLevel
## [1] 0.95
## 
## $lowerEndpointMatrix
##            consonante     vocal
## consonante 0.07645722 0.7898161
## vocal      0.42528562 0.4660204
## 
## $upperEndpointMatrix
##            consonante     vocal
## consonante  0.1463999 0.9873267
## vocal       0.5316375 0.5770566
## 
## $logLikelihood
## [1] -572.2645

##            vocal consonante
## vocal       0.51       0.49
## consonante  0.90       0.10

Esta función nos proporciona, además de la estimación de las probabilidades de transición, una estimación del error e intervalos de confianza.

estimate = as(p1.sim$estimate,"data.frame")
error = as.vector(p1.sim$standardError)
ic.low = as.vector(p1.sim$lowerEndpointMatrix)
ic.up = as.vector(p1.sim$upperEndpointMatrix)
cbind(estimate,error,ic.low,ic.up)

##           t0         t1      prob      error     ic.low     ic.up
## 1 consonante consonante 0.1114286 0.01784285 0.07645722 0.1463999
## 2 consonante      vocal 0.8885714 0.02713106 0.42528562 0.5316375
## 3      vocal consonante 0.4784615 0.05038626 0.78981615 0.9873267
## 4      vocal      vocal 0.5215385 0.02832608 0.46602035 0.5770566

9. Supón que accedes a un texto que transformas en una secuencia de vocales y consonantes (disponible para descarga en Github). Verifica, con dicha secuencia que proviene de una CMTD.

Para ello podemos utilizar la función verifyMarkovProperty() que resuelve un test de hipótesis basado en la Chi-cuadrado, sobre el cumplimiento de la propiedad de Markov con los datos proporcionados. Obtener un p-valor significativo significa que rechazaríamos esa propiedad y por lo tanto rechazaríamos que se trata de una CMTD.

# leemos los datos de Github
texto=read.csv("https://raw.githubusercontent.com/UMH1477/data/f4e4a62533e24a74be27b8984f9fc23eb1b1ff49/textos.csv")
# visualizamos el formato de los datos, con 2 columnas de texto
head(texto)

##       texto1     texto2
## 1      vocal consonante
## 2      vocal consonante
## 3 consonante consonante
## 4      vocal      vocal
## 5 consonante consonante
## 6 consonante consonante

# y ejecutamos el test sobre una de las columnas de texto
verifyMarkovProperty(texto$texto1)

## Testing markovianity property on given data sequence
## Chi - square statistic is: 2.056533 
## Degrees of freedom are: 5 
## And corresponding p-value is: 0.8412687

El p-valor es de 0.84, que no permite rechazar la propiedad de Markov.

Por último, para testar la estacionariedad, esto es, si \(p_{ij}(n)=p_{ij}\) para cualquier \(n\), tenemos la función assessStationarity(). Obtener un p-valor significativo significa que rechazaríamos esa propiedad y por lo tanto rechazaríamos que se trata de una CMTD.

assessStationarity(texto$texto1,5)

## Warning in assessStationarity(texto$texto1, 5): The accuracy of the statistical inference functions
## has been questioned. It will be thoroughly investigated in future versions of the package.

## Warning in chisq.test(mat): Chi-squared approximation may be incorrect

## Warning in chisq.test(mat): Chi-squared approximation may be incorrect

## The assessStationarity test statistic is:  0.0002538706 
## The Chi-Square d.f. are:  8 
## The p-value is:  1

10. Con los datos utilizados en el apartado anterior, verifica si alguno de los textos que se proporcionan en las columnas de la base de datos, se podría asimilar como perteneciente a alguno de los idiomas presentados, idioma1 o idioma2.

Para contrastar la similitud entre una secuencia y un proceso teórico que tenemos definido podemos utilizar la función verifyEmpiricalToTheoretical(). Veamos cómo funciona con los procesos idioma1 e idioma2.

# comparamos con el idioma1
verifyEmpiricalToTheoretical(texto$texto1,idioma1)

## Testing whether the
##            vocal consonante
## vocal      32800      31854
## consonante 31854       3491
## transition matrix is compatible with
##            vocal consonante
## vocal       0.51       0.49
## consonante  0.90       0.10
## [1] "theoretical transition matrix"
## ChiSq statistic is 2.460873 d.o.f are 2 corresponding p-value is 0.292165

## $statistic
##    vocal 
## 2.460873 
## 
## $dof
## [1] 2
## 
## $pvalue
##    vocal 
## 0.292165

El p-valor resultante es 0.29, con lo cual no se puede rechazar la hipótesis nula de que la secuencia dada es compatible con el idioma1. Podría ser pues, un texto de dicho idioma

Veamos ahora su compatibilidad con el idioma2:

# comparamos con el idioma2
verifyEmpiricalToTheoretical(texto$texto1,idioma2)

## Testing whether the
##            vocal consonante
## vocal      32800      31854
## consonante 31854       3491
## transition matrix is compatible with
##            vocal consonante
## vocal       0.25       0.75
## consonante  0.30       0.70
## [1] "theoretical transition matrix"
## ChiSq statistic is 76057.57 d.o.f are 2 corresponding p-value is 0

## $statistic
##    vocal 
## 76057.57 
## 
## $dof
## [1] 2
## 
## $pvalue
## vocal 
##     0

En este caso el p-valor es cero, por lo que rechazamos la compatibilidad y claramente aceptamos que este texto no proviene del idioma2.

2.7 Ejercicios

2.7.1 Básicos

Ejercicio B2.1. Para el proceso Meteorologia se desea conocer cuál es el tiempo estimado para tener un día lluvioso si hoy tenemos un día soleado.

Ejercicio B2.2. Para el proceso Mercado de valores se desea conocer cuál es el tiempo estimado en conseguir que las acciones alcancen los valores \(8, 9, 10\) partiendo de un valor inicial de \(5\).

Ejercicio B2.3. Consideramos el proceso Mercado de valores. Supongamos que el gerente financiero ha comprado 100 acciones a 5 dólares, y está interesado en conocer cuál es el beneficio neto esperado de su inversión en 5 días.

Ejercicio B2.4. En una boutique de café se cambian semanalmente los escaparates, promocionando tres tipos de café A, B y C en función de la demanda que registran. Según ello, la promoción de los tres tipos cambia de una semana a otra de acuerdo a la siguiente matriz de transición:

\[P = \begin{pmatrix} 0.3 & 0.3 & 0.4\\ 0.1 & 0.5 & 0.4\\ 0.3 & 0.2 & 0.5\\ \end{pmatrix}\]

Si en la semana 1 se expone el tipo A en el escaparate, ¿cuál es la probabilidad de que en la semana 10 se esté promocionando cualquiera de las tres marcas?

Ejercicio B2.5. Consideramos el proceso descrito en la sección Telecomunicaciones. Asumimos que en el estado inicial el buffer está lleno y deseamos conocer el número esperado de paquetes en el buffer en los instantes \(n =1, 2, 5\) y \(10\), asumiendo que el tamaño del buffer es 10 y que el número de paquetes que llegan en un instante es una variable aleatoria \(Bi(5, 0.2).\)

Ejercicio B2.6. Consideramos el proceso descrito en la sección Planificación de mano de obra. Supongamos que la empresa tiene 100 empleados en la semana 1, distribuidos como sigue: 50 en el nivel 1, 25 en el grado 2, 15 en el grado 3, y 10 en el grado 4. Si cada empleado tiene un comportamiento independiente respecto del resto ¿cuál es el número esperado de empleados en cada grado al principio de la semana 4?

Ejercicio B2.7. Consideramos el proceso descrito en la sección Problema de inventario. Estamos interesados en conocer cuál es la proporción de semanas en que el inventario estará lleno durante el proximo año, si empezamos con un inventario de 5 PCs?

Ejercicio B2.8. La secuencia de consonantes y vocales en el lenguaje humano se puede modelizar mediante una \(CMTD\) dado que después de una vocal siempre le sigue una consonante con probabilidad 0.49 y una vocal con probabilidad 0.51. Después de una consonante hay otra consonante con probabilidad 0.1. Codificamos un texto completo con una secuencia de ceros (vocal) y unos (consonantes). Obtén la matriz de transición para este proceso. Si el texto comienza con una consonante, ¿qué tipo de elemento será el que aparezca en la quinta posición de la secuencia? ¿Qué porcentaje de vocales y consonantes encontraremos en un texto de 2000 letras?

Ejercicio B2.9 Considera el proceso descrito en la sección Fiabilidad de máquinas, con dos máquinas. Supón que ambas máquinas están operativas al principio del día 0. Calcula la probabilidad de que el número de máquinas operativas al principio de los próximos tres días sea 2, 1 y 2, en ese orden.

Ejercicio B2.10. Calcula la matriz de ocupación \(M(10)\), la distribución límite y la estacionaria, para un proceso CMTD con matriz de transición dada por:

\[P=\begin{pmatrix} 0.1 & 0.3 & 0.2 & 0.4 \\ 0.1 & 0.3 & 0.4 & 0.2 \\ 0.3 & 0.1 & 0.1 & 0.5 \\ 0.15 & 0.25 & 0.35 & 0.25 \end{pmatrix}\]

2.7.2 Avanzados

Ejercicio A2.1. Los artículos llegan a un taller mecánico de forma determinista a un ritmo de uno por minuto. Cada artículo se comprueba antes de cargarlo en la máquina. Un artículo es adecuado con probabilidad \(p\) y defectuoso con una probabilidad \(1-p\). Si un artículo es defectuoso, se descarta; en caso contrario, se carga en la máquina. La máquina tarda exactamente 1 minuto en procesar el artículo, tras lo cual está lista para procesar el siguiente. Consideramos la variable aleatoria \(X_n\) que toma el valor \(0\) si la máquina está inactiva al principio del n-ésimo minuto y 1 si está iniciando el proceso.

1. Obtén la matriz de transición de este proceso.
2. Si \(p = 0.98\), ¿cuál es la proporción de tiempo en que la máquina está cargando un artículo durante las próximas ocho horas?
3. ¿Cuántas horas tendrán que pasar para que la máquina descarte un artículo cuando el primero no se descarta?

Supongamos ahora que la máquina puede procesar dos artículos simultáneamente. Sin embargo, tarda 2 minutos en completar el procesamiento. Delante de la máquina hay un contenedor en el que se pueden almacenar dos artículos no defectuosos. En cuanto hay dos artículos en la bandeja, se cargan en la máquina y ésta empieza a procesarlos.

4. Obtén la matriz de transición de este proceso.
5. ¿Cuál es la proporción de tiempo en que la máquina carga artículos durante las próximas ocho horas?
6. ¿Cuántas horas tendrán que pasar para que la máquina descarte dos artículos cuando los dos primeros no son defectuosos?

Ejercicio A2.2. Un vendedor vive en la ciudad “a” y es responsable de la venta de su producto en las ciudades “a,” “b” y ‘c.’ Cada semana tiene que visitar una ciudad diferente. Cuando está en su ciudad natal, le da igual la ciudad que visite a continuación, así que lanza una moneda y si sale cara va a “b” y si sale cruz va a “c.” Sin embargo, después de pasar una semana fuera de casa tiene una ligera preferencia por volver a casa, así que cuando está en las ciudades ‘b’ o ‘c’ lanza dos monedas. Si salen dos caras, se va a la otra ciudad; de lo contrario va a ‘a.’ Las sucesivas ciudades que visita forman una cadena de Markov con un espacio de estados \(S = \{a, b, c\}\) en la que la variable aleatoria \(X_n\) es igual a ‘a,’ ‘b’ o ‘c’ según su ubicación durante la semana \(n\). Obtén la matriz de transición de este proceso.

1. Empezando en su ciudad natal, ¿en qué ciudad se encontrará dentro de seis semanas?
2. ¿Cuál es la proporción de tiempo en que el vendedor se encontrará fuera de casa durante los próximos seis meses?
3. Si inicialmente está en la ciudad ‘a,’ ¿cuántas semanas tendrán que pasar para que visite la ciudad ‘c?’
4. Si el vendedor obtiene un beneficio de 1200 euros cuando pasa una semana en la ciudad ‘a,’ de 1200 euros cuando está en ‘b,’ y de 1250 cuando está en ‘c,’ ¿cuál será el beneficio esperado después de 12 semanas si comienza en su ciudad natal?
5. ¿Cuál será el beneficio esperado después de 12 semanas si desconocemos la ciudad de partida pero sabemos que hay una probabilidad de 0.5 que sea ‘a,’ 0.3 de que sea ‘b,’ y 0.2 de que sea ‘c?’

Ejercicio A2.3. Se lleva a cabo un análisis de mercado para conocer las preferencias de compras de coches en formato “renting,” según el cual cada año se renueva el coche a cada cliente del servicio en el mes de enero. La empresa está interesada en conocer si los clientes cambian el estilo de vehículo entre las tres opciones posibles (“sedan,” “station wagon,” y “convertible”) de un año al siguiente. Para estudiar este proceso se toman los datos de cambio de vehículo del último mes de enero:

Número ventas	Cambio
275	sedan for sedan
180	sedan for station wagon
45	sedan for convertible
80	station wagon for sedan
120	station wagon for station wagon
150	convertible for sedan
50	convertible for convertible

Este sistema se puede modelizar según una \(CMTD\) con espacio de estados \(S = \{s, w, c\}\).

1. Obtén la matriz de transición asociada a este proceso.
2. ¿Cuál es la probabilidad de que un cliente mantenga el mismo tipo de vehículo dentro de tres años? ¿y de cinco?
3. ¿Cuál es el tiempo esperado de permanencia con el mismo tipo de vehículo en los próximos 10 años?
4. ¿Cuál es el tiempo esperado hasta el primer cambio para cualquiera de los tipos considerados?
5. Si un “sedan” proporciona un beneficio anual de 1200 euros, el “station wagon” de 1500, y el “convertible” de 2500 euros, ¿cuál es el beneficio promedio esperado para un año? ¿y para 5 años?

Ejercicio A2.4. Un proceso de fabricación consiste en dos etapas consecutivas mediante el esquema siguiente:

• En la etapa 1, el 20% de las piezas son devueltas para su reelaboración, el 10% son desechadas, y el 70% restante pasan a la etapa 2.
• En la etapa 2, el 5% de las piezas deben ser devueltas a la etapa 1, el 10% deben ser reelaboradas, el 5% son desechadas, y el 80% restantes se consideran adecuadas para la venta.

1. Considerando todos los estados del proceso (e1 = etapa 1; e2 = etapa 2; d = desechado; v = venta) construye la matriz de transición correspondiente a este proceso.

La estructura de costes del proceso viene dada por:

• El coste del material que va a entrar entra en la etapa 1 es de 150 euros.
• Cada parte que es procesada en la etapa 1 incurre en un coste de 200 euros.
• Cada parte que es procesada en la etapa 2 incurre en un coste de 300 euros.
• Cada parte que no es rechazada en el etapa 1 pero si es rechazada en l etapa 2 incurre en un coste de 850 euros.
• El material que es desechado debe someterse a un proceso de eliminación especial con u coste de 50 euros por parte.

El sistema es capaz de tratar suficiente material para generar 100 partes al cabo de un día (aptas para la venta o desechadas).

2. Plantea un algoritmo de simulación que permita responder a cuál es el coste medio del proceso de fabricación para los próximos 15 días. ¿Y la variabilidad estimada de dicho coste?
3. Si la empresa quiere asegurar un beneficio neto del 5%, ¿a qué precio debe vender las piezas aptas para asegurar dicho beneficio de acuerdo al coste medio estimado del proceso? ¿Cuál sería el rango de venta teniendo en cuenta las fluctuaciones del coste medio?

Ejercicio A2.4 simplificado Un proceso de fabricación consiste en dos etapas consecutivas mediante el esquema siguiente:

• En la etapa 1, el 20% de las piezas son devueltas para su reelaboración, el 10% son desechadas, y el 70% restante pasan a la etapa 2.
• En la etapa 2, el 5% de las piezas deben ser devueltas a la etapa 1, el 10% deben ser reelaboradas, el 5% son desechadas, y el 80% restantes se consideran adecuadas para la venta.
• Las piezas desechadas se quedan desechadas y las que se ponen a la venta se quedan en el mercado.

1. Considerando todos los estados del proceso (e1 = etapa 1; e2 = etapa 2; d = desechado; v = venta) construye la matriz de transición correspondiente a este proceso.

La estructura de costes del proceso viene dada por:

• Cada paso por la etapa 1 es de 150 euros.
• Cada paso por la etapa 2 es de 300 euros.
• Cada producto desechado debe someterse a un proceso de eliminación especial con un coste de 50 euros por parte.
• Poner a la venta un producto conlleva unos costos de distribución de 10 euros.

El sistema es capaz de tratar suficiente material para generar 100 partes al cabo de un día (aptas para la venta o desechadas).

2. Plantea un algoritmo de simulación que permita reproducir el recorrido de un producto en la cadena de producción, iniciándose en la etapa 1. Evalúa el coste de ese producto.

3. Simula el proceso de producción durante 10 días y con todos los productos procesados da una estimación del coste medio de producción. Calcula el error y un intervalo de confianza. Interpreta el intervalo de confianza.

4. Si la empresa quiere asegurar (con garantías del 95%) un beneficio neto del 5%, ¿a qué precio debe vender cada producto?

Ejercicio A2.5. Se lanza un misil al que se le envía una secuencia de señales de corrección de rumbo cuando es necesario. Supongamos que el sistema tiene cuatro estados que se etiquetan como sigue:

• Estado 0: en rumbo, sin necesidad de correcciones.
• Estado 1: correcciones mínimas.
• Estado 2: correcciones mayores.
• Estado 3: desviación no controlable que hace necesaria la autodestrucción del mísil.

Sea \(X_n\) que representa el estado del sistema después de la n-ésima corrección, de forma que si el mísil está en curso en el instante \(n\) se mantendrá en curso durante todo el vuelo; si necesita una corrección mímima, entonces con probabilidad 0.5 no será necesaria ninguna corrección posterior, con probabilidad 0.25 será necesaria una nueva corrección menor, y con probabilidad 0.25 será necesaria una corrección mayor. Si en el instante \(n\) necesitamos una corrección mayor, con probabilidad 0.5 necesitaremos una corrección menor a continuación, con probabilidad 0.25 necesitaremos otra corrección mayor, y con probabilidad 0.25 deberemos abortar la misión.

1. ¿Cuál es la matriz de transición para este proceso?
2. Si un mísil necesita una corrección menor al inicio del lanzamiento, ¿cuál será su situación después de 3 correcciones?

El mísil gasta 50000 libras de combustible en el lanzamiento, 1000 libras cuando una corrección menor es necesaria, y 5000 cuando una corrección mayor es necesaria. Simula el proceso para tratar de responder a estas preguntas:

3. ¿Cuál será el consumo medio de combustible después de 4 correcciones?
4. ¿Y si lanzamos 6 cohetes a la vez?

Ejercicio A2.6. Al comienzo de cada semana, el estado de una máquina se determina midiendo la cantidad de corriente eléctrica que utiliza. En función de su lectura de amperaje, la máquina se clasifica en uno de los cuatro estados siguientes: bajo, medio, alto, fallido. Una máquina en estado bajo tiene una probabilidad de 0.05, 0.03 y 0.02 de estar en el estado medio, alto o fallido, respectivamente, al comienzo de la siguiente semana. Una máquina en estado medio tiene una probabilidad de 0.09 y 0.06 de estar en estado alta o fallida, respectivamente, al inicio de la siguiente semana; no puede, por sí sola, pasar al estado bajo. Una máquina en estado alto tiene una probabilidad de 0.1 de estar en el estado fallido al comienzo de la siguiente semana; no puede, por sí misma, pasar al estado bajo o medio. Si una máquina se encuentra en estado de fallo al comienzo de la semana, se inicia inmediatamente la reparación de la máquina para que (con probabilidad 1) esté en el estado bajo al comienzo de la semana siguiente.

1. Modeliza este proceso como una \(CMTD\) y obtén la correspondiente matriz de transición.
2. Si una máquina nueva siempre comienza en el estado bajo, ¿cuál es la probabilidad de que la máquina esté en estado de fallo tras tres semanas?
3. ¿Cuál es la probabilidad de que una máquina nueva tenga al menos un fallo dentro de tres semanas?
4. En promedio, ¿cuántas semanas al año estará trabajando la máquina?

Cada semana que la máquina está en estado bajo, se obtiene un beneficio de 1.000 dólares; cada semana que la máquina está en el estado medio, se obtiene un beneficio de 500 dólares; cada semana que la máquina está en estado alto, se obtiene un beneficio de 400 dólares; y la semana en la que se fija un fallo, se incurre en un coste de 700 dólares.

5. ¿Cuál es el beneficio semanal a medio a largo plazo obtenido por la máquina?

Se ha sugerido cambiar la política de mantenimiento de la máquina. Si al comienzo de una semana la máquina está en el estado alto, la máquina se deja fuera de servicio y es reparada para que al inicio de la siguiente semana vuelva a estar en el estado bajo. Cuando se realiza una reparación se incurre en un coste de 600 euros.

6. ¿Merece la pena esta nueva política de mantenimiento?

Ejercicio A2.7. Nos interesa el traslado de planta de los pacientes dentro de un hospital. A efectos de nuestro análisis, consideraremos que el hospital tiene tres tipos diferentes de plantas: habitaciones de “cuidados generales,” habitaciones de “cuidados especiales” y “cuidados intensivos.” Basándonos en datos anteriores, el 60% de los pacientes que llegan, ingresan inicialmente en la categoría de “cuidados generales,” el 30% en la de “cuidados especiales” y el 10% en la de “cuidados intensivos.” Un paciente de “cuidados generales” tiene un 55% de posibilidades de ser dado de alta sano al día siguiente, un 30% de permanecer en la planta de “cuidados generales,” y un 15% de ser trasladado a la planta de “cuidados especiales.” Un paciente de “cuidados especiales” tiene un 10% de posibilidades de ser dado de alta al día siguiente, un 20% de ser trasladado a “cuidados generales,” un 15% de pasar a “cuidados intensivos.” Un paciente de “cuidados intensivos” nunca es dado de alta, hasta que muestra mejoría. Las probabilidades de que el paciente sea trasladado a “cuidados generales,” “cuidados especiales” o que permanezca en “cuidados intensivos” son del 5%, el 30% o el 55%, respectivamente.

1. Modeliza este sistema como una \(CMTD\) y obtén la correspondiente matriz de transición.
2. ¿Cuál es la probabilidad de que un paciente ingresado en la sala de cuidados intensivos salga sano del hospital?
3. ¿Cuál es el número esperado de días que un paciente, ingresado en cuidados intensivos pasará en la UCI?
4. ¿Cuál es la duración prevista de la estancia de un paciente ingresado en el hospital como paciente de cuidados generales?
5. Durante un día normal, ingresan en el hospital 100 pacientes. ¿Cuál es el número medio de pacientes en la UCI?

Ejercicio A2.8. La fabricación de un determinado tipo de placa electrónica consta de cuatro pasos: preparación, montaje, inserción y soldadura. Después de la etapa de montaje, el 5% de las piezas deben ser retiradas; después de la etapa de inserción, el 20% de las piezas son retiradas; y después de la etapa de soldadura, el 30% de las piezas deben ser devueltas a la inserción y el 10% debe desecharse. Suponemos que cuando una pieza se devuelve a una etapa de procesamiento, es tratada como cualquier otra pieza que entra en esa etapa.

1. Modeliza este sistema como una \(CMTD\) y obtén la correspondiente matriz de transición.
2. Si un lote de 100 placas comienza este proceso de fabricación, ¿cuántas se espera que acaben desechadas?
3. ¿Con cuántas placas deberíamos empezar si el objetivo es que el número esperado de placas que terminen siendo aceptadas sea igual a 100?
4. ¿Con cuántas placas deberíamos empezar si queremos estar seguros al 90% de que terminamos con un lote de 100 placas?

Cada vez que una placa pasa por una etapa de procesamiento, los costes directos de mano de obra y material son de 10 euros para la preparación, 15 euros para el montaje, 25 euros para la inserción y 20 euros para la soldadura. La materia prima cuesta 8 euros, y una placa desechada devuelve 2 euros. La tasa media de gastos generales es de 1.000.000 de euros al año, lo que incluye valores de recuperación de capital. El ritmo de procesamiento medio es de 5.000 placas por semana.

5. Queremos fijar un precio por placa para que los ingresos previstos sean un 25% superiores a los costes previstos. ¿En qué valor debemos fijar el precio?

Ejercicio A2.9. Dentro de un área de mercado determinada hay dos marcas de jabón que la mayoría de la gente utiliza, el “superjabón” y el “jabón barato,” y el mercado actual se divide por igual entre las dos marcas. Una empresa está pensando en introducir una tercera marca llamada “jabón extra limpio,” y ha realizado algunos estudios iniciales sobre las condiciones del mercado. Sus estimaciones de las pautas de compra semanales son las siguientes: si un cliente compra superjabón esta semana, hay un 75% de posibilidades de que la próxima semana vuelva a comprarlo, un 10% de probabilidad de que use el jabón extra limpio y un 15% de probabilidad de que use el jabón barato. Si un cliente compra el jabón extra limpio esta semana, hay un 50% de probabilidades de que cambie, y si lo hace, siempre será al superjabón. Si un cliente compra jabón barato esta semana, es igual de probable que la próxima semana el cliente compre cualquiera de las tres marcas.

1. Asumiendo que se cumplen las condiciones de Markov, ¿cuál es la mariz de transición para este proceso?
2. ¿Cuál es la cuota de mercado a largo plazo del nuevo jabón?
3. ¿Cuál será la cuota de mercado del nuevo jabón dos semanas después de su introducción?

El mercado consta de aproximadamente un millón de clientes cada semana. Cada compra de superjabón produce un beneficio de 15 céntimos; una compra de jabón barato produce un beneficio de 10 céntimos; y una compra del extra limpio produce un beneficio de 25 céntimos. Supongamos que el mercado se encuentra en estado estacionario con la misma distribución entre los dos productos ya comercializados. La campaña publicitaria inicial para introducir la nueva marca fue de 100.000 dólares.

4. ¿Cuántas semanas pasarán hasta que se recuperen los 100.000 dólares de los ingresos añadidos del nuevo producto?
5. La empresa considera que con estas tres marcas, una campaña publicitaria de 30.000 dólares por semana aumentará el mercado total semanal en un cuarto de millón de clientes? ¿Merece la pena la campaña? (Utiliza un criterio de media a largo plazo).

Ejercicio A2.10. Considera una \(CMTD\) con espacio de estados \(S=\{a, b, c\}\) y con matriz de transición:

\[P = \begin{pmatrix} 0.3 & 0.5 & 0.2\\ 0.1 & 0.2 & 0.7\\ 0.8 & 0.0 & 0.2\\ \end{pmatrix}\]

Cada visita al ‘estado a’ produce un beneficio de 5 dólares, cada visita al ‘estado b’ produce un beneficio de 10 dólares, y cada visita al ‘estado c’ produce un beneficio de 12 dólares.

1. Escribir un algoritmo que simule la cadena de Markov para poder estimar el beneficio esperado por paso, asumiendo que la cadena siempre comienza en el ‘estado a.’
2. Realizar 10 repeticiones del proceso con 25 pasos en cada una y obtener el valor medio del beneficio y rango para las 10 réplicas.
3. Realizar 10 repeticiones con 1000 pasos en cada una y obtener el valor medio del beneficio y rango para las 10 réplicas.
4. Comparar las estimaciones y los rangos de los dos escenarios propuestos.