Unidad 5 Sistemas de colas

En esta unidad, consideramos específicamente los sistemas basados en colas de espera. Nos centraremos en los más sencillos y que están basados en el Proceso de Poisson, algunos de los cuales ya hemos presentado en la unidad anterior.

Los sistemas de colas son muy habituales en nuestra vida y es interesante dedicar tiempo de estudio para poder responder a preguntas como:

¿Cuántos clientes hay en la cola?
¿Cuánto tiempo esperan los clientes?
¿Cuántos clientes se pierden por la ineficiencia del sistema?
¿Cómo están de ocupados los servidores?

Comenzamos introduciendo la nomenclatura estándar para los sistemas de colas:

Proceso de llegadas: Es la forma en que los “clientes” entran al sistema, y se refieren a los tiempos entre llegadas sucesivas, que se modelizan como variables aleatorias iid. El proceso de llegadas se describe con la distribución de los tiempos entre llegadas, representada por los símbolos: $M$ (exponencial), $G$ (general), $D$ (determinista), y $E_k$ (Erlang con $k$ fases).
Tiempos de servicio: Se asume que los tiempos de servicio de los sucesivos clientes que llegan al sistema son variables aleatorias iid. Se representan con las mismas letras que los tiempos entre llegadas.
Numero de servidores: Habitualmente se denota por $s$ y se asume que todos los servidores que dan servicio a los clientes en el sistema se comportan de la misma forma; además, se asume que cada cliente (o lote de clientes en las colas por lotes) es atendido por un único servidor.
Capacidad del sistema: Habitualmemte se denota por $K$ y es la capacidad total del sistema, esto es, el número de clientes que pueden ser atendidos más los que pueden esperar en la cola. Si un nuevo cliente encuentra $K$ clientes en el sistema, este se pierde. La capacidad del sistema puede ser finita o infinita, pero si no se indica nada, se considera infinita.
Disciplina de la cola: Se refiere a cómo son tratados los nuevos clientes cuando acceden al sistema. Las opciones habituales son: FIFO (el primero que entra es el primero en ser atendido), LIFO (el último en llegar es el primero en ser atendido), SIRO (servicio en orden aleatorio), y PRI (cola con prioridades). Si no se indica nada, se asume por defecto la disciplina FIFO.

La notación habitual de una cola se establece como:

\[\text{Llegadas} / \text{Servicio} / \text{Servidores} / \text{Capacidad} / \text{Disciplina}\]

Una cola $M/M/1$ representa que tanto el proceso de llegadas como de servicio responde a una distribución exponencial, sólo disponemos de un servidor, la capacidad de la cola es infinita y la disciplina de servicio es FIFO.

Todas las colas que presentamos en esta unidad pueden ser descritas mediante procesos de nacimiento y muerte, tal y como los definimos en la unidad anterior. Sin embargo, en el punto siguiente introducimos la terminología básica de los sistemas de colas.

5.1 Terminología y medidas de eficiencia

Notación habitual de los sistemas de colas:

$N(t)$: Denota el número de clientes en el sistema en el instante $t$. $N(t)$ es una CMTC con espacio de estados discreto.
$N_q(t)$: Representa el número de clientes en la cola en el instante $t$.
$P_n(t)$: Es la probabilidad de que en el instante $t$ se encuentren $n$ clientes en el sistema. A estos efectos se supone conocido el número de clientes en el instante cero (usualmente dicho número es cero). Estas probabilidades se corresponden con las probabilidades de transición comenzando en el estado 0, que vimos en la unidad anterior.
$s$: Denota el número de servidores del mecanismo de servicio.
$\lambda_n$: Representa el número medio de llegadas de clientes al sistema, por unidad de tiempo, cuando ya hay $n$ clientes en él. También se denomina tasa de llegadas (o nacimientos en terminología de procesos de nacimiento-muerte). Cuando las tasas de llegada no dependen de $n$ (es decir, la tasa de llegadas no depende del número de clientes en el sistema, y es constante) $\lambda_n$ se denota por $\lambda$.
$\mu_n$: Es el número medio de clientes que completan el servicio por unidad de tiempo, cuando hay $n$ clientes en el sistema. Es frecuente referirse a los $mu_n$ como tasas de compleción de servicio (o simplemente tasas de servicio; tasas de muerte en procesos nacimiento-muerte). Si los servidores son siempre regulares en el servicio que prestan (siempre lo realizan al mismo ritmo), y $\mu$ es el número medio de clientes que puede atender cada servidor por unidad de tiempo, entonces $\mu_n = n\mu$ cuando hay $n$ clientes en el sistema ($n = 1, 2,... ,s$) y $\mu_n = s\mu$ cuando hay más clientes que servidores ($n > s$).
$\rho$: Es la llamada razón o constante de utilización del sistema, y también intensidad de tráfico. Se define, como el cociente entre la tasa de llegadas y la tasa máxima de servicio con los servidores disponibles.

\[\rho = \frac{\lambda}{s\mu}\]

Cuando los $\lambda_n$ son constantes y todos los servidores tienen la misma distribución de tiempo de servicio, $\lambda$ es el número medio de clientes que entran en el sistema y $s\mu$ es el número máximo de clientes a los que pueden dar servicio los $s$ servidores por unidad de tiempo. En estas condiciones, $\rho$ representa la fracción de recursos del sistema que es consumida por los clientes. Así, intuitivamente, parece necesario que se cumpla $\rho < 1$ para garantizar que el sistema es capaz de dar servicio a todos los clientes que llegan. Cuanto más cercano a 1 está $\rho$, más tráfico ha de soportar el sistema, y en consecuencia menos tiempo libre tendrán los servidores, o más espera habrán de soportar los clientes.

En toda la unidad asumimos que todos los modelos de colas con los que trabajamos son estacionarios, de forma que los procesos $\{N(t), t \geq 0\}$ y {N_q(t), t }$ no cambian con el tiempo. Podemos entonces definir las variables de interés del sistema:

$N$: Es la variable aleatoria que contabiliza el número de clientes en el sistema.
$N_q$: Denota la variable aleatoria número de clientes en la cola.
$p_n$: Probabilidad de que se encuentren $n$ clientes en el sistema $(n = 0, 1,... )$.

Asociado a todo sistema de colas, definiremos ciertas medidas de eficiencia que permitirán estudiar su comportamiento:

$L$: Representa el número medio de clientes en el sistema, es decir $L = E(N)$.
$L_q$: Es el número medio de clientes en la cola, o lo que es lo mismo, el tamaño esperado de la cola, $L_q = E(N_q)$.
$T$: Es la variable aleatoria que describe el tiempo que un cliente pasa en el sistema (siendo atendido y en espera a ser atendido).
$W$ : Es el tiempo medio que un cliente está en el sistema, o simplemente, $W = E(T)$.
$T_q$: Representa el tiempo que un cliente espera en la cola.
$W_q$: Denota el tiempo medio de espera en la cola de un cliente genérico, $W_q = E(T_q)$.

5.2 Formulas de Little

En los modelos con distribución del tiempo entre llegadas y distribución del servicio exponencial (así como en muchos otros modelos más generales llamados ergódicos) se verifican ciertas fórmulas que relacionan los números medios de clientes, en el sistema o en la cola, con los tiempos medios de un clientes en el sistema o en la cola. Estas son las llamadas fórmulas de Little.

Cuando las tasas de llegada son constantes (es decir $\lambda_n = \lambda$ para $n \in S$), la primera fórmula de Little establece que el número medio de clientes en el sistema es igual a la tasa de llegadas multiplicada por el tiempo medio de permanencia en el sistema:

\[L = \lambda W,\] mientras que la segunda viene a ser un equivalente de la anterior, referido a la cola: el tiempo medio de permanencia en cola es igual a la tasa de llegadas por el tiempo medio de espera en cola:

\[L_q = \lambda W_q.\] Estas fórmulas las podemos entender intuitivamente razonando con los costes y ganancias esperadas en el sistema. Para estimar los costes, supongamos que por cada instante de tiempo que permanezca en el sistema, cada cliente ha de pagar 1€. Si cada uno de ellos permanece en media $W$ unidades de tiempo y llegan $\lambda$ clientes por unidad de tiempo, los pagos que se realizarán en total por unidad de tiempo será de $\lambda W$. Por otro lado, atendiendo al número medio de clientes que hay en el sistema en un instante cualquiera, $L$, la ganancia total que se recibirá si cada uno paga 1€ por unidad de tiempo será de $1 \cdot L=L$. Puesto que las ganancias del sistema provienen exclusivamente de los pagos que se realizan, tenemos la igualdad $L=\lambda W$. Un razonamiento análogo es válido para la segunda fórmula de Little.

Obviamente, las fórmulas de Little no pueden ser válidas si las $\lambda_n$ no son constantes pero sí pueden generalizarse a esa situación mediante:

\[L = \bar{\lambda}W\] \[L_q = \bar{\lambda}W_q\]

con

\[\bar{\lambda} = \sum_{n = 0}^{\infty} \lambda_np_n.\] Otra relación importante (en este caso para relacionar $W$ y $W_q$) es la dada por:

\[W = W_q + \frac{1}{\mu}\] Su deducción es inmediata pues viene a decir que el tiempo medio que un cliente permanece en el sistema, $W$, coincide con la suma del tiempo medio en la cola, $W_q$, y el tiempo medio que tarda en ser atendido, $1/\mu$$.

Una derivación de las fórmulas de Little permite estimar el número esperado de clientes que están siendo atendidos, o lo que es lo mismo, servidores que están trabajando -denotado por $B$-, como el ratio de la tasa de llegadas y la tasa de servicios, \[B=\lambda/\mu.\]

5.3 Colas con un único servidor

En este apartado presentamos los aspectos más relvantes referidos a los sistemas de colas con un único servidor. empezando por el más sencillo que considera tiempos de llegadas y servicio exponenciales, y con un único servidor.

Definición 5.1 Una cola M/M/1 es estable si $\sum_{i \in S}p_j=1$, e inestable cuando dicha suma es menor que 1, siendo $p_j=lim_{t\rightarrow \infty} Pr[N(t)=j], j\geq 0$ la probabilidad a largo plazo de que haya $j$ clientes en el sistema.

5.3.1 M/M/1

Comenzamos con el sistema más sencillo, donde se consideran tiempos de llegadas y servicio exponenciales, un único servidor, capacidad del sistema infinita y prioridad0 + FIFO. De esta forma, tanto las tasas de llegadas como las tasas de servicio son constantes:

\[ \begin{matrix} \lambda_n = \lambda & n = 0, 1,...\\ \mu_n = \mu & n = 1, 2,... \end{matrix}\]

y la matriz de tasas es:

\[ R = \begin{pmatrix} 0 & \lambda & 0 & 0 & ...\\ \mu & 0 & \lambda & 0 & ...\\ 0 & \mu & 0 & \lambda & ...\\ \vdots & \vdots & \vdots & \vdots & \vdots \end{pmatrix}\]

Teorema 5.1 Definamos \[c_n=\frac{\lambda_{n-1}\lambda_n ...\lambda_1 \lambda_0}{\mu_n \mu_{n-1} ...\mu_2 \mu_1}=\rho^n, \qquad n=1,2,...\]

Una cola de nacimiento y muerte con capacidad infinita es estable si y sólo si \[\sum_{j=0}^\infty c_j < \infty.\] Cuando la cola es estable, su distribución límite viene dada por \[\begin{equation} p_i=\frac{c_i}{\sum_{j=0}^{\infty} c_j}, \quad i \geq0 \end{equation}\]

Como resultado del teorema anterior, una cola M/M/1 es estable si y sólo si $\rho<1$. Derivemos este resultado aplicando dicho teorema. Como en este caso las tasas de llegadas y servicios son constantes, tenemos que \[c_n=\frac{\lambda^n}{\mu^n}=\rho^n.\] La condición $\sum_{j=0}^\infty c_j < \infty$ es pues equivalente a $\sum_{j=0}^\infty \rho^j < \infty$, y esta serie infinita toma un valor finito sólo cuando $\rho<1$, es decir, si el número medio de clientes que entran en el sistema por unidad de tiempo es menor que el número medio de clientes que pueden ser atendidos por servidor por unidad de tiempo: \[\sum_{j=0}^\infty \rho^j=\begin{cases} \frac{1}{1-\rho}, \ \rho<1 \\ \infty, \quad \rho \geq 1 \end{cases} \] Por lo tanto, cuando $\rho<1$ la cola es estable y la distribución estacionaria viene dada por \[\begin{equation} p_i=\frac{\rho^i}{\sum_{j=0}^{\infty} \rho^j}=\rho^i (1-\rho), \quad i\geq 0. \tag{5.1} \end{equation}\]

Esta distribución (5.1) para el número de clientes en el sistema se corresponde con una distribuión geométrica de parámetro $(1 - \rho)$. Por tanto, el número medio de clientes en el sistema, $L$, viene dado por:

\[L = E(N) = \sum_{n = 0}^{\infty} np_n = \sum_{n = 0}^{\infty} n (1-\rho) \rho^n=\frac{\rho}{1-\rho} = \frac{\lambda}{\mu - \lambda}.\]

Teorema 5.2 El número esperado de clientes en cualquier sistema de colas viene dado por

\[L_q = L - (1 - p_0).\]

Este resultado aplicado a la cola M/M/1 da que el número esperado de clientes en la cola será \[L_q = \frac{\rho}{1-\rho}-(1-\rho)=\frac{\lambda^2}{\mu(\mu-\lambda)}\]

Aplicando las fórmulas de Little obtenemos el tiempo medio que un cliente está en el sistema, $W$, y también el tiempo esperado en cola, $W_q$:

\[\begin{eqnarray*} W &=& \frac{L}{\lambda} = \frac{1}{\mu - \lambda},\\ W_q &=& \frac{L_q}{\lambda} = \frac{\lambda}{\mu(\mu - \lambda),} \end{eqnarray*}\]

de donde derivamos que:

\[W = W_q + \frac{1}{\mu}.\]

Si se desea tener más información sobre la espera de clientes en la cola o en el sistema, debe calcularse la distribución de probabilidad de las variables $T$ y $T_q$. Estas distribuciones permitirán calcular la probabilidad de cualquier suceso relativo al tiempo de estancia en la cola o en el sistema. Si denotamos por $W(t)$ y $W_q(t)$ a las correspondientes funciones de distribución de $T$ y $T_q$ tendremos:

\[W(t) = 1 - exp[-(\mu - \lambda)t]\]

\[ W_q(t) = \begin{cases} 1 - \frac{\lambda}{\mu}exp[-(\mu - \lambda)t] & \text{ si } t \geq 0\\ 0 & \text{ si } t < 0 \end{cases} \]

Ejemplo 5.1 Operador de elevador. Un operador de un pequeño elevador de grano tiene un único muelle de descarga. Las llegadas de camiones durante la temporada alta forman un proceso de Poisson con una tasa de llegada media de cuatro por hora. Debido a la variación de las cargas (y al deseo de los conductores de hablar) el tiempo que cada camión pasa frente al muelle de descarga se aproxima por una variable aleatoria exponencial con una media de 14 minutos. Suponiendo que que las plazas de aparcamiento son ilimitadas, el sistema de colas $M/M/1$ puede describir el comportamiento del proceso con tasas de llegadas $= 4 $ y tasa de servicio $\mu = 60/14$ (tiempos expresados en horas).

¿Cuál es la probabilidad de que el muelle de descarga esté inactivo?
¿Cuál es la probabilidad de que haya exactamente tres camiones esperando?
¿Cuál es la probabilidad de que haya cuatro o más camiones en el sistema?

Resolvemos el ejemplo de dos formas diferentes: a) teóricamente con las fórmulas anteriores, b) con la libreria queueing.

Al final de la unidad presentamos la solución de simmer para simular de una cola $M/M/1$. En este último caso deberemos aproximar las cantidades de interés mediante los correspondientes estimadores Monte-Carlo, si repetimos la simulación del sistema un número adecuado de veces.

Para responder a la primera pregunta tenemos en cuenta que $\rho = 0.9333$ y que la probabilidad buscada es la que corresponde al estado $0$ de la distribución estacionaria, es decir,

\[p_0 = 1 - \rho\]

lambda=4
mu=60/14
rho=lambda/mu
p0=1-rho
cat("\n p0=",round(p0,4))

## 
##  p0= 0.0667

En cuanto a la segunda pregunta debemos tener en cuenta que:

\[P(N_q = 3) = P(N = 4) = p_4\]

p4= (1-rho)*rho^4 
cat("P(Nq = 3)=",round(p4,4))

## P(Nq = 3)= 0.0506

Para resolver la última pregunta tenemos que:

\[P(N \geq 4) = 1 - P(N \leq 3) = 1 - \sum_{n = 0}^{3} p_n = \rho^4 \]

p=rho^4 
cat("P(N>=4)=",round(p,4))

## P(N>=4)= 0.7588

Utilizamos ahora la librería queueing para resolver las mismas preguntas. En primer lugar tenemos que definir el sistema y sus características (tasas de llegada, tasas de servicio, y número de elementos de la distribución estacionaria que debemos calcular). Para ello utilizamos la función NewInput() con $n = 4$ elementos de la distribución estacionaria, ya que las probabilidades buscadas hacen referencia a esos cuatro primeros valores.

library(queueing)
# Definición del entorno
env.MM1 <- NewInput.MM1(lambda = 4, mu = 60/14, n = 4)
# Características del sistema
s.MM1 <- QueueingModel(env.MM1)

Los valores y funciones del sistema que proporciona la función son:

$RO$ = valor de intensidad de tráfico $\rho$.
$Lq$ = número medio de clientes en la cola.
$VNq$ = varianza del número de clientes en la cola.
$Wq$ = tiempo medio de espera en la cola.
$VTq$ = varianza del tiempo de espera en la cola.
$L$ = número medio de clientes en el sistema.
$VN$ = varianza del número de clientes en el sistema.
$W$ = tiempo medio que un cliente está en el sistema.
$VT$ = varianza del tiempo que un cliente está en el sistema.
$Wqq$ = tiempo medio que un cliente permanece en la cola cuando esta existe.
$Lqq$ = número medio de clientes en la cola cuando esta existe.
$Pn$ = Distribución estacionaria del sistema.
$Qn$ = Probabilidad de que un nuevo cliente encuentre $n$ clientes.
$FW$ = Función de distribución de $W$ para un conjunto de valores de $t$.
$FWq$ = Función de distribución de $W_q$ para un conjunto de valores de $t$.

Veamos la salida completa:

# Medidas del sistema
s.MM1

## $Inputs
## $lambda
## [1] 4
## 
## $mu
## [1] 4.285714
## 
## $n
## [1] 4
## 
## attr(,"class")
## [1] "i_MM1"
## 
## $RO
## [1] 0.9333333
## 
## $Lq
## [1] 13.06667
## 
## $VNq
## [1] 208.1956
## 
## $Wq
## [1] 3.266667
## 
## $VTq
## [1] 12.19556
## 
## $Throughput
## [1] 4
## 
## $L
## [1] 14
## 
## $VN
## [1] 210
## 
## $W
## [1] 3.5
## 
## $VT
## [1] 12.25
## 
## $Wqq
## [1] 3.5
## 
## $Lqq
## [1] 15
## 
## $Pn
## [1] 0.06666667 0.06222222 0.05807407 0.05420247 0.05058897
## 
## $Qn
## [1] 0.06666667 0.06222222 0.05807407 0.05420247 0.05058897
## 
## $FW
## function (t) 
## {
##     1 - exp(-t/W)
## }
## <bytecode: 0x7f91ba932c18>
## <environment: 0x7f91ba932550>
## 
## $FWq
## function (t) 
## {
##     1 - (RO * exp(-t/W))
## }
## <bytecode: 0x7f91ba933078>
## <environment: 0x7f91ba932550>
## 
## attr(,"class")
## [1] "o_MM1"

Podemos responder ahora a las cuestiones de interés sin más que buscar en los elementos que proporciona la función.

# ¿cuál es la probabilidad de que el muelle de descarga esté inactivo?
s.MM1$Pn[1]

## [1] 0.06666667

# ¿cuál es la probabilidad de que haya exactamente tres camiones esperando?
# se corresponde con el elmento 4 + 1 de pn
s.MM1$Pn[5]

## [1] 0.05058897

# ¿cuál es la probabilidad de que haya cuatro o más camiones en el sistema?
1- sum(s.MM1$Pn[1:4])

## [1] 0.7588346

Ejemplo 5.2 Estación de trabajo. En una estación de trabajo con un único procesador se ejecutan programas (que se supone prácticamente su única carga de trabajo) con tiempo de CPU de distribución exponencial de media 3 minutos. Los programas se atienden según una disciplina FIFO. Sabiendo que las llegadas de programas a la estación se producen según un proceso de Poisson con una intensidad de 15 programas cada hora, por término medio, se pide:

¿Cuál es la probabilidad de que haya más de dos programas en espera de ejecución (además del que se está ejecutando)?
Calcular el tiempo medio que transcurre desde que se envía un programa al servidor hasta que se termina su ejecución. ¿Cuál es la relación entre este tiempo y el tiempo medio de CPU?
Calcular la probabilidad de que el programa esté en el servidor (esperando o ejecutándose) más de 10 minutos.
¿Cuál es el número medio de programas que están a la espera de comenzar a ejecutarse?
Obtener las respuestas a los apartados anteriores suponiendo que ahora se ha incrementado la llegada de programas hasta 18 a la hora, por término medio. En este caso utilizaremos la librería queueing para los cálculos numéricos. Si tomamos como unidad de tiempo las horas tendremos que $\lambda = 15$ y $1/\mu = 3 /60$, con lo cual $\mu = 20.$

# tasas en horas
lambda=15; mu=20; n=10
# Definición del entorno
env.MM1 <- NewInput.MM1(lambda = lambda, mu = mu, n = n)
# Características del sistema
s.MM1 <- QueueingModel(env.MM1)

Para responder a la cuestión 1 debemos calcular:

\[P(N_q \geq 2) = P(N \geq 3) = 1 - P(N \leq 2)\]

1- sum(s.MM1$Pn[1:3])

## [1] 0.421875

Para el primer apartado de la segunda cuestión sólo necesitamos el valor de $W$, o tiempo medio de permanencia en el sistema:

s.MM1$W

## [1] 0.2

El tiempo medio en el sistema es de 0.2 horas o 12 minutos. Para responder a la segunda pregunta hay que tener en cuenta que el tiempo de CPU corresponde con el tiempo de servicio, $1/\mu$, es decir, la relación buscada es:

\[\frac{W}{1/\mu}\]

s.MM1$W/(1/mu)

## [1] 4

Cada proceso está en la estación un tiempo equivalente a cuatro veces su tiempo de CPU.

Para respondear al tercer apartado debemos calcular (expresado en las unidades de tiempo utilizadas:

\[P(T > 10/60)\] Dicha probabilidad se obtiene a partir de la función de distribución de los tiempos de permanencia en el sistema:

t=10/60 # en horas
1 - s.MM1$FW(t)

## [1] 0.4345982

La cuarta cuestión se corresponde con el valor medio de la cola, esto es $L_q$:

s.MM1$Lq

## [1] 2.25

de forma que el número de procesos en espera es de 2.25.

Para responder al quinto apartado debemos cambiar el valor de la tasa de llegadas y volver a hacer los cálculos:

# Definición del entorno
lambda=18;mu=20;n=10
env.MM1 <- NewInput.MM1(lambda = lambda, mu = mu, n = n)
# Características del sistema
s.MM1 <- QueueingModel(env.MM1)
# Cuestión 1
1- sum(s.MM1$Pn[1:3])

## [1] 0.729

# Cuestión 2.1
s.MM1$W

## [1] 0.5

# Cuestión 2.2
s.MM1$W/(1/20)

## [1] 10

# Cuestión 3
1 - s.MM1$FW(10/60)

## [1] 0.7165313

# Cuestión 4
s.MM1$Lq

## [1] 8.1

Como puede verse numéricamente, el sistema está bastante más congestionado ahora. Podemos representar gráficamente ambas soluciones.

# Primer sistema
env.MM1 <- NewInput.MM1(lambda = 15, mu = 20, n = 10)
s.MM1.1 <- QueueingModel(env.MM1)
# Segundo sistema
env.MM2 <- NewInput.MM1(lambda = 18, mu = 20, n = 10)
s.MM1.2 <- QueueingModel(env.MM2)
# Establecemos secuencia de tiempos pra el análisis
tiempos <- seq(0, 4, 0.01)
# Almaceamos los resultados
sistema <- data.frame(tiempos = tiempos, 
                      FW1 = s.MM1.1$FW(tiempos),
                      FWq1 = s.MM1.1$FWq(tiempos),
                      FW2 = s.MM1.2$FW(tiempos),
                      FWq2 = s.MM1.2$FWq(tiempos))
# gráficos
g1 <- ggplot(sistema, aes(tiempos, FW1)) +
  geom_line(linetype = 1) +
  geom_line(aes(tiempos, FW2), linetype = 2) +
  labs(x = "Tiempo (en horas)", y = "Probabilidad", title = "W(t)")
g2 <- ggplot(sistema, aes(tiempos, FWq1)) +
  geom_line(linetype = 1) +
  geom_line(aes(tiempos, FWq2), linetype = 2) +
  labs(x = "Tiempo (en horas)", y = "Probabilidad", title = "Wq(t)")
grid.arrange(g1, g2, ncol = 2)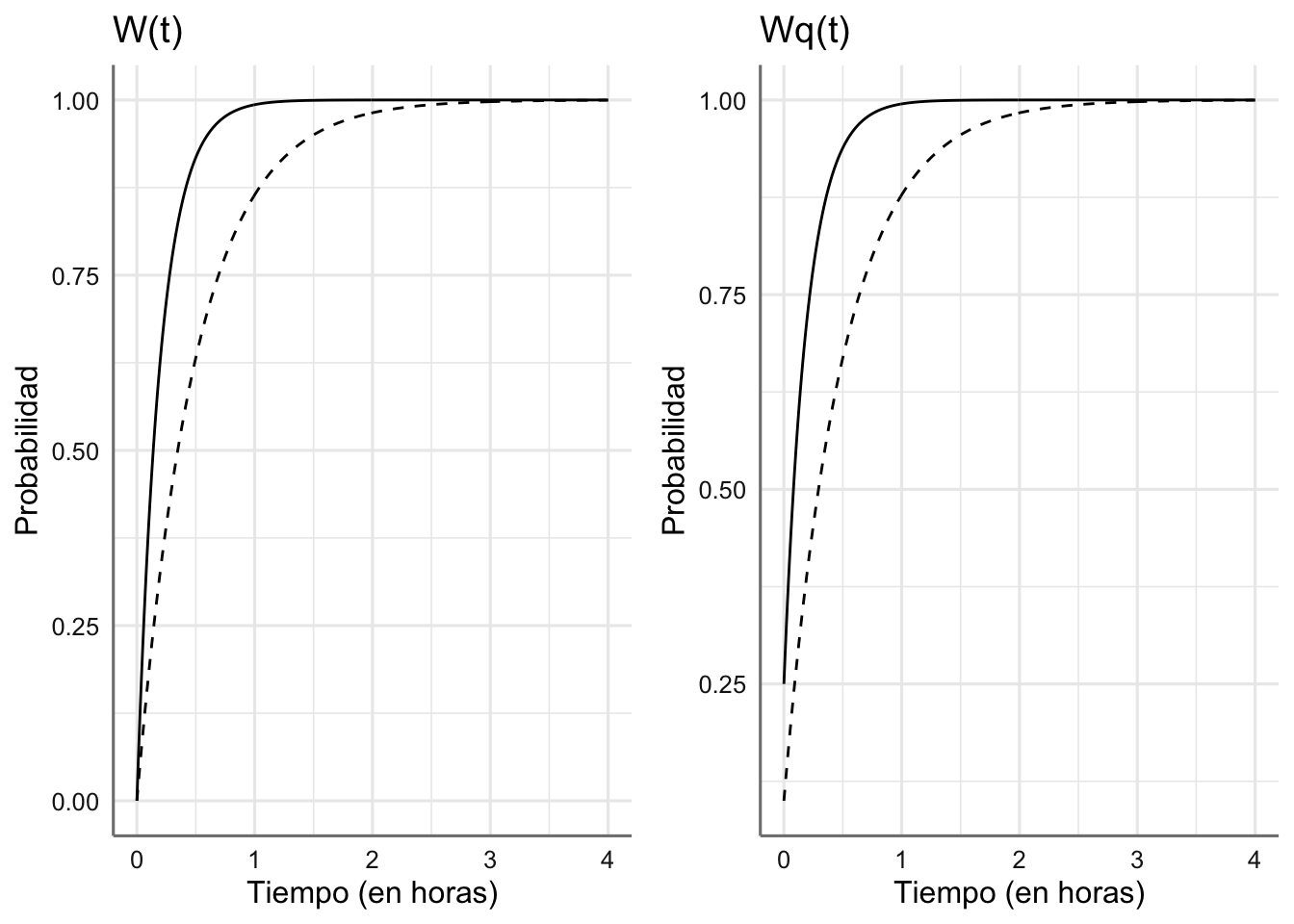

Figura 5.1: Funciones de distribución de W y Wq para ambos sistemas (Sistema 1 = línea continua, Sistema 2 = línea discontinua.

Como se puede ver, los tiempos medios de espera de los clientes en el sistema y en la cola para la segunda opción tienen probabilidades más bajas a lo largo del tiempo, lo que indica que el sistema está más congestionado porque los tiempos de atención son superiores (valores donde se alcanza la probabilidad 1).

5.3.2 M/M/1/K

Se trata de un modelo como el $M/M/1$, ya estudiado, pero con limitación $K$ para el tamaño de la cola. Es decir, la distribución del tiempo entre dos intentos de llegadas al sistema de clientes consecutivos es un PP de tasa $\lambda$, mientras que la distribución del tiempo de servicio es exponencial de media $1/\mu$ y sólo hay un servidor. Además el número de clientes que pueden estar en la cola es como mucho $K$, la población potencial es infinita y la disciplina es FIFO. Obviamente, en este modelo se puede dar el caso de que un cliente que intente entrar en el sistema no lo consiga, por estar la cola llena.

En esta situación tenemos que las tasas de llegadas viene dadas por:

\[ \lambda_n = \begin{cases} \lambda & \text{ si } n = 0, 1,...,K\\ 0 & \text{ si } n \geq K+1, \end{cases} \] mientras que las tasas de servicio se corresponden con las de la cola $M/M/1$

\[ \mu_n = \mu, \quad n = 1, 2,... \]

Así, el parámetro $c_n$ que da lugar a la distribución estacionaria es: \[ c_n = \begin{cases} \rho^n & \text{ si } n = 0, 1,...,K, K+1\\ 0 & \text{ si } n = K+2, K+3,... \end{cases} \] En este caso, por muy frecuente que sea la llegada de clientes al sistema en relación con la capacidad del servidor para dar servicio, la propia limitación en el tamaño de la cola fuerza a la estacionariedad, pues lo peor que podríamos imaginar es que prácticamente todo el tiempo estuviese el sistema saturado (es decir $P(N = K + 1) = 1$). Para analizar el comportamiento de la serie distinguiremos que $\rho \neq 1$ y $\rho = 1$.

Caso $\rho \neq 1$

En este caso la distribución de probabilidad de la variable aleatoria del “número de clientes en el sistema” es:

\[ P(N = n) = p_n = \begin{cases} \frac{\rho - 1}{\rho^{K+2} - 1} \rho^n & \text{ si } n = 0, 1,..., K+1\\ 0 & \text{ si } n = K+2, K+3,... \end{cases} \]

El número medio de clientes en el sistema es:

\[L = \frac{\rho}{1 - \rho} - \frac{(K + 2)\rho^{K+2}}{1 - \rho^{K+2}}\]

Dado que las tasas de llegada no son contantes, necesitamos obtener el valor de $\bar{\lambda}$ para aplicar la fórmula de Little al resto de cantidades de interés. En este caso:

\[\bar{\lambda} = \frac{\lambda(\rho^{K+1} - 1)}{\rho^{K+1} - 1}.\]

A partir de esta expresión podemos obtener el tiempo medio de espera de los clientes en la cola como:

\[W = \frac{1}{\mu - \lambda} - \frac{(K+1)\rho^{K+2}}{\lambda(1-\rho^{K+1})}.\]

De la relación entre $W$ y $W_q$ podemos obtener:

\[W_q = \frac{\lambda}{\mu(\mu - \lambda)} - \frac{(K+1)\rho^{K+2}}{\lambda(1-\rho^{K+1})}.\] Por último:

\[L_q = \frac{\rho^2}{1 - \rho} - \frac{(K + 1 + \rho)\rho^{K+2}}{1 - \rho^{K+2}}.\]

Caso $\rho = 1$

En este caso las fórmulas anteriores se simplifican a:

\[p_n = \frac{1}{K+2}, \text{ para } n = 0, 1,...,K + 1\] \[L = \frac{K + 1}{2}\] \[\bar{\lambda} = \frac{\lambda(K + 1)}{K + 2}\]

\[W = \frac{K + 2}{2\lambda}\] \[W_q = \frac{K}{2\lambda}\] \[L_q = \frac{K(K + 1)}{2(K+2)}\]

En este modelo (y en otros posteriores) el significado de $\rho$ como intensidad de tráfico se desvirtúa. Aquí $\rho$ no puede interpretarse como el cociente entre número medio de llegadas de clientes al sistema por unidad de tiempo y el número medio de clientes a los que el servidor tendría capacidad de dar servicio por unidad de tiempo, sino más bien como un cociente similar, pero donde el númerador representa el número medio de intentos de llegada, más que de llegadas efectivas al sistema. De hecho, por este motivo $\rho$ puede ser mayor o igual que 1, aún siendo el sistema estacionario. El valor de $\bar{\lambda}$ sí representa el número medio de entradas efectivas de clientes en el sistema por unidad de tiempo, y así la verdadera intensidad de tráfico podría medirse a través de:

\[ \bar{\rho} = \frac{\bar{\lambda}}{\mu} = \begin{cases} \frac{K+1}{K+2} & \text{ si } \rho = 1 \\ \frac{\rho^{K+2}-\rho}{\rho^{K+2}-1} & \text{ si } \rho \neq 1 \end{cases} \] que efectivamente sí es siempre menor que 1.

Ejemplo 5.3 Taller Mecánico. En un taller mecánico llegan vehículos para una puesta a punto antes de pasar la ITV, las llegadas siguen un proceso de Poisson de promedio 18 vehículos/hora. Las dimensiones del taller sólo permiten que haya 4 vehículos, y las ordenanzas municipales no permiten esperar en la vía pública. El taller despacha un promedio de 6 vehículos/hora de acuerdo con una distribución exponencial. Se pide:

¿Cuál es la probabilidad de que no haya ningún vehículo en el taller?
¿Cuál es el promedio de vehículos en el taller?
¿Cuánto tiempo pasa por término medio un vehículo en el taller?
¿Cuánto tiempo esperan por término medio los vehículos en la cola?
¿Cuál es la longitud media de la cola?

Se trata de un sistema $M/M/1/K$ con $K = 4$, y utilizaremos la librería queueing para los cálculos numéricos. Si tomamos como unidad de tiempo las horas tendremos que $\lambda = 18$ y $\mu = 6$. Geenramos el sistema de cola definido y procedemos con los cálculos solicitados.

# Definición del entorno
lambda=18;mu=6;k=4
env.MM1K <- NewInput.MM1K(lambda = lambda, mu = mu, k = k)
# Características del sistema
s.MM1K <- QueueingModel(env.MM1K)

Las medidas proporcionadas por la función son las mismas que con el modelo $M/M/1$. Comenzamos a responder las preguntas:

1. La probabilidad de que no haya ningún vehículo en el taller es $p_0$:

s.MM1K$Pn[1]

## [1] 0.008264463

1. Obtenemos el número medio de vehículos en el sistema $L$:

s.MM1K$L

## [1] 3.520661

1. Nos preguntan por el tiempo medio de permanencia en el sistema ($W$):

s.MM1K$W

## [1] 0.5916667

1. Respondemos con el tiempo medio de estancia en la cola ($W_q$):

s.MM1K$Wq

## [1] 0.425

1. En este caso estamos interesados en el número medio de clientes en la cola ($L_q$):

s.MM1K$Lq

## [1] 2.528926

Para el resto de sistemas de colas que vamos a presentar, no desarrollaremos de forma completa todas las fórmulas teóricas, y nos centraremos en los resultados numéricos que proporciona la libreria queueing para la resolución de aplicaciones.

5.4 Colas con múltiples servidores

Generalizamos los modelos anteriores a situaciones donde tenemos múltiples servidores.

5.4.1 M/M/s

Es una generalización del modelo $M/M/1$ en el caso en que haya $s$ servidores. Se trata pues de una cola en la que la distribución del tiempo entre llegadas consecutivas es una $Exp(\lambda)$, la distribución del tiempo de servicio es $Exp(\mu)$, y hay $s$ servidores. En este caso la población potencial y la capacidad de la cola son infinitas y la disciplina de la cola es FIFO.

Las tasas de llegadas vienen dadas por

\[\lambda_n = \lambda, \text{ para } n = 0, 1,...\] y las tasas de servicio

\[\mu_n = \begin{cases} n\mu & \text{ si } n = 1, 2,...,s\\ s\mu & \text{ si } n = s+1, s+2,... \end{cases} \]

con ratio de ocupación

\[\rho = \frac{\lambda}{\mu s}.\]

El parámetro $c_n$ que da lugar a la distribución estacionaria resulta: \[ c_n = \begin{cases} \frac{\lambda^n}{n!\mu^n} & \text{ si } n = 0, 1,...,s\\ \frac{\lambda^s}{s!\mu^s}\rho^{n-s} & \text{ si } n = s+1, s+2,... \end{cases} \]

La suma de la serie de los $c_n$ será convergente (el sistema es estacionario) si $\rho < 1$, es decir, $\lambda < s\mu$.

Ejemplo 5.4 Planta de fabricación. En una determinada planta de fabricación el último proceso consiste en una operación de pintura. En el centro de pintura siempre hay dos trabajadores que trabajan en paralelo, aunque debido a la configuración física, no pueden ayudarse mutuamente. Las llegadas al centro de pintura se producen según un proceso de Poisson con una tasa de llegada 100 unidades al día. Cada trabajador tarda una media de 27 minutos en pintar cada artículo. Últimamente, el exceso de trabajo en curso es motivo de preocupación, por lo que la dirección está considerando ampliar el centro de pintura y contratar a un tercer trabajador (se supone que el tercer trabajador, tras un periodo de formación, también tardará una media de 27 minutos por pieza). Otra opción sería comprar un robot para realizar la tarea de los trabajadores, ya que se sabe que el tiempo medio que tardará en cada pieza es de 10 minutos.

Analiza cada uno de los tres sistemas respecto de las medidas de eficiencia e indica que alternativa reduciría el inventario.
El coste del inventario (incluyendo la pieza que se está trabajando) se estima en 0,50 euros por pieza y hora. El coste por trabajador (salario y gastos generales) se estima en 40.000 euros al año, y el coste de instalación y mantenimiento de un robot se estima en 100.000 euros al año ¿Qué alternativa, si es que hay alguna, es justificable utilizando un criterio de coste esperado a largo plazo?

Se proponen tres sistemas de colas con las características siguientes (utilizando como unidad de tiempo las horas):

Situación 1. Cola $M/M/2$ con $\lambda = 100/24$ y $\mu = 60/27$
Situación 2. Cola $M/M/3$ con $\lambda = 100/24$ y $\mu = 60/27$
Situación 3. Cola $M/M/1$ con $\lambda = 100/24$ y $\mu = 60/10$

Para determinar qué sistema mejoraría el estado del inventario utilizamos varias medidas relativas a cada uno de ellos:

ratio de ocupación,
probabilidad de que el sistema este ocupado,
tiempo medio de las piezas en el sistema.

Definimos los tres sistemas y obtenemos las medidas de interés. Para los sistemas $M/M/s$ utilizaremos la función NewInput.MMC, donde el parámetro $c$ indica el número de servidores. Generamos los tres sistemas:

# Parámetros de los sistemas
lambda <- 100/24
muk <- 60/27
mu1 <- 60/10

# M/M/2
env.MM2 <- NewInput.MMC(lambda = lambda, mu = muk, c = 2, n = 2)
s.MM2 <- QueueingModel(env.MM2)
# M/M/3
env.MM3 <- NewInput.MMC(lambda = lambda, mu = muk, c = 3, n = 3)
s.MM3 <- QueueingModel(env.MM3)
# M/M/1
env.MM1 <- NewInput.MM1(lambda = lambda, mu = mu1, n = 1)
s.MM1 <- QueueingModel(env.MM1)

Obtenemos y comparamos las diferentes medidas consideradas

# ratio de ocupación
c(s.MM2$RO, s.MM3$RO, s.MM1$RO)

## [1] 0.9375000 0.6250000 0.6944444

# Probabildid de que el sistema este ocupado
c(1-s.MM2$Pn[1], 1-s.MM3$Pn[1], 1-s.MM1$Pn[1])

## [1] 0.9677419 0.8677686 0.6944444

# Tiempo medio en el sistema
c(s.MM2$W, s.MM3$W, s.MM1$W)

## [1] 3.7161290 0.6049587 0.5454545

Desde el punto de vista del ratio de ocupación, el mejor sistema sería el de tres trabajores, pero si utilizamos los otros dos criterios el mejor sistema sería el que utiliza el robot.

Hacemos ahora la evaluación de costes por hora teniendo en cuenta que cada año tiene 8760 horas (365*24). Para obtener los costes asociados debemos estimar el número de piezas en el sistema por hora para evaluar el coste total de inventario, y añadir el coste de la mano de obra. En esta situación tenemos:

# Coste M/M/2
s.MM2$L*0.50 + 2*(40000/8760)

## [1] 16.87436

# Coste M/M/3
s.MM3$L*0.50 + 3*(40000/8760)

## [1] 14.95896

# Coste M/M/1
s.MM3$L*0.50 + (100000/8760)

## [1] 12.67586

Atendiendo a los costes, el modelo que utiliza el robot genera un menor coste por hora, por lo que resulta el más beneficioso.

5.4.2 M/M/s/K

Es una generalización del modelo $M/M/1/K$, en el caso en que hay $s$ servidores. Las tasas de llegada son casi idénticas a las del modelo $M/M/1$, mientras que las de servicio son exáctamente iguales a las de un $M/M/s$:

\[\lambda_n = \begin{cases} \lambda \text{ para } n = 0, 1,..., K+s-1\\ 0 \text{ para } n = K+s, K+s+1,... \end{cases} \]

\[\mu_n = \begin{cases} n\mu & \text{ si } n = 1, 2,...,s\\ s\mu & \text{ si } n = s+1, s+2,... \end{cases} \]

con ratio efectivo de ocupación

\[\bar{\rho} = \frac{\bar{\lambda}}{\mu s}\]

Este sistema siempre es estacionario. A continuación, se presenta un ejemplo de este sistema y analizamos este tipo de cola.

Ejemplo 5.5 Centralita. Por razones técnicas, una centralita con dos operadoras sólo permite mantener tres llamadas en espera (de tal forma que cualquier llamada producida cuando ya hay dos que están siendo atendidas por las operadoras y otras tres en espera, recibe el tono de “línea ocupada”). Las llamadas llegan según un proceso de Poisson, a razón de 6 por minuto, siendo 15 segundos la media del tiempo que tarda cada operadora en direccionar una llamada, según una distribución exponencial. Calcular:

El porcentaje de tiempo que cada operadora está ocupada y el número medio de operadoras ocupadas.
El número medio de llamadas en espera.
La probabilidad de que una llamada obtenga la señal de “línea ocupada.”
Calcular las tres cantidades anteriores bajo el supuesto de que se amplíe a 5 las posibles llamadas en espera.

Para el análisis de este sistema utilizamos la función NewInput.MMCK, donde además de las tasas, debemos indicar el número de servidores, y la capacidad del sistema. Tomaremos como unidad de tiempo los minutos, de forma que $\lambda = 6$ y $\mu = 60/15 = 4$. La capacidad del sistema es $K = 5$ que se corresponde con dos llamadas atendidas y tres en espera. Se trata pues de un sistema $M/M/2/5$.

# M/M/2/5
env.MM25 <- NewInput.MMCK(lambda = 6, mu = 4, c = 2, k = 5)
s.MM25 <- QueueingModel(env.MM25)

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

Veamos cómo responder a cada una de las cuestiones planteadas, utilizando los resultados del sistema diseñado.

Para responder la primera cuestión, debemos obtener el ratio efectivo de ocupación, así como la diferencia entre el número medio de clientes en el sistema y el número medio de clientes en la cola, para determinar el número medio de servidores ocupados.

# Porcentaje de tiempo servidor ocupado: ratio de ocupación
round(100*s.MM25$RO, 2)

## [1] 68.62

# Número medio de servidores ocupados
s.MM25$L - s.MM25$Lq

## [1] 1.372329

La ocupación de cada operadora es del 68.6% y el número medio de operadores ocupados es del 1.4.

Con respecto al número medio de llamadas en espera tenemos:

# Número medio de llamadas en espera
s.MM25$Lq

## [1] 0.6336252

En cuanto a la probabilidad solicitada debemos calcular $P(N_q = 3) = P(N = 5)$ que se obtiene como:

# Probabilidad de linea ocupada
s.MM25$Pn[6]

## [1] 0.08511384

Tan solo en un 8.5% de las ocasiones salta el mensaje de línea ocupada, es decir, el sistema esta ocupado al 100% la mayor parte del tiempo.

Evaluamos ahora el incremento del tamaño de sistema aumentado las llamadas en espera, y extraemos conclusiones.

# M/M/2/7
env.MM27 <- NewInput.MMCK(lambda = 6, mu = 4, c = 2, k = 7)
s.MM27 <- QueueingModel(env.MM27)

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

## Warning in formals(fun): argument is not a function

# Porcentaje de tiempo servidor ocupado
round(100*s.MM27$RO, 2)

## [1] 71.77

# Número medio de servidores ocupados
s.MM27$L - s.MM27$Lq

## [1] 1.435402

# Número medio de llamadas en espera
s.MM27$Lq

## [1] 1.014966

# Probabilidad de linea ocupada
s.MM27$Pn[8]

## [1] 0.04306559

5.5 Redes de colas en serie

Una red de colas en serie es una colección de $K$ colas que se suceden unas a otras, de tal manera que sólo es posible la entrada de clientes dede fuera del sistema a la primera de ellas, produciéndose la salida de ellas tras el servicio de la última cola. En esta situación podemos definir las medidas de eficiencia del sistema completo de colas en función de las medidas de eficencia de cada una de las colas que conforman el sistema, teniendo en cuenta que tan sólo hay una tasa de llegada que corresponde con la cola inicial de la red.

Imaginemos $i=1,2,...,k$ colas en red del tipo $M/M/s_i$, independientes, con tasa de entrada $\lambda$ y tasa de servicio $\mu_i$, y con medidas de eficiencia $L_i, W_i, L_{q_i}, W_{q_i}$. Dado que en este caso el flujo de un cliente a través de la red es secuencial, será cierto que los tiempos medios de un cliente en la red son la suma de los correspondientes a cada subsistema. Si denotamos por $L_{red}, W_{red}, L_{q_{red}}, W_{q_{red}}$ las medidas de eficiencia del sistema, aplicando este razonamiento tenemos que:

\[L_{red} = \sum_{i = 1}^k L_i\]

\[W_{red} = \sum_{i = 1}^k W_i\]

\[W_{q_{red}} = W_{red} - \left(\sum_{i = 1}^k \frac{1}{\mu_i}\right)\]

\[L_{q_{red}} = \lambda W_{q_{red}}.\]

De esta forma basta, analizar la red consistirá en analizar cada una de las colas que la conforman.

Ejemplo 5.6 Empresa ITV. Una empresa de ITV en una localidad dispone de una superficie que consta de tres partes. a) Una caseta donde los clientes entregan la documentación del vehículo y realizan el pago de tasas, sin restricciones paa atender ningún vehículo. Una nave formada por dos circuitos, b) revisión y c) oficina de personal técnico, atendidos por dos técnicos cada uno de ellos. Los vehículos que llegan a la nave son atendidos con una tasa de servicio medio de 45 clientes/hora para la revisión y 2 minutos/cliente en la oficina de personal técnico. Los coches acuden a la ITV a una media de 57 clientes/hora, ya que un mayor número de vehículos colapsaría el trabajo de la caseta, cuyo empleado atiende a un ritmo medio de 1 cliente/minuto. Las llegadas siguen un Proceso de Poisson y los tiempos de servicio se distribuyen según una variable exponencial. Se pide:

Factor de utilización o intensidad de tráfico en cada nodo de la red.
Probabilidades de que no haya ningún cliente en cada uno de los nodos de la red.
Longitud media de la cola de vehículos que habiendo pagado las tasas se encuentran esperando a la entrada de la nave.
Tiempo medio que un cliente pasa en la revisión.
Tiempo medio que un cliente pasa en la oficina de personal técnico.
Tiempo medio que un cliente se encuentra en la ITV.
Para agilizar el proceso, la empresa estudia la posibilidad de ampliar el número de servidores en la caseta o en la oficina. Suponiendo que el coste de ampliación en uno u otro lugar fuera equivalente, ¿qué criterio sería más acertado para que el tiempo de servicio del sistema fuera menor?

El sistema se puede describir com una red de colas en serie con nodos: caseta ($M/M/1$), equipamiento ($M/M/2$) y personal técnico ($M/M/2$), con tasas de llegadas y servicio (expresadas en minutos) dadas por:

\[\lambda_1 = \lambda_2 = \lambda_3 = 57/60 = 0.95\]

\[\mu_1 = 1; \mu_2 = 45/60 = 0.75; \mu_3 = 1/2 = 0.5\]

Planteamos los tres sistemas de colas y obtenemos las correspondientes medidas de eficiencia:

# M/M/1
nodo1 <- QueueingModel(NewInput.MM1(lambda = 0.95, mu = 1, n = 15))
# M/M/2
nodo2 <- QueueingModel(NewInput.MMC(lambda = 0.95, mu = 0.75, c = 2, n = 15))
# M/M/2
nodo3 <- QueueingModel(NewInput.MMC(lambda = 0.95, mu = 0.5, c= 2, n = 15))
# Medidas de eficiencia de cada nodo
ef.nodo1 <- c(nodo1$RO, nodo1$L, nodo1$Lq, nodo1$W, nodo1$Wq, nodo1$Pn[1]) 
ef.nodo2 <- c(nodo2$RO, nodo2$L, nodo2$Lq, nodo2$W, nodo2$Wq, nodo2$Pn[1]) 
ef.nodo3 <- c(nodo3$RO, nodo3$L, nodo3$Lq, nodo3$W, nodo3$Wq, nodo3$Pn[1])
eficiencia <- data.frame(rbind(ef.nodo1, ef.nodo2, ef.nodo3))
names(eficiencia) <-c("Ro", "L", "Lq", "W", "Wq","P_0") 
eficiencia

##                 Ro         L         Lq         W         Wq        P_0
## ef.nodo1 0.9500000 19.000000 18.0500000 20.000000 19.0000000 0.05000000
## ef.nodo2 0.6333333  2.115028  0.8483612  2.226345  0.8930118 0.22448980
## ef.nodo3 0.9500000 19.487179 17.5871795 20.512821 18.5128205 0.02564103

5.6 Funciones simmer

En este apartado se presentan los algoritmos de simulación de simmer para los sistemas de colas estudiados.

5.6.1 M/M/1

library(simmer)
library(simmer.bricks)

# Sistema
#################################################
cola.MM1 <- function(t, lambda, mu)
{
  # lambda: tasa de llegadas
  # mu: tasa de servicio

  # Funciones de tiempos
  tarrival <- function() rexp(1, lambda)
  tserver <- function() rexp(1, mu)
  
  # Trayectoria de servicio
  servicio <- trajectory() %>%
    visit("server", tserver)               

  # Entorno del sistema 
  #################################################
  simmer() %>%
    add_resource("server", capacity = 1, queue_size = Inf) %>%           
    add_generator("arrival", servicio, tarrival) %>% 
    run(until = t)     
}

5.6.2 M/M/1/K

# Sistema
#################################################
cola.MM1K <- function(t, lambda, mu, K)
{
  # lambda: tasa de llegadas
  # mu: tasa de servicio
  # K: capacidad del sistema

  # Funciones de tiempos
  tarrival <- function() rexp(1, lambda)
  tserver <- function() rexp(1, mu)
  
  # Tamaño de la cola
  qsize <- K - 1
  
  # Trayectoria de servicio
  servicio <- trajectory() %>%
    visit("server", tserver)               

  # Entorno del sistema 
  #################################################
  simmer() %>%
    add_resource("server", capacity = 1, queue_size = qsize) %>%           
    add_generator("arrival", servicio, tarrival) %>% 
    run(until = t)     
}

5.6.3 M/M/s

# Sistema
#################################################
cola.MMs <- function(t, lambda, mu, s)
{
  # lambda: tasa de llegadas
  # mu: tasa de servicio
  # s: servidores idénticos disponibles

  # Funciones de tiempos
  tarrival <- function() rexp(1, lambda)
  tserver <- function() rexp(1, mu)
  
  # Trayectoria de servicio
  servicio <- trajectory() %>%
    visit("server", tserver)               

  # Entorno del sistema 
  #################################################
  simmer() %>%
    add_resource("server", capacity = s, queue_size = Inf) %>%           
    add_generator("arrival", servicio, tarrival) %>% 
    run(until = t)     
}

5.6.4 M/M/s/K

# Sistema
#################################################
cola.MMsK <- function(t, lambda, mu, s, K)
{
  # lambda: tasa de llegadas
  # mu: tasa de servicio
  # s: servidores
  # K: capacidad del sistema

  # Funciones de tiempos
  tarrival <- function() rexp(1, lambda)
  tserver <- function() rexp(1, mu)
  
  # Tamaño de la cola
  qsize <- K - s
  
  # Trayectoria de servicio
  servicio <- trajectory() %>%
    visit("server", tserver)               

  # Entorno del sistema 
  #################################################
  simmer() %>%
    add_resource("server", capacity = s, queue_size = qsize) %>%           
    add_generator("arrival", servicio, tarrival) %>% 
    run(until = t)     
}

5.7 Ejercicios

5.7.1 Básicos

Ejercicio B5.1. Para el ejemplo del sistema de la Estación de trabajo descrito para el sistema $M/M/1$ [@ref((exm:colas002)], contestar a las diferentes cuestiones que allí se planteaban pero considerando que la estación de trabajo dispone de tres servidores idénticos. Hallar también el número medio total de procesos en la estación.

Ejercicio B5.2. Los coches llegan a un peaje 24 horas al día según un proceso de Poisson con una tasa media de 15 por hora. Estamos interesados en:

¿Cuál es el número esperado de coches que llegarán a la cabina entre la 1:00 p.m. y 1:30 p.m.?
¿Cuál es el tiempo esperado entre dos coches que llegan consecutivamente?
Son las 13:12 y acaba de llegar un coche. ¿Cuál es el número esperado de coches que llegarán entre este momento y la 1:30 p.m.?
Son las 13:12 y acaba de llegar un coche. ¿Cuál es la probabilidad de que lleguen dos coches ,más hasta las 13:30?
Son las 13:12 y el último coche en llegar lo hizo a las 13:05. ¿Cuál es la probabilidad de que no lleguen más coches hasta las 13:30?
Son las 13:12 y el último coche en llegar lo hizo a las 13:05. ¿Cuál es la tiempo esperado entre la llegada del último coche y la del siguiente?

Ejercicio B5.3. Una tienda de alimentación es atendida por una persona. Aparentemente el patrón de llegadas de clientes durante los sábados se comporta siguiendo un proceso de Poisson con una tasa de llegadas de 10 personas por hora. A los clientes se les atiende siguiendo un orden tipo FIFO y debido al prestigio de la tienda, una vez que llegan estan dispuestos a esperar el servicio. Se estima que el tiempo que se tarda en atender a un cliente se distribuye exponencialmente, con un tiempo medio de 4 minutos.

Determina:

La probabilidad de que haya alguien en la cola.
La longitud media de la cola.
Tiempo medio que un cliente permanece en la cola.

Ejercicio B5.4 Un asesor fiscal dispone de un local para atender a sus clientes, los cuales se concentran mayoritariamente entre los meses de mayo y junio. El local tiene una capacidad máxima de 8 asientos en espera, el cliente se va si no encuentra un asiento libre, y el tiempo entre llegadas de clientes se puede considerar distribuido exponencialmente con 20 clientes/hora en período punta. El tiempo de una consulta se distribuye exponencialmente con una media de 12 minutos.

¿Cuántas consultas por hora realizará en promedio?
¿Cuál es el tiempo medio de permanencia en el local?

Ejercicio B5.5. Un laboratorio de informática consta de 5 estaciones de trabajo. Cada estación se avería, por término medio, una vez cada 30 días, siendo exponencial (v.a.) el tiempo hasta la próxima avería. El laboratorio dispone de dos personas que, en caso de ser necesario, pueden arreglar estas averías. El tiempo de reparación de cada avería es exponencial, con media de 3 días. Calcular:

El número medio de estaciones funcionando.
El porcentaje de tiempo que cada uno de los técnicos puede dedicar a otras tareas ajenas a la reparación de las estaciones.

5.7.2 Avanzados

Ejercicio A5.1. Un gran hotel ha colocado un ordenador para uso de los clientes en una sala de atención al cliente. La llegada de clientes que necesitan utilizar el ordenador sigue un proceso de Poisson con una media de ocho clientes por hora. El tiempo que cada persona utiliza el ordenador es variable y se aproxima mediante una distribución exponencial, con un tiempo medio de 5 minutos entre llegadas consecutivas. El hotel está interesado en:

¿Cuál es la probabilidad de que la sala donde está el ordenador esté vacía?
¿Cuál es la probabilidad de que nadie esté esperando para utilizar el ordenador?
¿Cuál es el tiempo medio que un cliente debe esperar en la cola para utilizar el ordenador?
¿Cuál es la probabilidad de que un cliente que llega vea a dos personas esperando en cola?

Ejercicio A5.2. Una prensa de taladro en un taller de trabajo tiene piezas que llegan para ser taladradas de acuerdo con un proceso de Poisson con una tasa media de 15 piezas por hora. El tiempo medio que se tarda en completar cada pieza es una variable aleatoria con una función de distribución exponencial cuya media es de 3 minutos. Estamos interesados en conocer:

¿Cuál es la probabilidad de que el taladro esté ocupado?
¿Cuál es el número medio de piezas en espera de ser taladradas?
¿Cuál es la probabilidad de que al menos una pieza esté esperando para ser taladrada?
¿Cuál es el tiempo medio que pasa una pieza en la sala de taladrado?
A la empresa le cuesta 8 céntimos por cada minuto que pasa cada pieza en la sala de taladrado. Por un gasto adicional de 10 euros por hora, la empresa puede disminuir la duración media de la operación de taladrado a 2 minutos. ¿Merece la pena el coste adicional?

Ejercicio A5.3. En una fabrica existe una oficina de la Seguridad Social a la que los obreros tienen acceso durante las horas de trabajo. El jefe de personal, que ha observado la afluencia de obreros a la ventanilla, ha solicitado que se haga un estudio relativo al funcionamiento de este servicio. Se designa a un especialista para que determine el tiempo medio de espera de los obreros en la cola, y la duración media de la conversación que cada uno mantiene con el empleado de la ventanilla. Este analista llega a la conclusion de que durante la primera y la última media hora de la jornada la afluencia es muy reducida y fluctuante, pero que durante el resto de la jornada el fenómeno se puede considerar estacionario. Del analisis de 100 periodos de 5 minutos, sucesivos o no, pero situados en la fase estacionaria, se dedujo que el número medio de obreros que acudían a la ventanilla era de 1.25 por periodo (en media) y que el tiempo entre llegadas seguía una distribucion exponencial. Un estudio similar sobre la duración de las conversaciones, llevó a la conclusión de que se distribuían exponencialmente con duración media de 3.33 minutos. Determina:

Número medio de obreros en cola.
Tiempo medio de espera en la cola.
Compara el tiempo perdido por los obreros con el tiempo perdido por el oficinista. Calcula el coste para la empresa, si una hora de inactividad del oficinista vale 250 euros y una hora del obrero 400 euros.

Ejercicio A5.4. Una compañía ferroviaria pinta sus vagones, según lo van necesitando, en sus propios talleres, donde se pintan a mano, de uno en uno, a un ritmo medio de uno cada 4 horas (tiempos exponenciales) y con un coste anual de 4 millones de euros. Se ha determinado que los vagones pueden llegar según un proceso de Poisson a razón de uno cada 5 horas. Además el coste por cada vagón que no está activo es de 500 euros la hora.

Se plantean otras dos posibilidades. Una es encargar dicho trabajo a una empresa de pintura que lo haría con aerosol, con el consiguiente ahorro de tiempo (un vagón pintado cada 3 horas, con tiempos exponenciales). Sin embargo el presupuesto para esta segunda alternativa es de 10 millones de euros anuales. La otra opción es poner otro taller exactamente igual al que hay actualmente, con igual tasa de servicio y coste anual que permita pintar dos vagones a la vez.

En todos los casos el trabajo se considera ininterrumpido, esto es, se trabajan 24 × 365 = 8760 horas anuales. ¿Cuál de los tres procedimientos es más eficiente?

Ejercicio A5.5. Un taller utiliza 10 máquinas idénticas. Cada máquina deja de funcionar en promedio una vez cada 7 horas. Un operario puede reparar una máquina en 4 horas en promedio, pero el tiempo de reparación real varía según una distribución exponencial.

Responder y comentar las siguientes cuestiones de interés:

El número mínimo de mecánicos que se necesita para que el número medio de máquinas que fallan sea menor a 4.
El número mínimo de mecánicos que se necesitan para que la demora esperada hasta que se repare una máquina sea menor a 4 horas.

Ejercicio A5.6. Un estudiante trabaja como encargado de una biblioteca por las noches y es el único en el mostrador durante todo su turno de trabajo. Las llegadas al mostrador siguen una distribución de Poisson con una media de 8 por hora. Cada usuario de la biblioteca es atendido de uno en uno, y el tiempo de servicio sigue una distribución exponencial con una media de 5 minutos.

¿Cuál es la probabilidad de que se forme cola?
¿Cuál es la longitud media de la cola?
¿Cuál es el tiempo medio que un cliente pasa en la biblioteca hasta que le han atendido?
¿Cuál es el tiempo medio que un cliente pasa en la cola esperando a que le atiendan?
El estudiante pasa el tiempo en que no hay clientes clasificando artículos de revistas. Si puede clasificar 22 fichas por hora como media cuando trabaja de modo continuo, ¿cuántas fichas puede ordenar durante su jornada de 8 horas?

Ejercicio A5.7. Una compañía de alquiler de coches tiene un servicio de mantenimiento de coches (revisión del aceite, frenos, lavado…) que sólo es capaz de atender los coches de uno en uno, y que trabaja 24 horas al día. Los coches llegan al taller a un ritmo de 3 coches por día. El tiempo que dura el servicio de mantenimiento de un coche sigue una distribución exponencial de media 7 horas. El servicio de mantenimiento cuesta a la compañía 375 euros por día. La compañía estima en 25 euros/día el coste de tener el coche parado sin poderse alquilar. La compañía se plantea la posibilidad de cambiar el servicio de mantenimiento por uno más rápido que puede reducir el tiempo de mantenimiento a una media de 5 horas, pero esto también supone un incremento del coste. ¿Hasta que valor puede aumentar el coste para que la compañía contrate los nuevos servicios de mantenimiento?

Ejercicio A5.8. Nuestro local de comida rápida, “Panis,” tiene mucho que aprender sobre teoría de colas. Insta a los clientes a que formen 3 colas en las que se distribuyen de forma aleatoria delante de los empleados durante el periodo de comidas diario. Además han instalado barreras entre las tres colas para prevenir que la gente se “cambie de cola.” Llegan los clientes según una distribución de Poisson a un ritmo de 60 por hora y el tiempo en que un cliente es servido varía según una distribución exponencial de media 150 segundos.

Asumiendo el estado estacionario del sistema, ¿cuál es el tiempo medio de estancia del cliente hasta que ha sido atendido?
En el caso de que se optara por una una única cola para distribuir finalmente a los tres servidores (eliminando las barreras), ¿cuál sería el tiempo de espera en cola?

Ejercicio A5.9. Una organización está actualmente envuelta en el establecimiento de un centro de telecomunicaciones para mejorar su capacidad. El centro deberá ser el responsable de la salida de los mensajes así como de la entrada y distribución dentro de la organización. El encargado del centro es el responsable de determinar los operadores que deben trabajar en él. Los operarios encargados de la salida de mensajes son responsables de hacer pequeñas correcciones a los mensajes, mantener un índice de códigos y un fichero con los mensajes salientes en los últimos 30 días, y por supuesto, transmitir el mensaje. Se ha establecido que este proceso es exponencial y requiere una media de 28 min/mensaje. Los operarios de transmisión trabajarán en el centro 7 horas al día y cinco días a la semana. Todos los mensajes salientes serán procesados según el orden en que se vayan recibiendo según un proceso de Poisson con una media de 21 mensajes en 7 horas. Los mensajes deben ser atendidos en 2 horas como máximo. Determine el número mínimo de personal que se necesita para cumplir este criterio de servicio.

Ejercicio A5.10. La empresa “Refrigeración Hermanos Pérez” debe elegir entre dos tipos de sistema para el mantenimiento de sus camiones. Se estima que los camiones llegan al servicio de mantenimiento de acuerdo con una distribución exponencial de media 40 minutos, y que este ratio de llegada es independiente del sistema de servicio que se establezca. El primer tipo de sistema puede atender a dos camiones en paralelo, y a cada camión se le haría todo el mantenimiento en una media de 30 minutos (el tiempo sigue una distribución exponencial). En el segundo sistema sólo se podría atender a un camión, pero el tiempo medio en que se realizaría el mantenimiento sería de 15 minutos (distribución exponencial). Para ayudar al encargado de tomar la decisión, responde las siguientes cuestiones:

¿Cuántos camiones habrá por término medio en cualquiera de los dos sistemas?
¿Cuánto tiempo pasará cada camión en el taller en cualquiera de los dos sistemas?
El encargado estima que cada minuto que un camión pasa en el taller, reduce los beneficios en 2 euros. Se sabe que el sistema de dos camiones en paralelo tiene un coste de un euro por minuto. ¿Qué debería costar el segundo sistema para que no hubiera diferencia económica entre ellos?

Ejercicio A5.11. Una empresa que alquila ordenadores considera necesario revisarlos una vez al año. La primera alternativa, con un coste de 750.000€ es hacer un mantenimiento manual en el que cada ordenador necesitaría un tiempo que sigue una distribución exponencial con una media de 6 horas. La segunda opción sería un mantenimiento con máquinas, con un coste de un millón de euros; en este caso el tiempo de mantenimiento sería de 3 horas con una distribución exponencial. Para ambas alternativas los ordenadores llegan según un proceso de Poisson de tasa 3 al día. El tiempo en que está parado un ordenador tiene un coste de 150€ por hora. ¿Qué alternativa debe elegir la empresa? Se asume que la empresa trabaja 24 horas, 365 días al año.

Ejercicio A5.12. Un pequeño autoservicio de lavado en el que el coche que entra no puede hacerlo hasta que el otro haya salido completamente, tiene una capacidad de aparcamiento de 10 coches, incluyendo el que está siendo lavado. La empresa ha estimado que los coches llegan según un proceso de Poisson con una media de 20 coches/hora, y el tiempo de lavado sigue una distribución exponencial de 12 minutos. La empresa abre durante 10 horas al día. ¿Cuál es la media de coches perdidos cada día debido a las limitaciones de espacio?

Ejercicio A5.13. La compañía “Gasolinas y Aceites SA” es la encargada de descargar los barcos cargados de petróleo que llegan al puerto y llevarlo a la refinería. En el puerto tiene 6 muelles de descarga y 4 equipos para la descarga del barco. Cuando los muelles están llenos, los barcos se desvían a muelles de espera hasta que les toca su turno. Los barcos llegan según un proceso de Poisson de tasa uno cada 2 horas. Para descargar el barco se necesita una media de 10 horas, con variabilidad exponencial. La compañía desea saber los siguientes datos:

Por término medio, ¿cuántos barcos hay en el puerto?
Por término medio, ¿cuánto tiempo pasa un barco en el puerto?
¿cuál es la media de llegada de los barcos a los muelles de espera?
La compañía estudia la posibilidad de construir otro muelle de descarga. La construcción y mantenimiento del puerto costaría X€ al año. La compañía estima que desviar un barco hacia los muelles de espera cuando los muelles de descarga están llenos tiene un coste de Y€. ¿Cuál es la relación entre X e Y para que la compañía construya otro puerto de descarga?

Ejercicio A5.14. Uno de los hospitales de la ciudad de Valencia ofrece todos los miércoles por la noches revisiones gratis de vista. Un test necesita, por término medio, 20 minutos exponencial. Los clientes llegan según un proceso de Poisson de tasa 6 por hora, y los pacientes se atienden según norma FIFO. Los encargados del hospital desean saber de cuánto personal sanitario deben disponer. Para ello quieren evaluar, para diferentes números de doctores: 1) ¿cuál es el número medio de gente esperando? 2) el tiempo medio que un cliente pasa en la clínica y 3) el tiempo medio que los doctores están parados.

Ejercicio A5.15. Una estación de ITV cuenta con tres puestos para inspección y en cada uno sólo puede ser atendido un coche. Cuando un coche sale de un puesto, la vacante es ocupada por otro que está en cola. La llegada de coches sigue un proceso de Poisson con una tasa de un coche por minuto. En el parking sólo caben 4 vehículos. El tiempo de inspección sigue una distribución exponencial de media 6 minutos. El inspector jefe desea saber el número medio de coches en la estación, el tiempo medio (incluida la inspección) de espera, y el número medio de coches en cola. ¿Cuántos coches tendrán que volver en otro momento?

Ejercicio A5.16. Al servicio de urgencias de un hospital los pacientes llegan según un Proceso de Poisson de tasa 3 pacientes/hora. El médico que está en dicho servicio los atiende a razón de 4 clientes/hora (tiempos exponenciales). ¿Contrataría o no a un segundo médico? Para responder a esta pregunta se deben comparar las siguientes características en ambos sistemas:

Probabilidad de que no se encuentren pacientes en el departamento de emergencias.
Probabilidad de que existan 3 pacientes en urgencias.
Tiempo total del cliente en urgencias.
Tiempo total de espera por en urgencias.
El número de pacientes en urgencias en un momento dado.
El número de pacientes en urgencias esperando a ser atendidos.
Probabilidad de que el paciente espere más de 1 hora.
Probabilidad de que el paciente espere más de 1 hora en ser atendido.

Ejercicio A5.17. Una base de mantenimiento de aviones dispone de recursos para revisar únicamente un motor de avión a la vez. Por tanto, para devolver los aviones lo antes posible a la pista, la política que se sigue consiste en aplazar la revisión de los 4 motores de cada avión, esto es, solamente se revisa un motor cada vez que un avión llega a la base. Con esta política, los aviones llegan al servicio de mantenimiento según un proceso de Poisson de tasa uno al día. El tiempo requerido para revisar un motor (una vez que se empieza el trabajo) tiene una distribucion exponencial de media 1/2 día. Se ha hecho una propuesta para cambiar la política de revisión, de manera que los 4 motores se revisen de forma consecutiva cada vez que un avión llegue a la base. A pesar de que ello supondría cuadruplicar el tiempo esperado de servicio, cada avión necesitaría ser revisado con una frecuencia 4 veces menor. Utliza las medidas descriptivas del sistema para comparar ambas políticas.

Ejercicio A5.18. Una pequeña estación de servicio junto a una autopista interestatal está abierta las 24 horas al día y tiene un surtidor y espacio para otros dos coches. El proceso de llegadas es un PP con tasa media de llegada de 8 coches/hora y el tiempo medio de servicio en el surtidor es una variable aleatoria exponencial de 6 minutos. El beneficio esperado de cada coche es de 5 dólares. Por 60 dólares más al día, el propietario de la estación puede aumentar la capacidad de los coches en espera en uno. Analiza cada uno de los sistemas propuestos y determina si merece la pena la inversión.

Ejercicio A5.19. Un centro de reparación dentro de una planta de fabricación está abierto las 24 horas del día y siempre hay una persona presente. La llegada de artículos que necesitan ser reparados en el centro de reparación se ajusta a un proceso de Poisson con una tasa media de 6 por día. La duración de la reparación de los artículos es muy variable y sigue una distribución exponencial con una media de 5 horas. La política de gestión actual es permitir un máximo de tres trabajos en el centro de reparación. Si hay tres trabajos en el centro y llega un cuarto, el trabajo se envía a un contratista externo que devolverá el trabajo 24 horas más tarde. Por cada día que un artículo está en el centro de reparaciones, le cuesta a la empresa 30 euros. Cuando un artículo se envía al contratista externo, le cuesta a la empresa 30 euros por el tiempo perdido, más 75 euros por la reparación. Contesta a las cuestiones siguientes:

Se ha sugerido que la dirección cambie la política para permitir cuatro trabajos en el centro; así los trabajos se enviarían al contratista externo sólo cuando hubiera cuatro acumulados ¿Es esta una política mejor?
¿Cuál sería la política de corte óptima? En otras palabras, ¿a qué nivel sería mejor enviar los trabajos excedentes al contratista externo?
El personal y el mantenimiento del centro de reparaciones durante las 24 horas del día cuestan 400 por día. ¿Es una política económica acertada o sería mejor cerrar el centro de reparaciones y utilizar sólo el contratista externo?

Ejercicio A5.20. Una pequeña tienda de informática tiene dos dependientes para atender a los clientes (pero capacidad infinita para retener a los clientes). Los clientes llegan a la tienda según un proceso de Poisson con una tasa media de 5 por hora. El 50% de los que llegan quieren comprar hardware y el 50% quiere comprar software. La política actual de la tienda es que un dependiente atiende sólo a los clientes de software y otro sólo a los clientes de hardware, por lo que la tienda actúa como dos sistemas M/M/1 independientes. Tanto si el cliente quiere hardware como software, el tiempo que pasa con uno de los dependientes de la tienda se distribuye exponencialmente con una media de 20 minutos. El propietario de la tienda está considerando cambiar la política de funcionamiento de la tienda y hacer que los dependientes ayuden tanto con el software como con el hardware; así, nunca habría dependiente inactivo cuando hubiera dos o más clientes en la tienda. La desventaja es que los dependientes serían menos eficientes, ya que tendrían que ocuparse de algunas cosas que no conocen. Se calcula que el cambio aumentaría el tiempo medio de servicio a 21 minutos.

Si el objetivo es minimizar el tiempo de espera de un cliente, ¿qué política es la mejor?
Si el objetivo es minimizar el número esperado de clientes en la tienda, ¿qué política es la mejor?

Ejercicio A5.21. Los clientes llegan a una cola de una estación a un ritmo de cinco por hora. Cada cliente necesita una media de 78 minutos de servicio.

¿Cuál es el número mínimo de servidores necesarios para mantener el sistema estable?
¿Cuál es el número esperado de servidores ocupados si el sistema emplea $s$ servidores ($1 \leq s \leq 10$)?
¿Cuántos servidores son necesarios si la legislación laboral estipula que un servidor no puede estar ocupado más del 80% del tiempo?

Ejercicio A5.22. Los clientes llegan a una barbería según un proceso de Poisson a un ritmo de ocho por hora. Cada cliente requiere 15 minutos de media. La barbería tiene cuatro sillas y un solo barbero. Un cliente no espera si todas las sillas están ocupadas. Suponiendo una distribución exponencial de los tiempos de servicio:

Calcula el tiempo esperado que pasa un cliente en la barbería.
Supongamos que el barbero cobra 12 euors por el servicio. Calcula la tasa de ingresos a largo plazo del barbero. (Pista: ¿Qué fracción de los clientes que llegan, pasan?)
Supongamos que el barbero contrata a un ayudante, por lo que ahora hay dos barberos. ¿Cuál es la nueva tasa de ingresos?
Supongamos que el barbero instala una silla más para que los clientes esperen. ¿Cuánto aumentan los ingresos debido a la silla adicional?

Ejercicio A5.23. Una máquina produce artículos de uno en uno, siendo los tiempos de producción iid exponenciales con media $1/\lambda$. Los artículos producidos se almacenan en un almacén de capacidad $K$. Cuando el almacén está lleno, la máquina se apaga, y se vuelve a encender cuando el almacén tiene espacio para al menos un artículo. La demanda de los artículos se produce según a un $PP(\mu)$. La demanda que no puede satisfacerse se pierde. Supongamos que el tiempo medio de tiempo de fabricación es de 1 hora y la tasa de demanda es de 20 artículos al día. Supongamos que la capacidad del almacén es de 10.

Calcula la fracción de tiempo que la máquina está apagada a largo plazo.
Calcula la fracción de la demanda perdida a largo plazo.
Cuando un artículo entra en el almacén, su valor es de 100 euros Sin embargo, pierde valor a razón de 1 euro por hora mientras espera en el almacén. Así, si un artículo ha estado en el almacén durante 10 horas cuando se vende, sólo alcanza 90 euros. Calcular los ingresos a largo plazo por hora.

Ejercicio A5.24. Una sucursal bancaria dispone de 3 cajeros automáticos. De vez en cuando el papel de algún cajero se atasca y el aparato deja de funcionar hasta que uno de los empleados (especialmente adiestrado para llevar a cabo esta tarea) consigue arreglar la avería. Se sabe que el tiempo que tarda dicho empleado en la reparación sigue una distribución exponencial con media 10 minutos, mientras que la distribución del tiempo que un cajero está funcionando hasta que se atasca el papel es también exponencial con media de 2 horas. Calcular:

La probabilidad de que funcionen los tres cajeros.
El número medio de cajeros averiados.
El tiempo medio que un cajero está averiado.
Si en un momento dado funcionan los tres cajeros, ¿cuál es el tiempo medio hasta la próxima avería?

Ejercicio A5.25. A una máquina perforadora de una cadena de producción llegan mecanismos de interruptores diferenciales según un proceso de Poisson, con tasa 10 por minuto. El tiempo, en minutos, necesario para llevar a cabo la perforación del mecanismo sigue una distribución exponencial con parámetro 12. Cuando un nuevo mecanismo llega a la máquina perforadora y sta está ocupada, aguarda según el turno que le corresponda, hasta que pueda ser perforado. A tal efecto, se supone que la zona de espera en la que se van almacenando los mecanismos antes de ser perforados es lo suficientemente amplia para que no existan aglomeraciones que sobrepasen estas dimensiones.

¿Cuál es el porcentaje de tiempo durante el cual la perforadora está libre?
¿Cuál es el número medio de mecanismos en toda la zona de perforación (perforadora y zona de espera)?
Calcular el tiempo medio que un mecanismo pasa en todo el proceso de perforación (desde que llega a esa zona hasta que sale perforado) y la probabilidad de que para un mecanismo se emplee más de un minuto en todo ese proceso.
Si ahora se supone que la zona de espera tiene sólo capacidad para 3 mecanismos y que cuando un mecanismo llega y se encuentra dicha zona completa, se desvía a otra rama de la cadena de producción, calcular la probabilidad de que se produzca dicho desvío.

Ejercicio A5.26. Un sistema informático de una biblioteca dispone de 3 lectores de códigos de barras para inventariar los nuevos libros. No obstante, de vez en cuando se produce algún error de lectura en alguno de ellos y deja de funcionar hasta que uno de los encargados de la biblioteca (que es quien siempre lleva a cabo esta tarea) consigue arreglar la avería. Se sabe que el tiempo que esta persona utiliza en dicha reparación sigue una distribución exponencial con media de 5 minutos, mientras que la distribución del tiempo que un lector está funcionando hasta que se produce algún error de lectura es también exponencial pero con media de 1 hora. Calcular:

La probabilidad de que funcionen los tres lectores.
El número medio de lectores averiados.
El tiempo medio que un lector está averiado.
Si en un momento dado funcionan dos lectores, ¿cuál es el tiempo medio hasta la próxima avería?

Ejercicio A5.27. Una factoría dispone de cuatro equipos de generación de corriente eléctrica que suministran gran parte de la energía que necesita dicha empresa. La distribución del tiempo que transcurre desde que un generador comienza a funcionar hasta que se avería es exponencial, con media de 40 días. El tiempo de reparación de un generador es una variable aleatoria de distribución exponencial y media 10 días. Sabiendo que existe un único técnico capaz de reparar los generadores, se pide:

La probabilidad de que el técnico esté ocupado.
El porcentaje medio de tiempo en el que todos los equipos de gene- ración están averiados.
El número medio de averías de equipos en un mes.
El tiempo medio que transcurre desde la avería de un equipo hasta su reparación.
El número medio de equipos funcionando.

Ejercicio A5.28. Una empresa de fabricación de puertas de madera tiene una unidad de negocio que fabrica puertas de muebles de cocina. Dichas puertas, de dimensiones diferentes según pedidos, reciben un tratamiento en 3 etapas. El número de puertas que la unidad de negocio fabrica es de alrededor de 50.000 puertas al año. La primera etapa consta de una única máquina que es capaz de procesar 220 puertas al día. La segunda etapa consta de dos máquinas que procesan cada una 140 puertas al día. La tercera etapa es una etapa manual, para la que se dispone de 3 trabajadores que tardan aproximadamente 5 minutos por puerta. Los días tienen 480 minutos y los años 240 días. Se pueden suponer tiempos distribuidos según una distribución exponencial tanto para las llegadas de pedidos como para los ritmos de producción.

¿Cuál es el número de puertas que habrá en cada etapa, en un instante cualquiera, incluyendo las puertas en las máquinas y las que están siendo procesadas por los operarios?
¿En que afectaría al sistema original que en la etapa segunda se colocara un limitador de capacidad, mediante el cual no se aceptaran en el almacén previo a dicha etapa más de 5 puertas?
Supón que en el sistema original la demanda de puertas asciende a 70000 puertas/año. Si se opta por mantener una sola máquina en la primera etapa, ¿cuántas horas extra al día debe trabajar dicha máquina? ¿En qué afectaría comprar una máquina más para esa etapa al cambio en los plazos de entrega? ¿Cómo se comportarían los almacenes?
Supón que en la segunda etapa, no hay dos si no tres máquinas. Dichas máquinas tardan en estropearse 3 días desde que se arreglan y un mecánico tarda de media 5 horas en arreglarlas cada vez. Sólo se dispone de un mecánico. ¿Tiene este sistema suficiente capacidad para hacer frente a la demanda?
Sobre el caso anterior, ¿qué porcentaje de tiempo sólo hay una máquina trabajando? ¿Y ninguna? ¿Qué ocurre con los almacenes durante el tiempo en que hay menos de dos máquinas trabajando?
Sobre el caso anterior, ¿qué opinión te merece que vaya uno de los trabajadores de la tercera sección a ayudar al mecánico cuando haya dos o más máquinas estropeadas en la sección 2, suponiendo que está formado como mecánico?
¿Cuál sería en el caso anterior la probabilidad de que hubiera más de una máquina estropeada?

Ejercicio A5.29. Una sección de una empresa fabrica puertas metálicas para ascensores. Las puertas para ascensores pueden tener una gran variedad de formatos, colores y huecos. Se puede admitir que el proceso de producción se compone de 4 etapas consecutivas. La empresa trabaja alrededor de 220 días al año. Cada día tiene 7 horas y 30 minutos de trabajo efectivo. Durante el pasado año se recibieron pedidos por un total de 8.500 puertas. Los pedidos varían bastante a lo largo del año, pero no parecen repercutir en los ritmos de producción promedio de las diferentes etapas de trabajo.

La primera etapa se realiza simultáneamente por dos equipos de trabajo, con un ritmo promedio cada uno de ellos de una puerta cada 20 minutos. La segunda etapa la realiza un equipo de trabajo con un tiempo de ciclo promedio de 11 minutos por puerta. La tercera etapa requiere del uso de otra máquina con un tiempo de ciclo promedio de 10 minutos por puerta. Por último la cuarta etapa es de preparación final. Como es un trabajo principalmente manual, que realiza un único operario, tiene un tiempo de ciclo de 18 minutos por unidad, y se dispone de tantos trabajadores como se requieran, pues irán viniendo de otras secciones siempre que haya una puerta por preparar. Asumiendo tiempos exponenciales:

¿Cuál será el número medio de puertas que habrá en el sistema?
¿Cuántos trabajadores serán necesarios normalmente en la cuarta etapa?
Si un pedido tiene 30 puertas ,¿cuánto tiempo tardará en promedio en ser servido?
¿Cuál es el tiempo promedio previsto de entrega de una puerta? ¿A qué puede ser debido y qué repercusiones tiene? Propón un mecanismo de corrección.
¿Cual será el efecto sobre la cantidad de puertas en la primera etapa si en lugar de dos equipos de trabajo con tiempos de ciclo como los citados se establece un único equipo más eficiente con un tiempo de ciclo de 9 minutos por unidad?

4 Cadenas de Markov de Tiempo Contínuo

6 Aplicaciones prácticas