Unidad 1 Conceptos básicos

En esta unidad repasamos los conceptos básicos de probabilidad relacionados con las variables aleatorias y las distribuciones de probabilidad. Presentamos las distribuciones de probabilidad más relevantes, discretas y continuas, y otras no estandarizadas, junto con varios algoritmos y funciones de R útiles para simularlas y realizar cálculos de probabilidad. Resolvemos por simulación múltiples problemas basados en los diferentes tipos de variables presentadas. Por último, introducimos la definición de proceso estocástico, con diversos ejemplos, con el fin de preparar el camino para las unidades siguientes, que ya estarán enfocadas en estudiar en profundidad diferentes tipos de procesos estocásticos. Proponemos al final de la unidad más ejercicios y estudios de caso, para que el alumnado practique los conceptos y algoritmos estudiados.

1.1 Variables aleatorias

Introducimos una serie de conceptos básicos.

Definición 1.1 Una variable aleatoria es una función que asigna un número real a cada uno de los posibles resultados de un experimento o característica de interés susceptibles de ser observados o medidos en una población objetivo.

Las variables aleatorias pueden ser discretas o continuas en función de sus posibles valores. Si los valores o resultados posibles se pueden contar (sin ser infinitos), se dice que la variable aleatoria es ‘discreta’; en caso contrario, se dice que es ‘continua.’ Veamos varios ejemplos.

Ejemplo 1.1 Un proveedor vende huevos por cajas que contienen 144 huevos. El proveedor desea estudiar el número de huevos que se suelen romper en cada una de las cajas durante el proceso de distribución. Es de interés pues, la variable aleatoria $N$ que contabiliza el número de huevos rotos en una caja, y cuyos valores posibles son $0, 1, 2,..., 144$. Se trata por tanto de una variable de tipo discreto.

Ejemplo 1.2 Se desea realizar un estudio para estimar la estatura de los habitantes de una ciudad. Se define la variable aleatoria $X$ como la altura en cm de cada uno de los habitantes de la ciudad. Dado que los posibles resultados son infinitos, diremos que dicha variable es de tipo continuo.

Definición 1.2 Se define el espacio probabilístico $S$ asociado a una variable aleatoria como el conjunto de todos los valores posibles o con probabilidad que puede tomar dicha variable.

1.1.1 Función de probabilidad

Para caracterizar completamente cualquier variable aleatoria es necesario definir la función de distribución, que nos da la probabilidad acumulada por debajo de un valor plausible en el espacio probabilístico $S$ en el que está definida dicha variable.

Definición 1.3 La función de distribución para una variable $X$ en un punto $a$ del espacio probabilístico $S$ se define como la probabilidad acumulada por debajo de dicho valor:

\[\begin{equation*} F(a) = P(X \leq a). \end{equation*}\]

En el caso de variables aleatorias de tipo discreto podemos caracterizar su comportamiento mediante las probabilidades asociadas a cada uno de los elementos del espacio probabilístico Esto se hace a través de la ‘función puntual de probabilidad’ o ‘función de masa de probabilidad.’

Definición 1.4 La función de masa de probabilidad (fmp) para una variable discreta $X$ en un punto $a$ del espacio probabilístico $S$ se define como la probabilidad de que la variable $X$ tome dicho valor:

\[\begin{equation*} f(a) = P(X = a). \end{equation*}\]

En el caso de variables aleatorias de tipo discreto, la función de distribución de probabilidad se puede obtener a partir de la función de masa de probabilidad como:

\[\begin{equation*} F(a) = \sum_{k \leq a} f(k) = 1 - \sum_{k > a} f(k). \end{equation*}\]

para cualquier valor de $a$ en $S$.

Sim embargo, en las variables aleatorias de tipo continuo no es posible asignar una probabilidad a cada uno de los infinitos valores de la variable, dado que en ese caso la probabilidad del espacio probabilístico íntegro excedería el valor 1 y por lo tanto no sería una probabilidad. En estas variables es preciso definir otra función que permita cuantificar cualquier situación que involucre los resultados del espacio probabilístico $S$ asociado a la variable aleatoria. Surge la ‘función de densidad de probabilidad.’

Definición 1.5 La función de densidad de probabilidad (fdp), $f$, asociada a una variable $X$ de tipo continuo permite calcular la probabilidad acumulada en un intervalo cualesquiera $(a,b]$ del espacio probabilístico $S$ a través de la integral en dicho intervalo:

\[\begin{equation*} \int_{a}^{b} f(s)ds = Pr(a < X \leq b) = F(b) - F(a). \end{equation*}\]

De esta forma la ‘función de distribución’ de una variable continua se puede obtener como:

\[\begin{equation*} F(a) = \int_{r_{min}}^{a} f(s)ds. \end{equation*}\]

donde $r_{min}$ es el valor mínimo de $X$ en el espacio probabilístico $S$.

1.1.2 Variables relevantes

Hay muchas funciones de distribución que se utilizan con tanta frecuencia que se conocen con nombres especiales, y que presentamos en las Secciones Distribuciones Discretas y Distribuciones continuas. Para estas variables resulta bastante sencillo realizar cualquier calculo de probabilidad, ya que la mayoría de programas informáticos tienen implementadas sus funciones de distribución. Utilizaremos no obstante la simulación para realizar cálculos probabilísticos.

En $R$ se puede acceder directamente a la función de densidad, función de distribución, quantiles y simulación de valores de cualquiera de las distribuciones que presentamos a continuación mediante las funciones:

$dXXXX(par)$: función de densidad,
$pXXXX(par)$: función de distribución,
$qXXXX(par)$: quantiles,
$rXXXX(par)$: generación de valores de la variable,

donde $XXXX$ identifica la distribución/variable de interés y $par$ son los parámetros que la caracterizan.

1.1.3 Media y varianza

Muchas variables aleatorias tienen funciones de distribución complicadas y, por tanto, es difícil obtener una comprensión intuitiva del comportamiento de la variable conociendo simplemente la función de distribución. Dos medidas, la media o valor esperado y la varianza se definen para ayudar a describir el comportamiento de una variable aleatoria. El valor esperado equivale a la media aritmética de infinitas observaciones de la variable aleatoria y la varianza es una indicación de la variabilidad o dispersión de los valores de dicha variable.

Definición 1.6 Dada una variable aleatoria $X$ discreta sobre un espacio probabilístico $S$, se define el valor esperado o esperanza de $X$, $E(X)$, como

\[E(X) = \sum_{k \ in S} kf(k)\]

donde $f$ es la fmp de $X$.

Cuando $X$ es una variable aleatoria continua, su valor esperado se define a partir de la fdp de $X$:

\[E(X) = \int_S xf(x)dx.\]

Esta definición se puede aplicar a cualquier función o transformación de una variable aleatoria, $h(X)$, para obtener su valor esperado $E[h(X)]$, y así por ejemplo en el caso continuo tendríamos:

\[E[h(X)]=\int_S h(x)f(x)dx.\]

El valor esperado nos da una medida de localización para la variable aleatoria $X$, pero es bien sabido que dichas medidas de localización se deben acompañar siempre de una medida de dispersión, como la varianza o desviación típica.

Definición 1.7 Dada una variable aleatoria $X$ con valor esperado $E(X)$ se define la varianza de $X$, $V(X)$ como:

\[V(X) = E[(X-E(X))^2]=E(X^2) - E(X)^2\]

A partir de la varianza se define la desviación típica de la variable $X$ como la raíz cuadrada de su varianza. Las propiedades siguientes se derivan directamente a partir de la definición de esperanza y varianza:

Si $X$ e $Y$ son dos variables aleatorias y $c$ una constante, entonces:

$E(c) = c$
$E(cX) = cE(X)$
$E(X+Y) = E(X) + E(Y)$
$V(cX) = c^2 V(X)$

1.2 Aproximación Monte Carlo

Cuando trabajamos con variables aleatorias, es común el problema de querer estimar el valor esperado de cualquier cantidad $h(X)$, siendo $X$ una variable aleatoria. Utilizando la simulación es posible obtener estimaciones de dichos valores de un modo relativamente sencillo: a través de la integración Monte Carlo.

Ante un problema genérico relativo a calcular el valor esperado de cierta función $h(X)$ para una variable aleatoria con fdp $X \sim f(x)$,

\[\begin{equation} E[h(X)]=\int_S h(x) f(x) dx \tag{1.1} \end{equation}\]

donde $S$ denota el conjunto en el que la variable $X$ toma valores,

Definición 1.8 Ante el problema de estimar (1.1), el procedimiento de estimación Monte Carlo propone simular una muestra aleatoria de la distribución de $X$, $x_1,\ldots,x_n$ y con ella obtener una aproximación empírica a través del promedio de las cantidades $h(x_1),\ldots,h(x_n)$,

\[\begin{equation} \bar{h_n}=\frac{\sum_{i=1}^n h(x_i)}{n}. \tag{1.2} \end{equation}\]

Por la Ley de los Grandes Números, $\bar{h_n}$ converge casi seguro a la cantidad de interés $E[h(X)]$. Además, cuando $h^2(X)$ tiene un valor esperado finito, la velocidad de convergencia de $\bar{h_n}$ se puede calcular y la varianza asintótica de la aproximación es \[Var(\bar{h_n})=\frac{1}{n} \int_S (h(x)-E[h(X)])^2 f(x) dx,\] que se puede estimar con la muestra $x_1,\ldots,x_n$ a través de

\[\begin{equation} v_n=\frac{1}{n^2} \sum_{i=1}^n [h(x_i)-\bar{h_n}]^2. \tag{1.3} \end{equation}\]

Más específicamente, por el Teorema Central del Límite, para $n$ grande tendremos que

\[\begin{equation} \frac{\bar{h_n}-E[h(X)]}{\sqrt{v_n}} \sim N(0,1), \tag{1.4} \end{equation}\]

lo que permitirá además, construir bandas de confianza para la aproximación Monte Carlo, a la que en adelante nos referiremos por “aproximación MC.”

\[\begin{equation} IC_{1-\alpha}[\bar{h_n}]=[\bar{h_n}-z_{1-\alpha/2} \sqrt{v_n}, \bar{h_n}+z_{1-\alpha/2} \sqrt{v_n}] \tag{1.5} \end{equation}\]

donde $z_{1-\alpha/2}$ es el cuantil $1-\alpha/2$ de una normal estándar, asociado al nivel de confianza $1-\alpha$.

1.2.1 MC y probabilidad

Aunque en las situaciones más sencillas se puede evaluar cualquier probabilidad mediante la correspondiente función de distribución, en muchas ocasiones resulta sencillo obtener una muestra simulada de la variable aleatoria y aproximar dicha probabilidad de interés mediante el denominado estimador Monte-Carlo.

Se obtiene la estimación Monte-Carlo (MC) de la probabilidad de que una variable aleatoria $X$ tome algún valor en un conjunto $A$ de valores dentro de su espacio probabilístico, $Pr(X \in A)$, a partir de un conjunto de observaciones o simulaciones $x_1, x_2,...,x_N$ de la variable $X$, mediante el cociente entre el número de simulaciones que están en dicha región $A$, y el número de datos disponibles,

\[\begin{equation} Pr(X \in A) \approx \frac{\#\{x_1, x_2,...,x_N\} \in A}{N}. \end{equation}\]

Básicamente esta definición se fundamenta en la interpretación empírica de la probabilidad, a través del ratio de casos favorables por casos posibles:

\[probabilidad=\frac{\mbox{casos favorables}}{\mbox{casos posibles}}.\]

La fórmula anterior la podemos expresar en notación similar a la utilizada en (1.2) definiendo una variable dicotómica \[I_A(X)=1 \text{, si } X \in A\] y 0 en otro caso, de manera que el problema de calcular una probabilidad según una distribución de probabilidad para $X$ se convierte en el valor esperado de una distribución Bernouilli para una distribución de

\[Pr(X \in A)=\int_A f(x)dx=\int_S I_A(X)f(x)dx=E[I_A(X)]\] y la estimación MC (1.2) se puede expresar, para un conjunto de $n$ simulaciones $x_1,\ldots,x_n$, como

\[\begin{equation} Pr(X \in A)\approx \hat{h_n}= \frac{\sum_{i=1}^n I_A(x_i)}{n}, \tag{1.6} \end{equation}\]

y su varianza con

\[\begin{equation} v_n=\frac{1}{n^2} \sum_{i=1}^n [I_A(x_i)-\bar{h_n}]^2. \tag{1.7} \end{equation}\]

Ejemplo 1.3 En la situación del ejemplo 1.1, supongamos que disponemos de un conjunto de 200 simulaciones del número de huevos defectuosos en 200 cajas distribuídas. Queremos descubrir, utilizando exclusivamente esas simulaciones:

La probabilidad de que una caja tenga más de 3 huevos defectuosos, $Pr(X>3)$.
La probabilidad de que una caja tenga a lo sumo 3 huevos defectuosos, $Pr(X\leq 3)$.
La probabilidad de que una caja no tenga ningún huevo defectuoso, $Pr(X=0)$.
La probabilidad de que la proporción de huevos defectuosos en una caja sea inferior al 1%, $Pr(X/144 < 0.01)=Pr(X<1.44)$.

# Simulaciones disponibles
defectos <- c(2, 2, 0, 0, 0, 2, 1, 2, 1, 4, 1, 0, 0, 2, 4, 
0, 0, 0, 0, 1, 1, 1, 2, 2, 3, 1, 0, 4, 3, 1, 0, 
2, 2, 2, 3, 1, 0, 2, 2, 2, 3, 1, 0, 1, 0, 1, 2, 
0, 0, 2, 3, 2, 3, 2, 4, 4, 0, 1, 1, 3, 0, 0, 3, 
2, 0, 0, 0, 3, 0, 1, 4, 1, 1, 2, 1, 1, 4, 1, 1, 
1, 0, 1, 0, 1, 2, 2, 1, 3, 1, 2, 1, 2, 3, 1, 2, 
5, 1, 1, 1, 1, 0, 1, 1, 1, 2, 1, 0, 0, 1, 2, 2, 
1, 1, 1, 1, 0, 3, 1, 1, 1, 1, 4, 4, 0, 6, 6, 1, 
1, 1, 0, 2, 3, 1, 0, 0, 2, 0, 2, 1, 1, 1, 2, 1, 
1, 1, 1, 2, 5, 0, 1, 3, 1, 1, 4, 1, 2, 1, 1, 0, 
2, 1, 2, 1, 3, 3, 2, 0, 3, 0, 1, 3, 0, 1, 2, 0, 
1, 0, 0, 2, 2, 1, 2, 0, 0, 0, 1, 1, 2, 3, 1, 0, 
1, 0, 1, 1, 1, 1, 1, 5, 3)
# Número de simulaciones/observaciones
nsim=length(defectos)
# Tamaño de la caja
tamaño <- rep(144,200)
# Conjunto de datos
huevos <- data.frame(tamaño, defectos)

Y vamos aproximando por Monte-Carlo las probabilidades de interés, estableciendo las condiciones lógicas en cada situación.

# Pr(X > 3)
sel <- dplyr::filter(huevos, defectos >3)
prob <- nrow(sel)/nsim
cat("Probabilidad estimada [Pr(X > 3)]: ", prob)

## Probabilidad estimada [Pr(X > 3)]:  0.075

# Pr(X <= 3)
sel <- dplyr::filter(huevos, defectos <= 3)
prob <- nrow(sel)/nsim
cat("Probabilidad estimada [Pr(X <= 3)]: ", prob)

## Probabilidad estimada [Pr(X <= 3)]:  0.925

# Pr(X = 0)
sel <- dplyr::filter(huevos, defectos == 0)
prob <- nrow(sel)/nsim
cat("Probabilidad estimada [Pr(X = 0): ", prob)

## Probabilidad estimada [Pr(X = 0):  0.235

# Pr(X/144 <=0.01)
sel <- dplyr::filter(huevos, defectos <= (0.01*144))
prob <- nrow(sel)/nsim
cat("Probabilidad estimada [Pr(X/144 <=0.01): ", prob)

## Probabilidad estimada [Pr(X/144 <=0.01):  0.62

El error asociado a la estimación de la probabilidad anterior, lo calculamos aplicando (1.7), y también el intervalo de confianza al 95% con (1.5).

I.a=(huevos$defectos <= 1.44)*1
prob=mean(I.a)
cat("prob.estim=",prob)

## prob.estim= 0.62

vn=sum((I.a-prob)^2)/(nsim^2)
error=sqrt(vn)
cat("Error Estimado=",round(error,3))

## Error Estimado= 0.034

# límites del IC redondeados a 3 cifras decimales
ic.low=round(prob-qnorm(0.975)*error,3)
ic.up=round(prob+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC(prob.estim)]=[",ic.low,",",ic.up,"]")

## IC(95%)[AproxMC(prob.estim)]=[ 0.553 , 0.687 ]

De esta forma resultará posible estimar cualquier probabilidad asociada a una variable aleatoria, aun desconociendo su función de distribución o de probabilidad, siempre que dispongamos de una muestra simulada, y esta estimación será más precisa cuanto mayor sea el tamaño de dicha muestra.

1.2.2 MC y momentos

Si disponemos de una muestra (de observaciones o simulaciones) lo suficientemente grande de la variable aleatoria $X$ podemos aproximar -de modo razonablemente preciso- el valor esperado y la varianza (o desviación típica) sin más que calcular la media y varianza de los datos que componen la muestra.

La precisión de estas estimaciones estará directamente relacionada con el tamaño de la muestra utilizada.

Sean $x_1, x_2,...,x_N$ simulaciones disponibles para $X$. Entonces

\[\begin{eqnarray*} E(X) &\approx& \bar{x}_N=\sum_{i=1}^N x_i /N \\ Var(X) &\approx& \sum_{i=1}^N (x_i-\bar{x}_N)^2/n = \bar{x}_N^2-\sum_{i=1}^N x_i^2 /N. \end{eqnarray*}\]

Ejemplo 1.4 Con los datos del ejemplo anterior, queremos saber cuál es el número aproximado de huevos que se rompen en cada caja, conocer su dispersión y tener así mismo un intervalo de confianza para la media.

# media
media=mean(huevos$defectos)
# dispersión
varianza=var(huevos$defectos)
desvtip=sd(huevos$defectos)

# ic para la media
error=sqrt(sum((huevos$defectos-media)^2)/(nsim^2))
cat("\n Error Estimado (media)=",round(error,3))

## 
##  Error Estimado (media)= 0.089

# límites del IC redondeados a 3 cifras decimales
ic.low=round(media-qnorm(0.975)*error,3)
ic.up=round(media+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC(media)]=[",ic.low,",",ic.up,"]")

## IC(95%)[AproxMC(media)]=[ 1.255 , 1.605 ]

1.3 Distribuciones discretas

Destacamos como principales variables de tipo discreto las siguientes: Bernouilli, Binomial, Geométrica y Poisson.

1.3.1 Bernouilli

Imaginemos una situación experimental donde el resultado de cierta variable que observamos únicamente puede tomar dos valores posibles, denominados “éxito” (codificado con el valor 1) y “fracaso” (codificado con el valor 0). Así pues, la variable aleatoria asociada $X$ verifica que:

\[\begin{equation} Pr(X = x) = \begin{cases} \theta & \text{ si } x = 1 (\text{ éxito})\\ 1- \theta & \text{ si } x = 0 (\text{ fracaso.}) \end{cases} \tag{1.8} \end{equation}\]

Definición 1.9 Una variable aleatoria $X$ cuya fmp viene dada por (1.8) se denomina variable Bernouilli, con probabilidad de éxito $\theta$, y se denota por:

\[X \sim Ber(\theta)\]

de forma que $E(X) = \theta$ y $V(X) = \theta(1-\theta).$

Un ejemplo típico de una variable Bernouilli es el lanzamiento de una moneda que sólo tiene dos posibles resultados: cara o cruz. Si la moneda esta equilibrada tenemos que $\theta = 0.5$ (idéntica probabilidad para cualquiera de los dos resultados), de forma que si definimos por ejemplo el éxito por conseguir cara, tendremos:

\[X = \text{ Obtener cara } \sim Ber(0.5)\]

Una distribución $Ber(p)$ es equivalente a una distribución binomial con parámetros 1 y p, $Bin(1,p)$, de modo que para simular y realizar cálculos de probabilidad con ella utilizaremos las funciones correspondientes a la distribución binomial que vemos a continuación.

La función dbinom(x,1,prob) nos permite evaluar la $Pr(X=x)$ para una variable Bernoilli con probabilidad de éxito prob.
La función pbinom(x,1,prob) nos permite evaluar la $Pr(X \leq x), x=0,1$.
La función rbinom(n,1,prob) permite simular $n$ valores Bernouilli.

1.3.2 Binomial

Consideramos un experimento Bernouilli que repetimos en $n$ ocasiones, obteniendo en cada repetición sólo dos resultados posibles, “éxito” o “fracaso,” con cierta probabilidad $\theta$ para el éxito, y contabilizamos el número de éxitos $N$. Los posibles resultados de este experimento son $\{0, 1, 2,...,n\}$ éxitos conseguidos en un total de $n$ pruebas. La probabilidad de observar $x$ éxitos en $n$ pruebas viene dada por la función:

\[\begin{equation} Pr(N = x) = \frac{n!}{x!(n-x)!} \theta^{x} (1-\theta)^{n-x} \text{ para } x = 0, 1,\ldots,n, \tag{1.9} \end{equation}\]

con $n$ el número de repeticiones o pruebas Bernouilli realizadas, $x$ el número de éxitos obtenidos, y $\theta$ la probabilidad de éxito.

Definición 1.10 La variable aleatoria $N$ que se obtiene como la suma de $n$ variables Bernouilli independientes con la misma probabilidad de éxito $\theta$, y cuya función de masa de probabilidad viene dada en (1.9), se denomina variable Binomial de tamaño $n$ y probabilidad de éxito $\theta$, y se denota por:

\[N \sim Bi(n,\theta)\]

con $E(N) = n\theta$ y $V(N) = n\theta(1-\theta).$

A continuación se presentan algunos ejemplos de aplicación de la variable Binomial donde representamos tanto la fmp como la función de distribución asociada al problema de interés. Antes mencionamos las funciones de R relacionadas con esta distribución.

La función dbinom(x,size,prob) nos permite evaluar la $Pr(N=x)$ para una variable Binomial con tamaño size y probabilidad de éxito prob.
pbinom(x,size,prob) permite evaluar la $Pr(N \leq x)$.
rbinom(n,size,prob) permite simular $n$ valores de una variable Binomial de tamaño size y probabilidad de éxito $prob$.

Ejemplo 1.5 Estamos revisando en una empresa el comportamiento de las bajas laborales. En base al histórico, se tiene que cada día aproximadamente el 3% de los trabajadores faltan al trabajo alegando una baja laboral. Si el número de trabajadores de la empresa es de 150, queremos saber qué porcentaje de días vamos a tener al menos 3 trabajadores de baja.

Denotemos por $N$ a la variable aleatoria que indica el número de trabajadores de baja en un día cualquiera, e identifiquemos el “éxito” por el hecho de “estar de baja.” Así, podemos asumir que la distribución de $N$ es binomial, con tamaño 50 y probabilidad 0.03.

\[N \sim Bi(50,0.03).\]

En consecuencia, el valor esperado del número de trabajadores de baja cada día es $E(N) = 50 \cdot 0.03=1.5$.

A continuación, en la Figura 1.1 representamos la fmp y la función de distribución asociadas.

# los valores posibles de la variable Bin(1000,0.03) son
xs <- 0:50
n=50
p=0.03
# Data frame
datos <- data.frame(xs = xs, probs = dbinom(xs, n,p), 
                    probsacum = pbinom(xs, n,p))
# función de masa de probabilidad
g1 <- ggplot(datos, aes(x=xs, y=probs)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  ylim(0,0.5) +
  labs(x ="x", y = "Probabilidad puntual. Pr(N=x)")
# función de distribución
g2 <- ggplot(datos, aes(xs, probsacum)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  labs(x ="x", y ="Probabilidad acumulada. Pr(N<=x)")
grid.arrange(g1, g2, nrow = 1)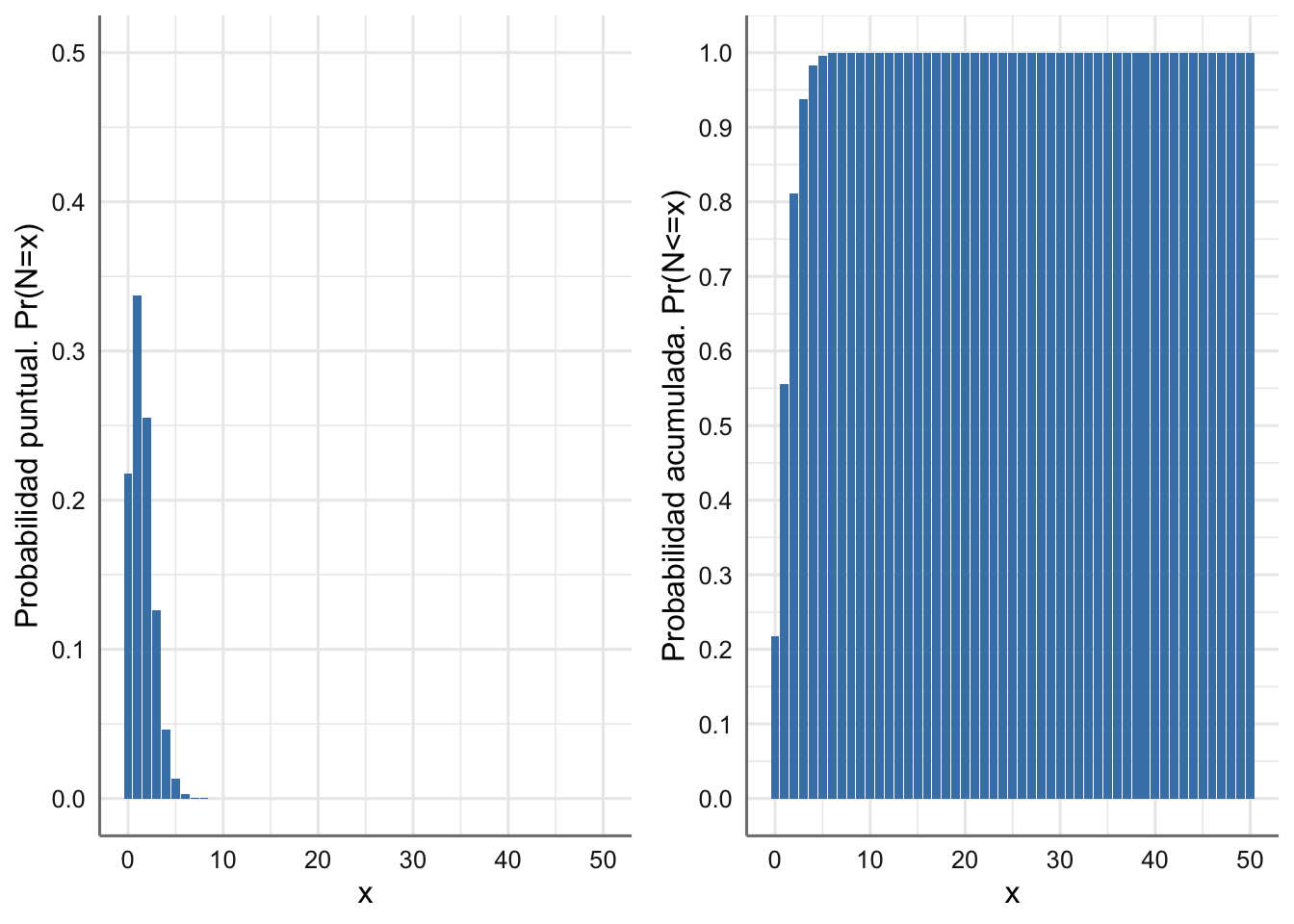

Figura 1.1: Función de masa de probabilidad y Función de distribución para el número de trabajadores de baja un día cualquiera.

En la fmp (Figura 1.1-izquierda) podemos ver que en este caso la probabilidad se concentra en muy pocos valores, en concreto por debajo de 10, de modo que antes de llegar a $x=10$ la probabilidad acumulada llega al valor 1, como se aprecia en la Figura 1.1-derecha.

La probabilidad que nos reclaman en el enunciado es \[Pr(N\geq 3)=1-Pr(N \leq 2),\] que calculamos y podemos aproximar por MC a partir, por ejemplo, de 1000 simulaciones.

nsim=1000
n=50
p=0.03
# valor real de la probabilidad
prob=1-pbinom(2,n,p)
cat("Pr(N>=3)=",round(prob,3))

## Pr(N>=3)= 0.189

set.seed(1234)
# simulaciones
I.a=(rbinom(nsim,n,p)>=3)*1  # función indicatriz para la probabilidad requerida
prob=mean(I.a)
cat("AproxMC=",prob)

## AproxMC= 0.193

El error estimado de esta aproximación, que calculamos con la raíz cuadrada de (1.3) es

error=sqrt(sum((I.a-prob)^2)/(nsim^2))
cat("Error.AproxMC=",round(error,3))

## Error.AproxMC= 0.012

de donde podríamos calcular un intervalo de confianza para la aproximación MC de $Pr(N \geq 3)$ al 95% utilizando la distribución (1.4) y la fórmula (1.5):

# límites del IC redondeados a 3 cifras decimales
ic.low=round(prob-qnorm(0.975)*error,3)
ic.up=round(prob+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")

## IC(95%)[AproxMC]=[ 0.169 , 0.217 ]

Ejemplo 1.6 Una empresa de fabricación produce piezas, de las cuales el 97% están dentro de las especiﬁcaciones y el 3% son defectuosas (fuera de las especiﬁcaciones). Aparentemente no hay ningún patrón en la producción de piezas defectuosas. La cadena de producción empaqueta las piezas en cajas de 20 piezas cada una, y produce 1000 cajas al día. Al gerente de la empresa le gustaría estimar el número de cajas con al menos dos piezas defectuosas, de entre todas las que se producen al día durante un día cualquiera.

Si $N$ es la variable aleatoria que recoge el número de piezas defectuosas en una caja, tenemos que:

\[N \sim Bi(20, 0.03)\]

La probabilidad de que una caja tenga al menos dos piezas defectuosas se calcula con $p_N=Pr(N \geq 2)=1-Pr(N\leq 1)$.

n=20
p=0.03
prob=(1 - pbinom(1, n,p))
cat("Probabilidad de que una caja tenga al menos dos defectos=",prob)

## Probabilidad de que una caja tenga al menos dos defectos= 0.119838

Sin embargo, lo que nos piden es, de un total de 1000 cajas, cuál es el número esperado de cajas con al meos dos piezas defectuosas. Para ello, surge la variable $D_N$ que representa el número de cajas, de un total de 1000, con al menos 2 piezas defectuosas, que es binomial de tamaño 1000 y probabilidad $p_N$,

\[D_N \sim Bin(1000,p_N),\]

y lo que nos están pidiendo es $E(D_N)=1000 p_N$.

Si simulamos con la distribución de $N$ lo acontecido un día, esto es, con 1000 cajas o simulaciones, y contamos el número de cajas con 2 o más piezas defectuosas, obtenemos una aproximación a la cantidad que nos piden.

n=20
p=0.03
sum(rbinom(1000,n,p)>=2)

## [1] 99

El problema es que no todos los días son iguales. De hecho si repites los siguientes cálculos varias veces, verás como el resultado varía. La aproximación Monte Carlo habría de considerar simulaciones de la variable $D_n$ , esto es, nsim días, para con ellos poder sacar una conclusión “promedio” de lo que puede ocurrir un día cualquiera.

nsim=5000 # número de días simulados
n=1000
p=prob
# valor real del valor esperado
media=n*p
cat("E(D_N)=",round(media,3))

## E(D_N)= 119.838

# simulaciones
xi=rbinom(nsim,n,p)
m=mean(rbinom(nsim,n,p))
cat("AproxMC=",m)

## AproxMC= 119.7926

# Error MC
error=sqrt(sum((xi-m)^2)/(nsim^2))
# límites del IC redondeados a 3 cifras decimales
ic.low=round(m-qnorm(0.975)*error,3)
ic.up=round(m+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")

## IC(95%)[AproxMC]=[ 119.51 , 120.076 ]

1.3.3 Geométrica

Imaginemos una situación experimental donde se repite un experimento hasta que sucede un “éxito.” En otras palabras, se piensa en $\theta$ como la probabilidad de éxito para un solo ensayo, y realizamos sucesivamente los ensayos hasta que se produce un éxito. La variable aleatoria $N$ se define entonces como el número de ensayos Bernouilli realizados hasta conseguir un éxito. Nótese que aunque la variable aleatoria geométrica es discreta, su rango es inﬁnito, y su fmp viene dada por:

\[\begin{equation} Pr(N = x) = \theta (1-\theta)^{x} \text{ para } x = \text{1, 2,...} \tag{1.10} \end{equation}\]

con $x$ el número de repeticiones hasta alcanzar un éxito, y $\theta$ la probabilidad de éxito.

Definición 1.11 La variable aleatoria $N$ cuya función de masa de probabilidad viene dada en (1.10) se denomina variable Geométrica de parámetro $\theta$, y se denota por:

\[N \sim Ge(\theta)\]

con $E(N) = \frac{1 - \theta}{\theta}$ y $V(N) = \frac{1-\theta}{\theta^2}.$

Las funciones de R relacionadas con esta distribución se presentan a continuación, y tras ello un ejemplo de aplicación de la variable Geométrica.

La función dgeom(x, prob) nos permite evaluar la $Pr(N=x)$ para una variable Geométrica con probabilidad de éxito prob.
pgeom(x, prob) calcula la función de distribución.
rgeom(n, prob) permite generar $n$ valores de una variable Geométrica con probabilidad de éxito $prob$. Los resultados que proporciona son el número de repeticiones realizadas hasta alcanzar el primer éxito.

Ejemplo 1.7 Una vendedora de coches ha hecho un análisis estadístico de su historial de ventas anterior y ha determinado que cada día tiene un 10% de probabilidad de vender un coche de lujo. Tras un cuidadoso análisis posterior, también está claro que la venta de un coche de lujo en un día es independiente de la ventas realizadas cualquier otro día. El día de Año Nuevo (un día festivo en el que el concesionario estaba cerrado) la vendedora está intentando predecir cuándo venderá su primer coche de lujo del año.

Si consideramos $N$ como la variable aleatoria que indica el día de la primera venta de coches de lujo (N = 1 implica que la venta se realizaría el día 2 de enero), entonces:

\[N \sim Ge(0.1)\]

En este caso el valor esperado del número de días transcurridos hasta la venta del primer coche de lujo es $E(N) = 0.9/0.1 = 9$ días, con una desviación típica de 9.5 días. Así pues, es posible que el día 10 de enero tenga su primera venta. En la Figura 1.2 se muestran la fmp y la función de distribución asociadas.

# Valores de N
xs <- seq(0, 60, 1)
# Data frame
datos <- data.frame(xs = xs, probs = dgeom(xs, 0.1), 
                    probsacum = pgeom(xs, 0.1))
# función de masa de probabilidad
g1 <- ggplot(datos, aes(xs, probs)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  ylim(0,0.12) +
  labs(x ="x", y = "Probabilidad puntual. Pr(N=x)")
# función de distribución
g2 <- ggplot(datos, aes(xs, probsacum)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  labs(x ="x", y = "Probabilidad acumulada Pr(N<=x)")
grid.arrange(g1, g2, nrow = 1)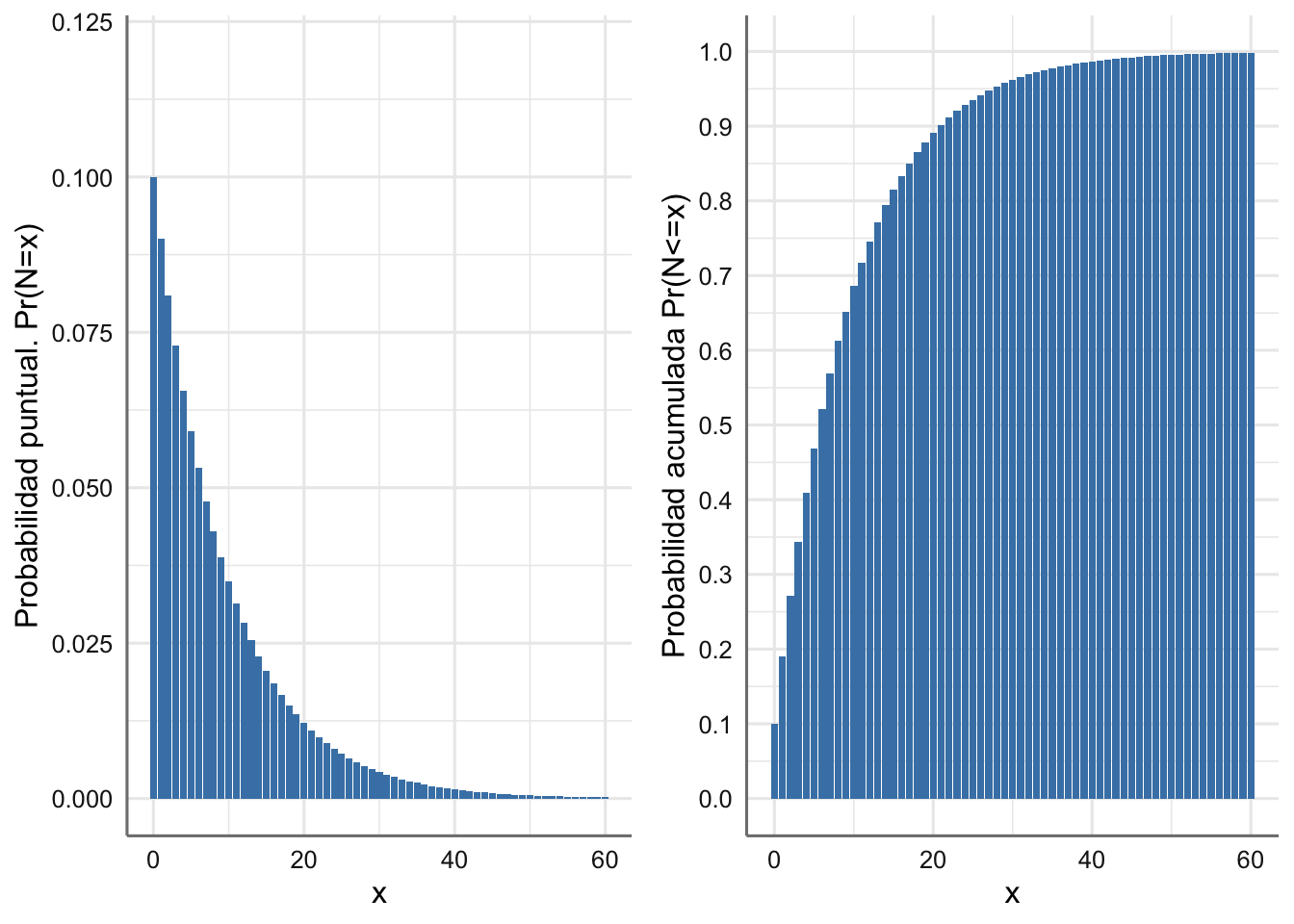

Figura 1.2: Función de masa de probabilidad y Función de distribución para el día en que venderá el primer coche de lujo.

Hacemos a continuación un análisis de simulación para aproximar los datos teóricos dados en la definición 1.11. Simulamos 1000 valores de una $Ge(0.1)$, con los que calculamos una aproximación al valor esperado de los días que deben transcurrir para vender un coche de lujo, y construimos un intervalo de confianza para la aproximación MC según (1.5).

# Parámetros de la simulación

set.seed(1970)
nsim <- 10000
prob <- 0.1
media<-(1-prob)/prob
cat("E(N)=",media)

## E(N)= 9

# Valores simulados
datos <- rgeom(nsim, prob)
# Aproximación MC del valor esperado
m=round(mean(datos),0)
cat("AproxMC=",m)

## AproxMC= 9

# Error MC
error=sqrt(sum((datos-m)^2)/(nsim^2))
# límites del IC redondeados a 3 cifras decimales
ic.low=round(m-qnorm(0.975)*error,3)
ic.up=round(m+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")

## IC(95%)[AproxMC]=[ 8.811 , 9.189 ]

1.3.4 Poisson

La distribución de Poisson se emplea como un modelo para variables aleatorias de tipo discreto cuando se quieren obtener las probabilidades de ocurrencia de un evento que se distribuye al azar en el espacio o el tiempo. Algunos ejemplos de esta distribución se presentan a continuación.

En el estudio de cierto organismo acuático, se toman un gran número de muestras de un lago y se cuenta el número de dichos organismos que aparecen en cada muestra. Podríamos plantear como objetivo el conocer cuál es la probabilidad de encontrar dicho organismo en una próxima muestra si la media observada en el conjunto de muestras es de 2 organismos.
En un estudio sobre la efectividad de un insecticida sobre cierto tipo de insecto, se fumiga una gran región. Posteriormente se crea una cuadrícula sobre el terreno, se selecciona de forma aleatoria un conjunto de ellas, y se cuenta el número de insectos vivos dentro de cada una. Planteamos como objetivo conocer cuál es la probabilidad de que no encontremos ningún insecto vivo en una próxima cuadrícula si se sabe que la media de insectos vivos en las cuadrículas analizadas es de 0.5.
Un grupo de investigadores observó la ocurrencia de hemangioma capilar retiniano (RCH) en pacientes con la enfermedad de von Hippel-Lindau (VHL). RCH es un tumor vascular benigno de la retina. Usando una revisión retrospectiva de series de casos consecutivos, los investigadores encontraron que el número de medio de tumores RCH por ojo para pacientes con VHL era de 4. Están interesados en conocer cuál es la probabilidad de que se detecten más de cuatro tumores por ojo.

La variable aleatoria $N$ se define entonces como el número de eventos que ocurren en un espacio o un tiempo determinados, y viene caracterizada por la denominada tasa de eventos o número medio de eventos que ocurren en el tiempo o espacio, y que se denota habitualmente por $\lambda$. El rango de esta variable es infinito y su fmp viene dada por:

\[\begin{equation} Pr(N = x) = \frac{e^{-\lambda}\lambda^x}{x!} \text{ para } x = \text{1, 2,...} \tag{1.11} \end{equation}\]

con $\lambda$ es la tasa y $x$ es el número de eventos que han ocurrido.

Definición 1.12 La variable aleatoria $X$ cuya función de masa de probabilidad viene dada en (1.11) se denomina variable poisson de parámetro $\lambda > 0$, y se denota por:

\[N \sim Po(\lambda)\]

con $E(N) = \lambda$ y $V(N) = \lambda.$

A continuación vemos diferentes ejemplos de uso de la distribución de Poisson, tras presentar las funciones de R relacionadas.

La función dpois(x, lambda) nos permite evaluar la $Pr(X=x)$ para una variable poisson de media $\lambda$.
ppois(x, lambda) calcula la función de distribución.
rpois(n, lambda) permite generar $n$ valores de una variable Poisson con media $\lambda$. Los resultados que proporciona son el número de eventos que ocurren en el tiempo o espacio determinado.

Ejemplo 1.8 Una empresa de asesoramiento está realizando el análisis del funcionamiento de una panadería y ha estimado que el número medio de barras de pan que se venden en un periodo de media hora es de 12. La empresa está interesada en saber cuál es la capacidad de venta en cada franja de diez minutos (pues es prácticamente el tiempo de horneado), y también cuál es la probabilidad de que el número de barras que se venden en diez minutos sea exactamente de tres.

Como nuestro interés radica en un periodo de diez minutos y el número de intervalos de diez minutos en un periodo de 30 minutos es tres, tenemos que el número medio de barras puestas a la venta en ese periodo viene dado por:

\[\lambda = 12/3 = 4.\]

La variable aleatoria que reproduce el número de barras que se venden en una franja de cinco minutos es:

\[N \sim Po(4)\]

En este caso el valor esperado del número de barras que se venden es 4 y la desviación típica es igual a 2($=\sqrt{4}$). En la Figura 1.3 se muestran la fmp y la función de distribución asociadas.

# Valores de N
lambda=4
xs <- seq(0, 10, 1)
# Data frame
datos <- data.frame(xs = xs, probs = dpois(xs, lambda), 
                    probsacum = ppois(xs, lambda))
# función de masa de probabilidad
g1 <- ggplot(datos, aes(xs, probs)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  scale_x_continuous(breaks = 0:10, labels = 0:10) +
  ylim(0,0.3) +
  labs(x ="x", y = "Probabilidad puntual. Pr(N=x)")
# función de distribución
g2 <- ggplot(datos, aes(xs, probsacum)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  scale_x_continuous(breaks = 0:10, labels = 0:10) +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  labs(x ="x", y = "Probabilidad acumulada Pr(N<=x)")
grid.arrange(g1, g2, nrow = 1)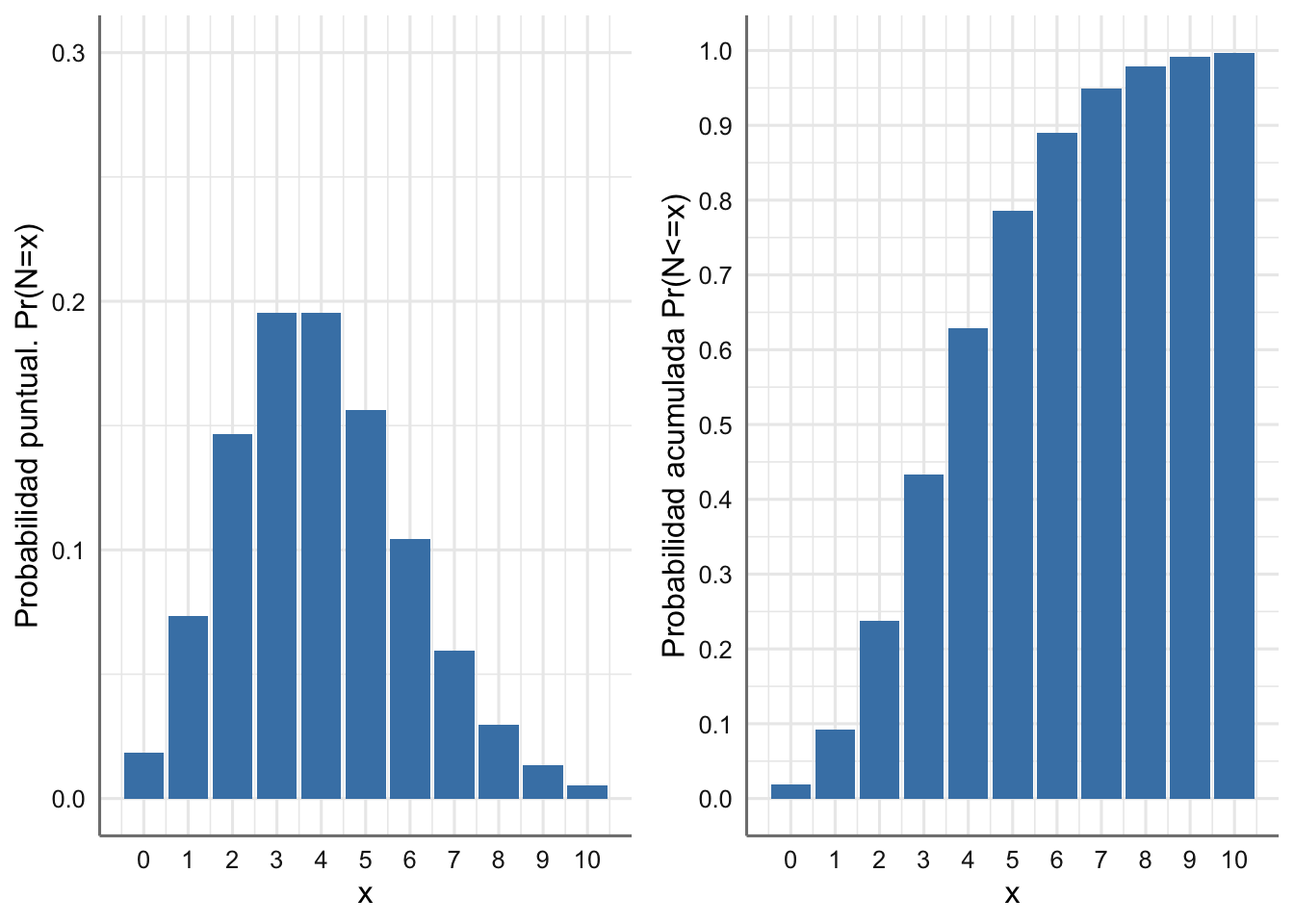

Figura 1.3: Función de masa de probabilidad y Función de distribución para el número de barras de pan que se venden cada cinco minutos.

Podemos reconoder en la Figura 1.3-izquierda los valores más probables con las barras más altas (3 y 4). De hecho, en la Figura 1.3-derecha, la probabilidad de que a lo sumo se vendan menos de 5 barras es algo superior a 0.6.

Para calcular la probabilidad pretendida, esto es, $Pr(N=3)$ utilizamos la función fmp correspondiente en R y la aproximamos por MC con 1000 simulaciones, dando también una banda de confianza.

lambda=4
# Probabilidad buscada P(N=3) para la poisson con media 2
media=dpois(3,lambda)
cat("Pr(N=4)=",round(media,3))

## Pr(N=4)= 0.195

nsim <- 10000
# Simulamos de la poisson y evaluamos la función indicatriz para la prob de interés
set.seed(1970)
I.a <- (rpois(nsim, lambda)==3)*1
# Realizamos la aproximación MC
m=mean(I.a)
cat("AproxMC=",m)

## AproxMC= 0.1934

# Error MC
error=sqrt(sum((I.a-m)^2)/(nsim^2))
# límites del IC redondeados a 3 cifras decimales
ic.low=round(m-qnorm(0.975)*error,3)
ic.up=round(m+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")

## IC(95%)[AproxMC]=[ 0.186 , 0.201 ]

Si la aproximación la hacemos con 10 veces más simulaciones, el intervalo de estimación resultará más preciso:

lambda=4
# Probabilidad buscada P(N=3) para la poisson con media 2
media=dpois(3,lambda)
cat("Pr(N=4)=",round(media,3))

## Pr(N=4)= 0.195

nsim <- 10000*10
# Simulamos de la poisson y evaluamos la función indicatriz para la prob de interés
set.seed(1970)
I.a <- (rpois(nsim, lambda)==3)*1
# Realizamos la aproximación MC
m=mean(I.a)
cat("AproxMC=",m)

## AproxMC= 0.19375

# Error MC
error=sqrt(sum((I.a-m)^2)/(nsim^2))
# límites del IC redondeados a 3 cifras decimales
ic.low=round(m-qnorm(0.975)*error,3)
ic.up=round(m+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")

## IC(95%)[AproxMC]=[ 0.191 , 0.196 ]

Ejemplo 1.9 Una empresa de fabricación de galletas de chocolate está analizando la calidad en su empresa para responder del mejor modo posible a sus clientes. Para ello ha fijado que con probabilidad 0.8 las galletas deben contener al menos tres trozos de chocolate para satisfacer las exigencias de los clientes. Se trata pues de fijar el valor medio de trozos de chocolate que debe ir suministrando en la cadena de producción para cumplir con el nivel de exigencia establecido.

Si $N$ es la variable aleatoria que indica el número de trozos de chocolate en una galleta, tenemos que:

\[N \sim Po(\lambda)\]

donde en este caso el valor de $\lambda$ es desconocido y representa el número medio de trozos de chocolate en cada galleta. Planteamos un estudio de simulación para aproximar dicho valor.

Algoritmo para aproximar el valor de $\lambda$.

Considerar una secuencia de valores de $\lambda_i$, $i=1,...,K$
Obtener una muestra de tamaño $nsim$ para cada distribución $Po(\lambda_i)$, $M_i=\{x_{i_1},\ldots,x_{i_{nsim}}\}$.
Con cada muestra $M_i$ aproximar la probabilidad de que el número de trozos sea mayor o igual a 3, $p_i\approx Pr(N_{\lambda_i}\geq3)$.
Obtener el valor mínimo de $\lambda$, de entre $\{\lambda_1,\ldots,\lambda_K\}$ que verifica $p_i \geq 0.8$.

En la Figura 1.4 se muestra el proceso de simulación realizado a continuación y el resultado obtenido para el valor de $\lambda$ para cumplir los requisitos de la empresa.

# Paso 1
set.seed(1970)
nsim <- 5000
lams <- seq(0.1, 5, 0.01) # valores de lambda
nlams <- length(lams)     # número de lambdas para evaluar
prob <- c()  # vector de probabilidades

# Pasos 2 y 3
for(i in 1:nlams){
  datos <- rpois(nsim, lams[i])    
  prob[i] <- mean(datos >= 3)   
}

# Paso 4. Resultado del problema
lambda=lams[min(which(prob >= 0.8))];lambda

## [1] 4.25

# Pintamos los resultados de la simulación realizada
dat=data.frame(lams=lams,prob=prob)
ggplot(dat,aes(x=lams,y=prob))+
  geom_point()+
  geom_hline(yintercept=0.8)+
  geom_vline(xintercept=lambda)+
  labs(x="lambda",y="Pr(N>=3)")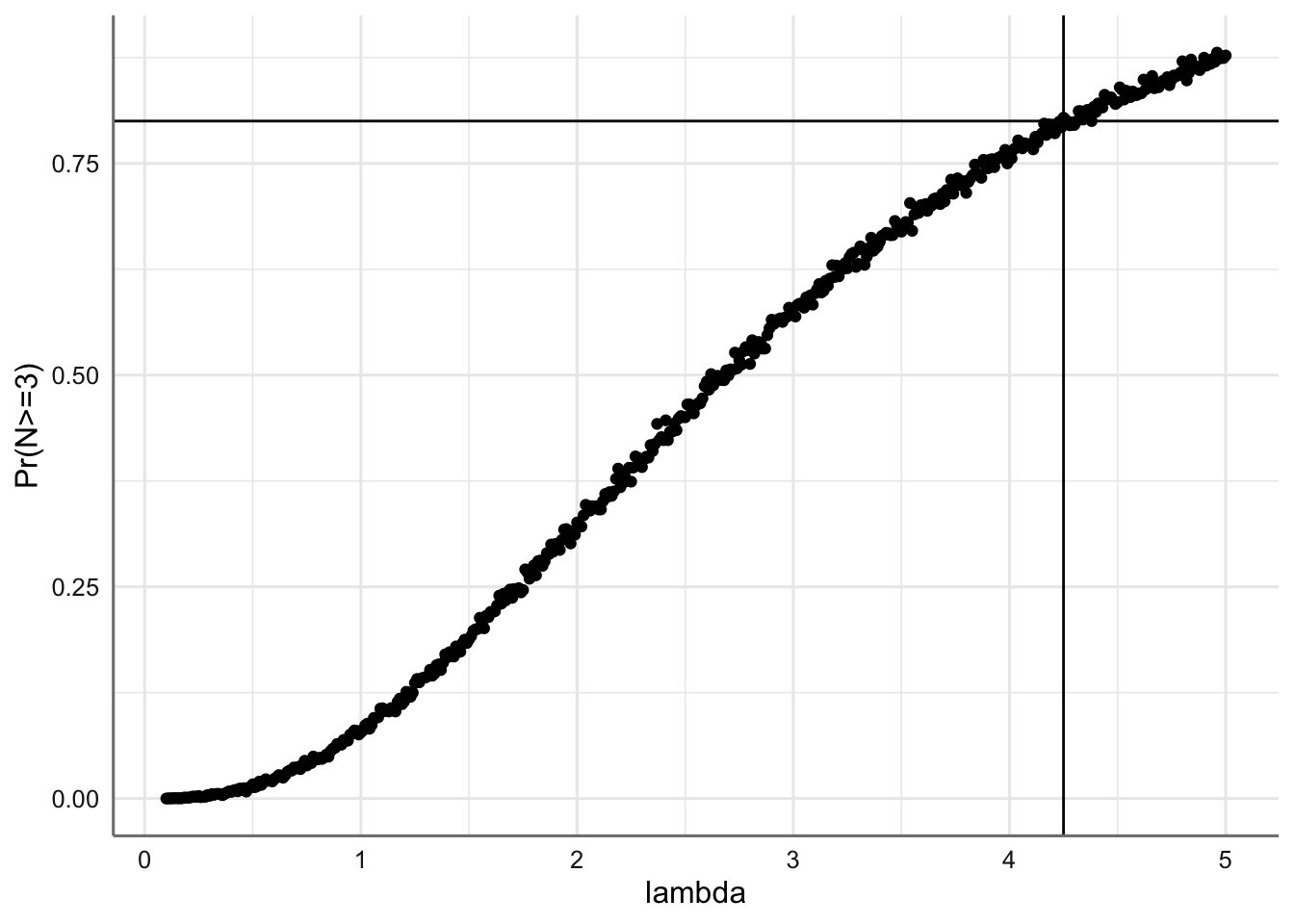

Figura 1.4: Probabilidad estimada de conseguir al menos 3 trozos de chocolate en cada galleta, en función de lambda.

Así pues, el número medio de trozos de chocolate que ha de suministrarse a cada galleta ha de ser al menos de 4.25.

1.4 Distribuciones continuas

En este punto estudiamos las principales variables de tipo continuo. La especificación de estas variables se hace a partir de la función de densidad.

1.4.1 Uniforme

La distribución uniforme es la distribución de probabilidad continua más sencilla y se refiere a eventos infinitos que tienen la misma probabilidad de ocurrir en una intervalo dado. Si $a$ y $b$ son dos números reales con $a < b$ entonces la función de distribución asociada a la probabilidad acumulada a la izquierda de cualquier valor $x \in [a, b]$ viene dada por:

\[\begin{equation} F(x) = \begin{cases} 0 & \text{ si } x < a \\ \frac{x-a}{b-a} & \text{ si } a \leq x \leq b\\ 1 & \text{ si } a \leq x \leq b. \end{cases} \tag{1.12} \end{equation}\]

Definición 1.13 Una variable aleatoria $X$ tiene una distribución uniforme en el intervalo $[a, b]$, con $a,b R,

\[X \sim U(a,b)\]

si su función de densidad viene dada por la expresión

\[\begin{equation} f(x) = \begin{cases} \frac{1}{b-a} & \text{ si } a \leq x \leq b\\ 0 & \text{ en otro caso } \end{cases} \tag{1.13} \end{equation}\]

de forma que $E(X) = (a+b)/2$ y $V(X) = (b-a)^2/12.$

La variable uniforme más famosa es la $U(0,1)$ ya que se utiliza habitualmente para modelizar la incertidumbre sobre una probabilidad desconocida, y es la base para muchos de los algoritmos de simulación de variables y procesos que estudiaremos en el futuro.

La función runif(n, a, b) permite generar $n$ valores de una variable uniforme en el intervalo $[a, b]$; runif(n) da una muestra para una distribución uniforme en [0, 1].
dunif(x,a,b) da la fdp en $x$.
punif(x,a,b) da la probabilidad acumulada para cualquier punto $x \in [a,b]$.

1.4.2 Exponencial

La distribución exponencial es una distribución muy común en la modelización probabilística. Esta distribución describe procesos que describen el tiempo entre sucesos consecutivos, con la peculiaridad de que sus probabilidades no dependen del instante en que se produzcan los eventos. Es decir:

\[Pr(X > t+s | X > t) = Pr(X > s).\]

Esta propiedad es característica de la distribución exponencial y se denomina “propiedad de la pérdida de memoria.”

Ejemplos de este tipo de distribución son:

El tiempo que tarda una partícula radiactiva en desintegrarse. El conocimiento de la ley que sigue este evento se utiliza en ciencias para, por ejemplo, la datación de fósiles o cualquier materia orgánica mediante la técnica del carbono 14.
El tiempo que puede transcurrir en un servicio de urgencias, entre llegadas de pacientes, o en una fábrica entre roturas de una máquina.

Esta distribución está muy relacionada con unos procesos que estudiaremos más adelante, denominados Procesos de Poisson.

La distribución exponencial viene completamente especificada, a través del parámetro $\lambda >0$ que mide el número esperado de veces que ocurre el evento de interés por cada unidad de tiempo, y cuya función de distribución viene dada por:

\[\begin{equation} F(x) = \begin{cases} 0 & \text{ si } x < 0 \\ 1 - e^{\lambda x} & \text{ si } x \geq 0. \end{cases} \tag{1.14} \end{equation}\]

Definición 1.14 Una variable aleatoria $X$ tiene una distribución exponencial de parámetro $\lambda$, que se denota por

\[X \sim Exp(\lambda)\]

si su función de densidad viene dada por

\[\begin{equation} f(x)=\lambda e^{-\lambda x}, \quad x \geq 0, \end{equation}\]

de forma que $E(X) = 1/\lambda$ y $V(X) = 1/\lambda^2.$

Las funciones relacionadas con la distribución exponencial en R son:

La función dexp(x, lambda) nos permite evaluar la función de densidad para una variable poisson de parámetro $\lambda$.
pexp(x, lambda) nos permite evaluar la función de distribución.
rexp(n, lambda) permite generar $n$ valores de una variable Exponencial de parámetro $\lambda$.

A continuación estudiamos dos ejemplos de uso de la distribución exponencial. Como siempre presentamos los resultados téoricos y procedemos mediante simulación para ver la aproximación conseguida.

Ejemplo 1.10 Se ha comprobado que el tiempo de vida de cierto tipo de marcapasos sigue una distribución exponencial con media 16 años. (1) ¿Cuál es la probabilidad de que a una persona a la que se le ha implantado este marcapasos se le deba reimplantar otro antes de 20 años? (2) Si el marcapasos lleva funcionando correctamente 5 años en un paciente, ¿cuál es la probabilidad de que haya que cambiarlo antes de 25 años desde que se implantó?

Si $T$ es la variable aleatoria que indica el tiempo de vida del marcapasos tenemos que:

\[T \sim Exp(\lambda = 1/16)\]

Se puede reponder fácilmente a las preguntas planteadas sin más que hacer uso de la función pexp(). Sin embargo, también simularemos para aproximarlas. Hemos de calcular

(1). Si es preciso implantar antes de 20 años, es porque el tiempo de vida no va a ser superior a 20. Hemos de calcular pues, $Pr(T \leq 20)$. (2). Nos piden $Pr(T \leq 25|T>5)=Pr(T\leq 20)$, por la propiedad de la pérdida de memoria. Es decir, respondiendo a (1) tendremos respondidas las dos preguntas formuladas.

lambda <- 1/16
# Data frame para la representación gráfica
sec <- seq(0, 80, by = 0.01)
datos<- data.frame(sec = sec, densidad = dexp(sec,lambda))
# Gráfico función de densidad
ggplot(datos, aes(sec, densidad)) + 
  geom_line() +
  scale_x_continuous(breaks = seq(0,80,5), labels = seq(0,80,5)) +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  geom_vline(xintercept = 20, col = "red") +
  labs(x ="Tiempo de vida del marcapasos (en años)", 
       y = "Función de densidad")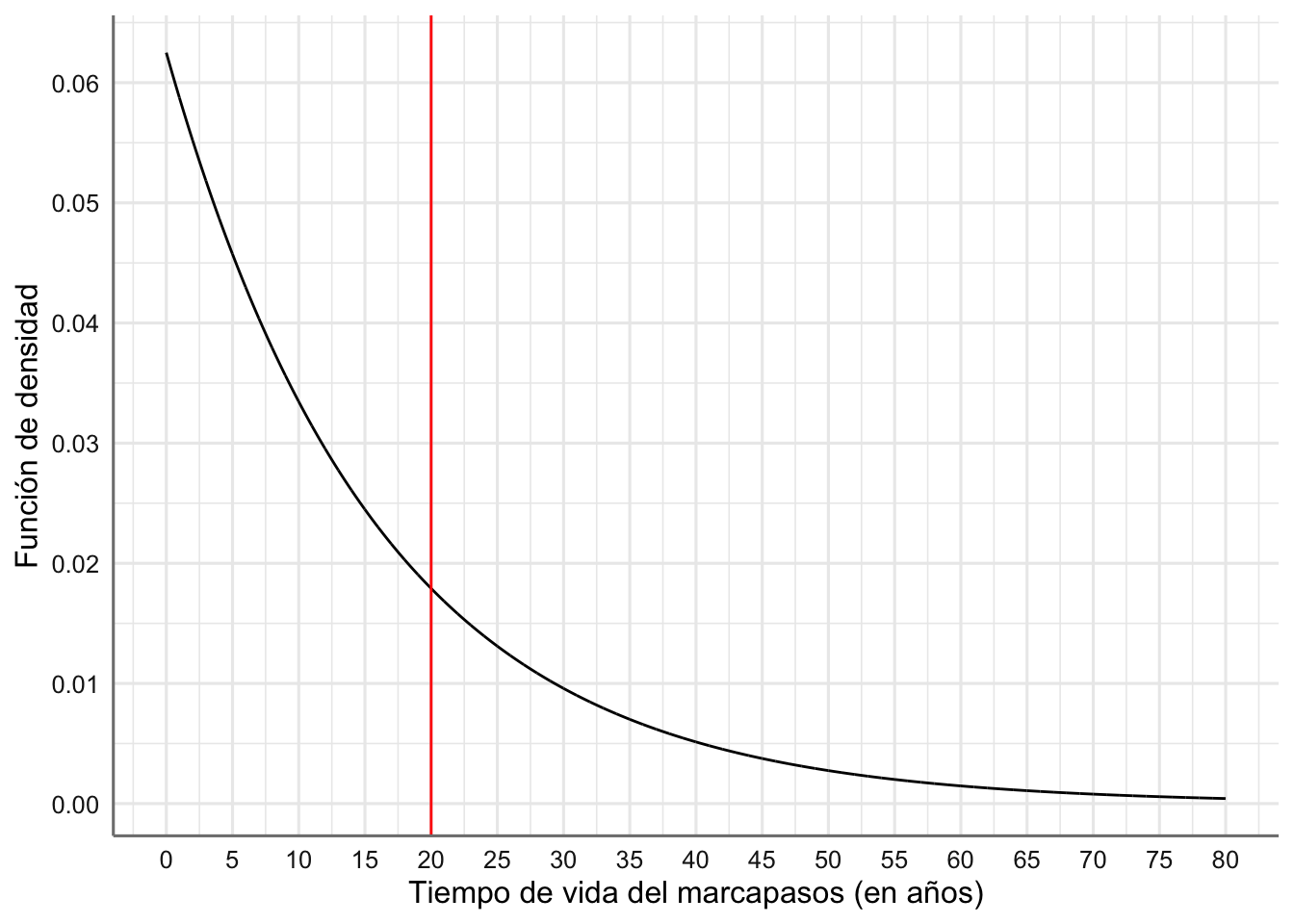

Figura 1.5: Función de densidad del tiempo de vida del marcapasos (en años)

Obtenemos la probabilidad deseada:

# Probabilidad real
lambda=1/16
p=pexp(20,lambda)
cat("Pr(T<=20)=",round(p,3))

## Pr(T<=20)= 0.713

# Parámetros de la simulación
set.seed(123)
nsim <- 5000
# Simulaciones
datos <- rexp(nsim, lambda)
# Probabilidad de interés
pMC=mean(datos <= 20)
cat("Aprox.MC[Pr(T<=20)]=",round(pMC,3))

## Aprox.MC[Pr(T<=20)]= 0.711

La probabilidad de que el marcapasos dure más de 20 años y haya que reemplazarlo es de 0.289, por lo que efectivamente, es muy recomendable reemplazarlo antes. Sin embargo, al paciente en la pregunta (2) se le daría la misma recomendación, cuando la probabilidad de que el marcapasos dure más de 25 años desde su implante, que sería el tiempo que lo llevaría, es considerablemente inferior, 0.21. No es pues recomendable, utilizar esta distribución para modelizar el tiempo de vida de un implante.

Ejemplo 1.11 Un motor eléctrico tiene una vida media de 6 años y se modeliza con una distribución exponencial. ¿Cuál debe ser el tiempo de garantía que debe tener el motor si se desea que a lo sumo el 15 % de los motores fallen antes de que expire su garantía?

Si $T$ es la variable aleatoria que indica el tiempo de vida del producto tenemos que: \[T \sim Exp(\lambda = 1/6).\]
En este caso estamos interesados en encontrar el tiempo para que podamos garantizar que el 85% de los motores siguen funcionando, es decir, buscamos el cuantil 0.15 de la distribución de $T$. Planteamos un análisis de simulación para estimar dicho valor.

# Calculamos el valor real para el periodo de garantía
lambda <- 1/6
q=qexp(0.15,lambda)
cat("Periodo de garantía recomendado=",round(q,2))

## Periodo de garantía recomendado= 0.98

# Parámetros de la simulación
set.seed(123)
nsim <- 5000
# simulaciones
datos <- rexp(nsim, lambda)
# cuantil de interés
qMC=quantile(datos, 0.15)
cat("Periodo de garantía aproximado=",round(qMC,2))

## Periodo de garantía aproximado= 1.02

Para que tan sólo el 15% de los motores necesiten reparación durante el periodo de garantía, debemos establecer una garantía de aproximadamente 1 año.

En la Figura 1.6 se representan, para los datos simulados, los cuantiles aproximados versus su probabilidad asociada. Con el gráfico se puede atisbar también el periodo de garantía recomendado.

# cuantil de interés
probs <- seq(0.05, 0.95, by = 0.05)
cuantiles <- quantile(datos, probs)
datoscuan <- data.frame(probs, cuantiles)
# Gráfico
ggplot(datoscuan, aes(probs,cuantiles)) + 
  geom_line() +
  scale_x_continuous(breaks = probs, labels = probs) +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  geom_vline(xintercept = 0.15, col = "red") +
  labs(x ="Probabilidad", y = "Tiempo a la reparación (en años)")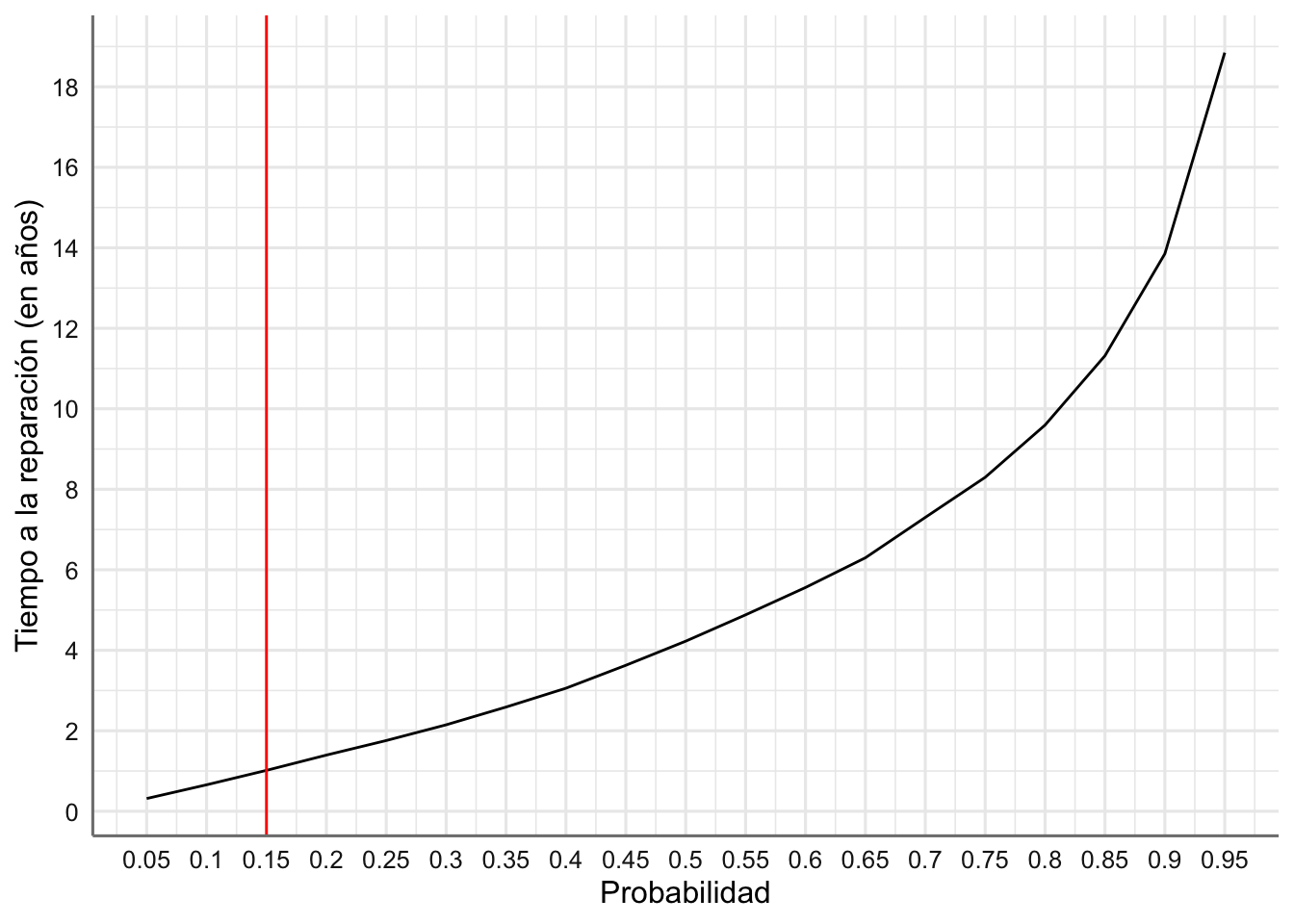

Figura 1.6: Tiempo de garantía recomendado en función de la probabilidad de que los motores necesiten reparación.

Con esta gráfica podemos establecer el tiempo de garantía en función de las especificaciones de la empresa, es decir, fijando el porcentaje de motores que necesitarán reparación.

1.4.3 Gamma

La distribución Gamma, al igual que ocurre con la exponencial, se utiliza habitualmente para modelizar variables aleatorias positivas y asimétricas, y sobre todo para describir procesos de eventos que ocurren en el tiempo. La función de densidad de una variable aleatoria Gamma se caracteriza por dos parámetros: $\alpha$ o parámetro de forma, y $\beta$ o parámetro de escala. El parámetro de forma se denomina así porque al variar su valor se obtienen diferentes formas para la fdp. La variación del parámetro de escala no cambia la forma de la distribución, pero tiende a “estirar” o “comprimir” el rango de valores sobre el que se define la probabilidad.

Definición 1.15 Una variable aleatoria $X$, con $x \geq 0$, tiene una distribución Gamma de parámetros $\alpha > 0$ y $\beta > 0$, denotada por

\[X \sim Ga(\alpha, \beta)\]

si su función de densidad viene dada por la expresión

\[\begin{equation} f(x) = \frac{x^{\alpha -1} e^{-x/\beta}}{\beta^{\alpha} \Gamma(\alpha)}; \quad \text{ para } x \geq 0, \tag{1.15} \end{equation}\]

con $\Gamma()$ la función gamma, de forma que $E(X) = \alpha\beta$ y $V(X) = \alpha\beta^2.$

Un caso especial de la distribución Gamma es la distribución Erlang, que se denota por $X \sim Erlang(k, \beta)$, y que se utiliza habitualmente en la modelización de sistemas de colas de espera. Su función de densidad viene dada por :

\[\begin{equation} f(x) = \frac{k(kx)^{\alpha -1} e^{-xk/\beta}}{\beta^{k} (k-1)!}; \quad \text{ para } x \geq 0, \tag{1.16} \end{equation}\]

con $E(x) = \beta$ y $V(X) = \beta^2/k$. La utilidad de una variable aleatoria Erlang con parámetros $k$ y $\beta$ es que es el resultado de sumar $k$ variables aleatorias exponenciales (independientes) cada una con media $\beta/k$. En la modelización de los tiempos relacionados con un proceso industrial, la distribución exponencial suele ser inadecuada porque la desviación estándar no es tan grande como la media. Los ingenieros suelen tratar de diseñar sistemas que produzcan una desviación estándar de los tiempos del proceso que resulte significativamente menor que su media. La distribución Erlang tiene esta propiedad: su desviación estándar disminuye a medida que aumenta $k$, de modo que los tiempos de proceso con una desviación estándar pequeña a menudo suelen ser aproximados por una variable aleatoria Erlang.

La función dgamma(x, shape, scale) nos permite evaluar la función de densidad para una variable Gamma.
pgamma(x, shape, scale) calcula la función de distribución.
rgamma(n, shape, scale) permite generar $n$ valores de una variable Gamma.

Para simular un dato de una distribución $y \sim (Erlang(k, \beta)$) generamos $k$ datos exponenciales de $x_i \sim Exp(\beta/k), i=1,\ldots,k,$ y calculamos la suma de todos esos valores,$y=\sum_i x_i$. Repetir este proceso tantas veces como indique el tamaño de la muestra simulada que deseamos para la distribución Erlang.

Si disponemos de la media y varianza de los datos resulta muy fácil ajustar los parámetros de la distribución Gamma o Erlang sin más que resolver las ecuaciones que nos dan el valor esperado y la varianza. Si $\bar{x}$ y $s^2$ son respectivamente la media y varianza, podemos ajustar los parámetros de la Gamma con:

\[ \beta = s^2/\bar{x}; \quad \alpha = \bar{x}/\beta\]

mientras que para la Erlang tenemos:

\[ \beta = \bar{x}; \quad k = \bar{x}^2/s^2.\]

A continuación se presenta la función para generar datos Erlang a patir de datos exponenciales:

# Función para generar "nsim" simulaciones de una Erlang 
# con parámetros k (entero) y beta>0
rerlang <- function(nsim, k, beta)
{
  # verificamos que k es entero
  if(k%%1 == 0)
  {
    # parámetro de la exponencial
    lambda <- beta/k
    # Generamos y almacenamos datos exponenciales
    datosexp <- matrix(rexp(nsim*k, lambda), nrow = nsim)
    # Obtenemos la muestra de la Erlang
    datoserl <- apply(datosexp, 1, sum)
    return(datoserl)
  }
  else{
    cat("k debe ser entero")
  }
}

1.4.4 Weibull

La distribución Weibull se utiliza para describir la resistencia a la rotura de diversos materiales o para describir los tiempos de fallo de muchos tipos de sistemas diferentes. La distribución Weibull tiene dos parámetros: un parámetro de escala, $\beta$ , y un parámetro de forma $\alpha$, ambos positivos. La funcion de distribución asociada viene dada por:

\[\begin{equation} F(x) = \begin{cases} 0 & \text{ si } x < 0 \\ 1 - e^{-(x/\beta)^{\alpha}} & \text{ si } x \geq 0 \end{cases} \tag{1.17} \end{equation}\]

Como en el caso de la distribución Gamma el parámetro de forma determina la forma general de la fdp y el parámetro de escala expande o contrae la fdp.

Definición 1.16 Una variable aleatoria $X$ tiene una distribución Weibull de parámetros $\alpha>0$ y $\beta>0$, que se denota por

\[X \sim Weib(\alpha, \beta)\]

si su función de densidad viene dada por la expresión

\[\begin{equation} f(x)=\frac{\alpha}{\beta}\frac{x}{\beta}^{\alpha-1}e^{-(x/\beta)^{\alpha}}, \quad x \geq 0. \tag{1.18} \end{equation}\]

El valor esperado y la varianza vienen dados por:

\[E(X) = \beta \Gamma(1 + 1/\alpha); \quad V(X) = \beta^2 (\Gamma(1 + 2/\alpha) - (\Gamma(1 + 1/\alpha))^2).\]

En R tenemos las siguientes funciones relacionadas con la distribución Weibull.

La función dweibull(x, shape, scale) nos permite evaluar la función de densidad para una variable Weibull
pweibull(x, shape, scale) calcula la función de distribución.
rweibull(n, shape, scale) permite generar $n$ valores de una variable Weibull.

A partir de la media ($\bar{x}$) y varianza ($S^2$) de un conjunto de datos, es posible obtener los parámetros de la distribución Weibull sin más que resolver las ecuaciones:

\[\begin{eqnarray} \beta &=& \frac{\bar{x}}{\Gamma(1 + 1/ \alpha)} \\ \frac{s^2}{\bar{x}^2} - \frac{\Gamma(1+ 2/\alpha)}{(\Gamma(1 + 1/ \alpha))^2} + 1 &=& 0. \tag{1.19} \end{eqnarray}\]

A continuación se propone una función que permite obtener los parámetros a partir de la media y varianza de los datos, junto con un pequeño ejemplo para verificar su funcionalidad.

estima.weibull <- function(m, s)
{
  #m=media, s=desviación típica
  library(rootSolve)
  # Función para optimizar alpha
  fun.alpha <- function(a, m, s)
              {
                res<- 1 + (s/m)^2 - gamma(1+2/a)/(gamma(1+1/a))^2
                return(res)
              }
  # Obtención de alpha
    alpha <- round(uniroot(fun.alpha, c(0.1, 10000),m=m,s=s)$root,2)
  # Obtención de beta
  beta <- round(m/gamma(1+1/alpha), 2)
  # Devolvemos alpha y beta
  return(c(alpha, beta))
}

# Datos de ejemplo
m <- 80     # media
s <- sqrt(50)  # desviación típica
# Estimación
res=estima.weibull(m,s)
cat("Weibull alpha=",res[1],", Weibull beta=",res[2])

## Weibull alpha= 13.83 , Weibull beta= 83.06

1.4.5 Normal

La distribución normal es la distribución más común, reconocida por la mayoría de personas por su curva en forma de “campana,” y también llamada “campana de Gauss.” Aunque la distribución normal no se utiliza mucho en la modelización de procesos y sitemas, es sin duda, la más relevante de las distribuciones aleatorias, ya que representa el supuesto básico distribucional para resolver muchos de los problemas de inferencia estadística habituales, como veremos en la sección final de esta unidad.

Definición 1.17 Una variable aleatoria $X$ tiene una distribución Normal de parámetros $\mu$ y $\sigma$ con $\sigma >0$, denotada por

\[ X \sim N(\mu, \sigma^2),\]

si su función de densidad viene dada por

\[\begin{equation} f(x) = \frac{1}{\sigma\sqrt{2\pi}} exp\left(\frac{-(x-\mu)^2}{2\sigma^2}\right), \quad x \in R \end{equation}\]

con $E(X) = \mu$ y $V(X) = \sigma^2$, y que se denota:

El parámetro $\mu$ identifica la media, y por lo tanto el centro de la distribución al ser simétrica, y el parámetro $\sigma$ la desviación típica.

El caso más destacado es la denominada distribución Normal estándar, para la que $\mu = 0$ y $\sigma = 1$, por su utilización en problemas inferenciales sencillos donde la variabilidad es conocida.

A partir de cualquier distribución Normal podemos transformar a una distribución Normal estándar. Si $X \sim N(\mu, \sigma^2)$ entonces la variable aleatoria $Z$ definida como

\[Z = \frac{X - \mu}{\sigma} \sim N(0,1).\]

Vinculadas a la distribución Normal surgen las distribuciones $t$ de Student, Chi-chadrado y $F$ de Snedecor (también llamada de Fisher-Snedecor), que son ampliamente utilizadas en inferencia estadística. En el último apartado de esta unidad veremos cómo utilizar estas distrbuciones para resolver mediante simulación problemas de intervalos de confianza o contrastes de hipótesis.

Si $\bar{X_n}=\sum_i X_i/n$ representa la media muestral de $n$ v.a. $N(\mu,\sigma)$ y $S^2=\sum_i(X_i-\bar{X_n})^2/(n-1)$ su varianza muestral, entonces la variable $Y$ \[ Y= \frac{\bar{X_n}-\mu}{S/\sqrt{n}}\sim St(n-1)\] sigue una distribución t de Student con $n-1$ grados de libertad, y se denota por $Y\sim St(n-1)$.

Si tenemos un conjunto de variables normales estándar independientes, $X_i\sim N(0,1), i=1,\ldots,n$, entonces su suma al cuadrado sigue una distribución chi-cuadrado con $n$ grados de libertad. \[Z=\sum_{i=1}^n X_i^2 \sim \chi^2_{n}\] Por último, a partir de dos distribuciones chi-cuadrado independientes, $U\sim \chi^2_n$ y $V\sim \chi^2_m$, tenemos que su cociente, corregido por sus grados de libertad, sigue una distribución F de Snedecor con $n$ y $m$ grados de libertad, \[ W=\frac{U/n}{V/m} \sim F_{(n,m)}.\]

Para la distribución Normal,

La función dnorm(x, mean, sd) nos permite evaluar la función de densidad para una variable Normal.
pnorm(x, mean, sd) calcula la función de distribución.
rnorm(n, mean, sd) permite generar $n$ valores de una variable Normal.

Para la distribución t de Student con $df1$ grados de libertad, las funciones correspondientes son dt(x, df1), pt(x, df1) y rt(n,df1).

Para la distribución chi-cuadrado con $df1$ grados de libertad, contamos con las funciones dchisq(x,df1), pchisq(x,df1) y rchisq(n,df1) respectivamente.

Para la distribución F de Snedecor con $df1$ y $df2$ grados de libertad, tenemos las correspondencias df(x, df1, df2), pf(x, df1, df2) y rf(n,df1,df2).

En la Figura 1.7 aparecen representadas varias distribuciones normales con distinta media y varianza.

x=seq(-10,10,0.1)
y1=dnorm(x)
y2=dnorm(x,0,3)
y3=dnorm(x,2,1)
y4=dnorm(x,2,3)
datos=as.tibble(cbind(x,y1,y2,y3,y4))

## Warning: `as.tibble()` was deprecated in tibble 2.0.0.
## Please use `as_tibble()` instead.
## The signature and semantics have changed, see `?as_tibble`.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.

levels=c("N(0,1)"="y1","N(0,3)"="y2","N(2,1)"="y3","N(2,3)"="y4")
datos=datos %>%
  pivot_longer(cols=2:5,names_to="tipo",values_to="valor") 
datos$tipo=fct_recode(datos$tipo,!!!levels)

ggplot(datos,aes(x=x,y=valor,color=tipo))+
  geom_line()+
  labs(color="Distribuciones",y="Función de densidad")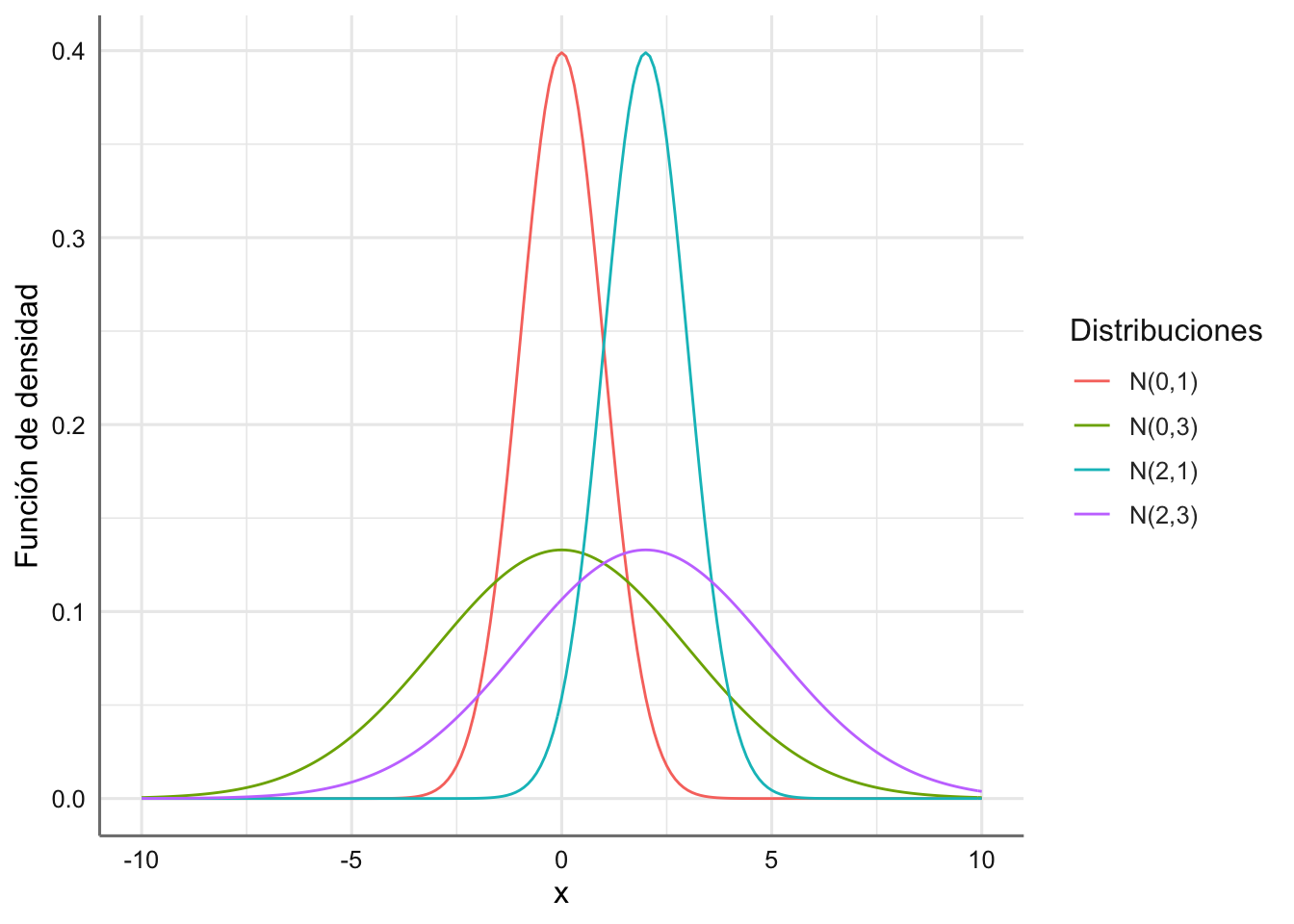

Figura 1.7: Funciones de densidad para varias distribuciones normales.

En la Figura 1.8 aparecen representadas varias distribuciones t de Student con distintos grados de libertad.

x=seq(-5,5,0.1)
y1=dt(x,2)
y2=dt(x,5)
y3=dt(x,10)
y4=dnorm(x)
datos=as.tibble(cbind(x,y1,y2,y3,y4))
levels=c("St(2)"="y1","St(5)"="y2","St(10)"="y3","N(0,1)"="y4")
datos=datos %>%
  pivot_longer(cols=2:5,names_to="tipo",values_to="valor") 
datos$tipo=fct_recode(datos$tipo,!!!levels)

ggplot(datos,aes(x=x,y=valor,color=tipo))+
  geom_line()+
  labs(color="Distribuciones",y="Función de densidad")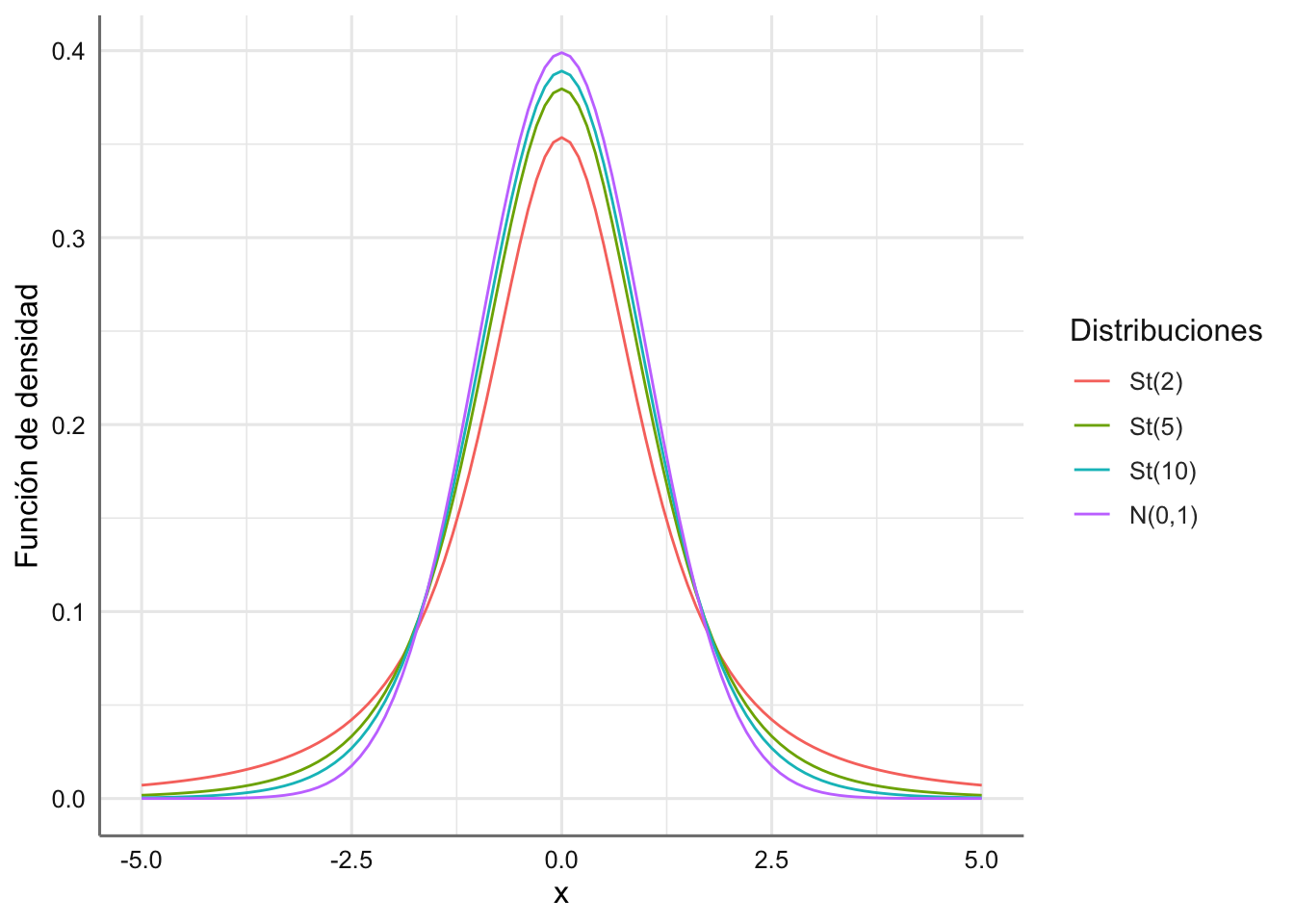

Figura 1.8: Funciones de densidad para varias distribuciones T de Student.

En la Figura 1.9 aparecen representadas varias distribuciones chi-cuadrado con distintos grados de libertad.

x=seq(0,200,0.1)
y1=dchisq(x,5)
y2=dchisq(x,10)
y3=dchisq(x,50)
y4=dchisq(x,100)
datos=as.tibble(cbind(x,y1,y2,y3,y4))
levels=c("Chi2(5)"="y1","Chi2(10)"="y2","Chi2(50)"="y3","Chi2(100)"="y4")
datos=datos %>%
  pivot_longer(cols=2:5,names_to="tipo",values_to="valor") 
datos$tipo=fct_recode(datos$tipo,!!!levels)

ggplot(datos,aes(x=x,y=valor,color=tipo))+
  geom_line()+
  labs(color="Distribuciones",y="Función de densidad")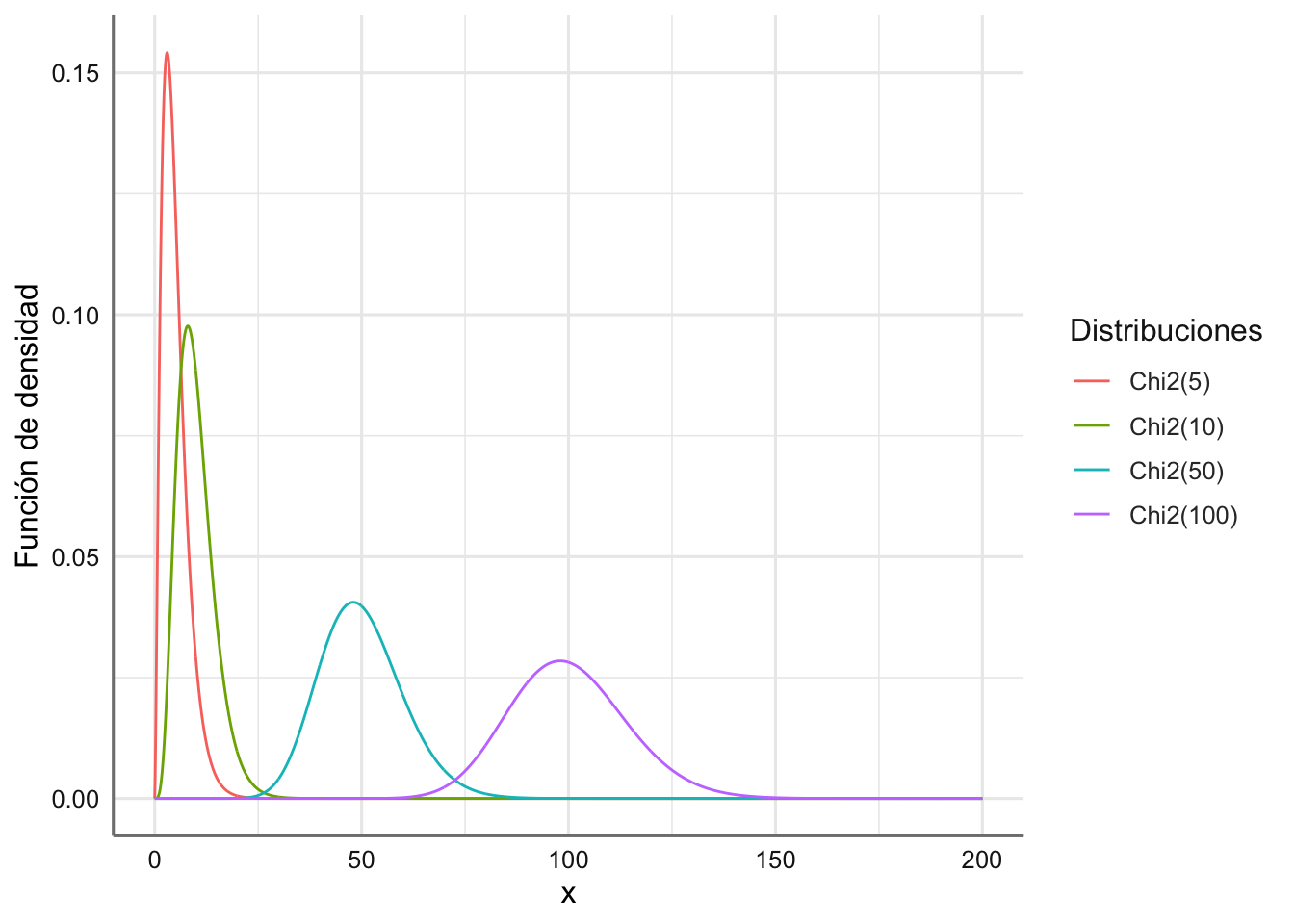

Figura 1.9: Funciones de densidad para varias distribuciones Chi-cuadrado.

En la Figura 1.10 aparecen representadas varias distribuciones F de Snedecor con distintos grados de libertad.

x=seq(0,5,0.01)
y1=df(x,5,5)
y2=df(x,1,5)
y3=df(x,50,10)
y4=df(x,100,200)
datos=as.tibble(cbind(x,y1,y2,y3,y4))
levels=c("F(5,5)"="y1","F(1,5)"="y2","F(50,10)"="y3","F(100,200)"="y4")
datos=datos %>%
  pivot_longer(cols=2:5,names_to="tipo",values_to="valor") 
datos$tipo=fct_recode(datos$tipo,!!!levels)

ggplot(datos,aes(x=x,y=valor,color=tipo))+
  geom_line()+
  labs(color="Distribuciones",y="Función de densidad")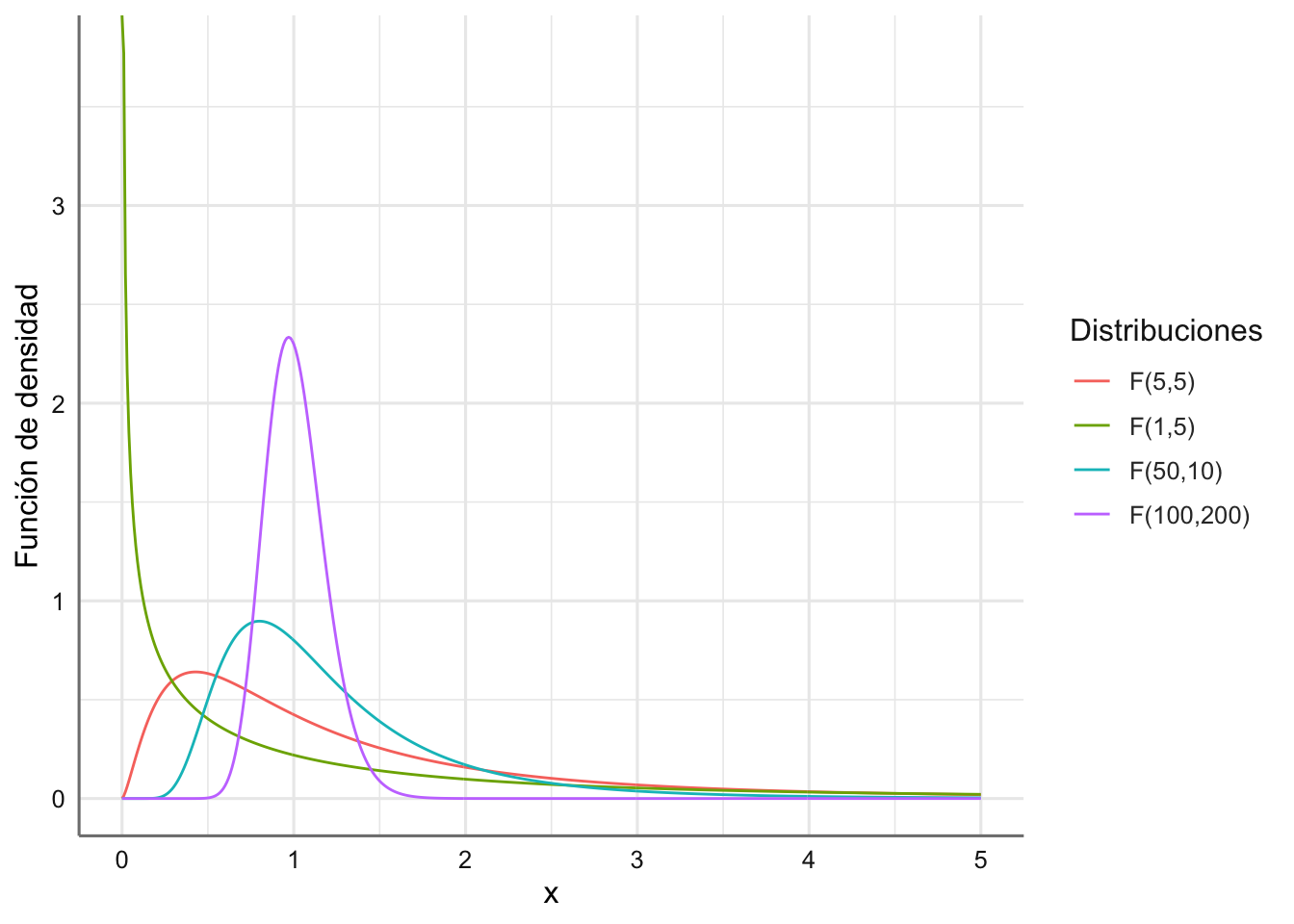

Figura 1.10: Funciones de densidad para varias distribuciones F-Snedecor.

1.5 Simular con la Transformada Inversa

Aunque las distribuciones estudiadas en el punto anterior, al ser habituales provocan que los algoritmos de simulación y sus funciones de probabilidad ya estén implementadas en la mayoría de los paquetes estadísticos y de cálculo, en otras ocasiones, ante otras distribuciones menos comunes, no disponemos de un método directo para la simulación de muestras aleatorias, y necesitamos recurrir a algoritmos genéricos de simulación de variables.

Presentamos a continuación un algoritmo genérico para simular de variables discretas o continuas definidas a trozos: el algoritmo de la transformada inversa, que pasamos a describir, tanto para variables continuas como para variables discretas.

Definición 1.18 Algoritmo de la transformada inversa para variables continuas

Dada una variable aleatoria $X$ de tipo continuo, cuya función de distribución viene dada por $F(x)$, y cuya función de distribución inversa se denota por $F^{-1}(x)$, el algoritmo de la transformada inversa permite obtener una muestra de tamaño $n$ de la variable $X$ mediante el siguiente procedimiento:

Generar $n$ valores uniformes en el intervalo $[0,1]$,

\[u_i\sim U(0,1), \quad i=1,...,n\]

Devolver $x_i = F^{-1}(u_i)$.

Así los valores $\{x_1,...,x_n\}$ constituyen una muestra de $X$.

El algoritmo es conceptualmente similar para variables discretas, si bien por la discretización, varía levemente.

Definición 1.19 Algoritmo de la transformada inversa para variables discretas

Dada una variable aleatoria $X$, de tipo discreto, con $k$ posibles valores diferentes $x_1,...,x_k$, y cuya función de distribución viene dada por:

\[F(x) = Pr(X \leq x) = \sum_{x_i \leq x} Pr(X = x_i), i=1,...,k,\]

el algoritmo de la transformada inversa permite obtener una muestra de tamaño $n$ de la variable $X$ mediante el siguiente procedimiento:

Generar $n$ valores uniformes en el intervalo $[0,1]$, \[u_i\sim U(0,1), \quad i=1,...,n\]
Para cada $u_i$ generado se determina el entero $I$ más pequeño que satisface $u_i \leq F(x_I)$, del conjunto $\{x_1,...,x_k\}$
Devolver $x_I$ para cada valor simulado.

Así los valores $\{x_1,...,x_n\}$ constituyen una muestra de $X$.

En los puntos siguientes vamos a mostrar el uso de los algoritmos 1.18 y 1.19 en diferentes ejemplos de variables de tipo discreto y continuo.

1.6 Otras distribuciones discretas

Analizamos diferentes ejemplos en los que estamos interesados en evaluar un sistema que involucra a una o más variables de tipo discreto, y donde únicamente disponemos de información sobre la función de masa de probabilidad o sobre la función de distribución.

1.6.1 Una variable discreta

Supongamos un sistema en el que contamos con información de una única variable discreta de interés que deseamos estudiar. En los casos más sencillos que tratamos aquí, las situaciones planteadas se pueden resolver teóricamente sin mucha dificultad, pero el objetivo es mostrar el uso de la simulación para llegar a resultados aproximados a los que proporcionan los métodos análiticos.

Ejemplo 1.12 Una empresa que fabrica piezas para maquinaria de fabricación de calzado tiene diseñada la cadena de producción de tal forma que las piezas fabricadas se almacenan (y venden) en cajas de dos unidades. El beneficio estimado de una caja sin defectos es de 300 euros. La política de la empresa establece que si al servir una caja a los clientes, esta contiene una pieza defectuosa, debe ser devuelta de forma inmediata para su reemplazo, lo que supone una pérdida de 50 euros por pieza defectuosa (y la devolución de los 300 euros de beneficio por la venta). El problema es que una vez cerradas las cajas en la cadena de producción no se inspeccionan para estimar el número de cajas que se podrían devolver. La única información disponible hace referencia a la tasa de defectos observada en cada caja cuando esta es devuelta, junto con el porcentaje de cajas que son devueltas. En base a esta información, si $N$ refleja el número de piezas defectuosas observadas, la empresa ha establecido que:

\[\begin{equation} Pr(N = k) = \begin{cases} 0.82 & \text{ para } k = 0\\ 0.15 & \text{ para } k = 1\\ 0.03 & \text{ para } k = 2\\ \end{cases} \tag{1.20} \end{equation}\]

La empresa quiere estudiar el beneficio estimado de acuerdo a la politica de producción actual para el próximo mes, sabiendo que se pueden llegar a producir hasta 1500 cajas en ese periodo. Además la empresa está interesada en conocer el beneficio estimado si cambiara su politica de calidad reduciendo su tasa de defectos por caja de acuerdo a las siguientes proporciones:

\[\begin{equation} Pr(N = k) = \begin{cases} 0.85 & \text{ para } k = 0\\ 0.13 & \text{ para } k = 1\\ 0.02 & \text{ para } k = 2\\ \end{cases} \tag{1.21} \end{equation}\]

Para resolver las inquietudes de la empresa, vamos a simular el proceso en las dos situaciones planteadas, para el horizonte propuesto de un mes, esto es, simulando las 1500 cajas y estimando el beneficio obtenido de acuerdo a las políticas de calidad dadas en (1.20) y (1.21).

Proponemos el siguiente algoritmo de simulación para obtener la ganancia asociada a cada una de las políticas de calidad, y con dichas ganancias compararlas y concluir cuál es la más beneficiosa.

Algoritmo de simulación Ante una política de calidad:

Fijar las condiciones de simulación: nº cajas ($nsim = 1500$).
Obtener las función de distribución acumulada vinculada con la politica de calidad de interés y aplicar el algoritmo dado en al definición 1.19 para obtener una muestra de $N$, $x_1,...,x_n$, relativas al número de piezas defectuosas en cada caja.
Calcular el beneficio obtenido para cada caja, vinculado a cada valor $x_i$, denominado $b_i$.
Obtener la ganancia global con todas las cajas simuladas como:

\[G = \sum_{i=1}^n b_i\]

Lancemos el algoritmo para cada situación y obtengamos los beneficios esperados.

# Parámetros de la simulación
set.seed(19)
nsim <- 1500
# datos uniformes
unif <- runif(nsim)
# Valores a devolver (piezas defectuosas por caja)
valores <- c(0, 1, 2)
# Valores a devolver y probabilidad acumulada para la política 1
prob1 <- c(0.82, 0.15, 0.03)
probacum1 <- cumsum(prob1)
# Valores a devolver y probabilidad acumulada para la política 2
prob2 <- c(0.85, 0.13, 0.02)
probacum2 <- cumsum(prob2)
# Inicialización de variables donde almacenamos las simulaciones
xs1 <- c(); benef1 <- c()
xs2 <- c(); benef2 <- c()
# Simulación de la variable de interés
i <- 1
while (i <= nsim)
{
  # politica 1
  xs1[i] <- valores[min(which(unif[i] <= probacum1))] 
  benef1[i] <- ifelse(xs1[i]==0, 300, -50*xs1[i]) # beneficios
  # politica 2
  xs2[i] <- valores[min(which(unif[i] <= probacum2))]  
  benef2[i] <- ifelse(xs2[i]==0, 300, -50*xs2[i])
    # nueva simulación
  i <- i+1
}
# Resultados para las nsim simulaciones
simulacion <- data.frame(defec.s1 = xs1, benef.s1 = benef1, 
                         defec.s2 = xs2, benef.s2 = benef2)
cat("Una muestra de las simulaciones realizadas es ...\n")

## Una muestra de las simulaciones realizadas es ...

head(simulacion)

##   defec.s1 benef.s1 defec.s2 benef.s2
## 1        0      300        0      300
## 2        0      300        0      300
## 3        0      300        0      300
## 4        0      300        0      300
## 5        0      300        0      300
## 6        0      300        0      300

# Rendimientos globales
beneficios=simulacion %>% 
  summarise(G1 = sum(benef.s1), G2 = sum(benef.s2), 
                         Dif = G2 - G1)
cat("Beneficios S1 (€):",beneficios$G1,
    "Beneficios S2 (€):",beneficios$G2,
    "Diferencia S2-S1 (€):",beneficios$Dif)

## Beneficios S1 (€): 350950 Beneficios S2 (€): 367200 Diferencia S2-S1 (€): 16250

En consecuencia, se aprecia cómo una leve mejora de la calidad en la producción (reduciendo la tasa de defectos) proporciona a la empresa una ganancia sustancial, por lo que la política S2 sin duda es la más ventajosa para su negocio.

Ejemplo 1.13 Una empresa de inversiones está considerando tres nuevos planes de inversión. Cada plan requiere una inversión de 25.000 dólares y el retorno será un año después. El plan A retornará de forma fija 27.500 dólares. El plan B retornará 27.000 dólares o 28.000 dólares, con probabilidades 0.4 y 0.6, respectivamente. El plan C retornará 24.000, 27.000 o 33.000 dólares con probabilidades de 0.2, 0.5 y 0.3, respectivamente. Si el objetivo de la empresa es maximizar el rendimiento esperado, ¿qué plan debería elegir?

Hay que tener en cuenta que en este caso no sólo es relevante el rendimiento esperado, sino también la volatilidad esperada para ese beneficio, expresada en términos de variabilidad o incertidumbre. Será pues interesante, calcular el rendimiento o el retorno esperado en cada situación, además de su varianza o desviación típica.

Vamos a plantear un proceso de simulación para estimar los beneficios y volatilidad asociadas a cada plan. Fijaremos el mismo número de simulaciones en cada plan, con el fin de hacer comparables los resultados. El algoritmo se presenta a continuación.

Algoritmo de simulación

Fijar condiciones de simulación ($nsim = 1000$)
Obtener la función de distribución acumulada vinculada con cada uno de los planes de inversión y aplicar el algoritmo dado en la definición 1.19 para obtener una muestra de cada uno de ellos.
Calcular el beneficio obtenido para cada simulación en cada plan.
Obtener la ganancia estimada de cada plan como la media de los beneficios obtenidos para cada simulación, y la volatilidad como la desviación típica de los beneficios obtenidos.

Y procedemos con la simulación, calculando el beneficio esperado y la desviación típica en cada plan de inversión. Considerando que el plan A no tiene incertidumbre alguna (Varianza=0) y el beneficio fijo que generará será de $2500, no lo incluimos en la simulación.

# Parámetros de la simulación
set.seed(1970)
nsim <- 1000
# datos uniformes
unif <- runif(nsim)
# Beneficios asociados a cada plan
BpB <- c(2000, 3000)  # beneficio variable
BpC <- c(-1000, 2000, 8000) # beneficio variable
# Distribuciones de probabilidiad para los planes B y C
probB <- c(0.4, 0.6)
probacumB <- cumsum(probB) # función de distribución plan B
probC <- c(0.2, 0.5, 0.3)
probacumC <- cumsum(probC) # función de distribución plan 
# Inicialización de variables donde almacenamos las beneficios 
# individuales para cada simulación
benefB <- c()
benefC <- c()
# Simulación de la variable de interés
i <- 1
while (i <= nsim)
{
  # plan B
  benefB[i] <- BpB[min(which(unif[i] <= probacumB))] 
  # plan C
  benefC[i] <- BpC[min(which(unif[i] <= probacumC))]  
  # nueva simulación
  i <- i+1
}
# Resultado
simulacion <- data.frame(A=rep(2500,nsim),B = benefB, C = benefC)
cat("Una muestra de las simulaciones realizadas es ...\n")

## Una muestra de las simulaciones realizadas es ...

head(simulacion)

##      A    B     C
## 1 2500 2000 -1000
## 2 2500 3000  8000
## 3 2500 2000 -1000
## 4 2500 2000 -1000
## 5 2500 3000  8000
## 6 2500 3000  8000

beneficios=simulacion %>% 
  summarise(mPB = mean(B), sdPB = sd(B), 
            mPC = mean(C), sdPC = sd(C))

cat("Beneficios PlanA ($):",2500,
    "Volatilidad (sd):",0,
   "Beneficios PlanB ($):",beneficios$mPB,
    "Volatilidad (sd):",beneficios$sdPB,
    "Beneficios PlanC ($):",beneficios$mPC, 
    "Volatilidad (sd):",beneficios$sdPC)

## Beneficios PlanA ($): 2500 Volatilidad (sd): 0 Beneficios PlanB ($): 2604 Volatilidad (sd): 489.3091 Beneficios PlanC ($): 3122 Volatilidad (sd): 3315.435

Podemos ver que aunque el plan C es el que proporcioanrá más retorno esperado, también es el que tiene una mayor volatilidad (sd), lo que produce incertidumbre y podría repercutir en una mayor pérdida al final del periodo de inversión. El plan A tiene un beneficio fijo sin volatilidad ninguna, pero es inferior al beneficio del plan B. A efetos estadísticos, ya que la volatilidad (desviación típica) del plan B toma un valor inferior a la media, el coeficiente de variación ($cv=sd/media$) resulta inferior a 1, y en consecuencia da una alternativa razonable al plan A. Por contra, no ocurre así en el plan C ($cv>1$) lo que lo coloca en una situación de inferioridad frente a los otros planes de inversión.

Con el fin de afinar en nuestra comparación de los tres planes de inversión, no nos vamos a conformar con valores esperados y desviaciones típicas, y vamos a calcular la probabilidad de que beneficio obtenido sea mayor a 2500 dólares con cada plan, cálculo que podemos resolver fácilmente a partir de las simulaciones obtenidas.

# Probabilidad beneficio > 2500
c(prA = sum(simulacion$A>2500)/1000, 
  prB = sum(simulacion$B>2500)/1000, 
  prC = sum(simulacion$C>2500)/1000)

##   prA   prB   prC 
## 0.000 0.604 0.289

Con este cálculo, el plan B sale claramente reforzado, con una probabilidad destacable de generar un beneficio superior a $2500 (prob=0.6), frente al plan A (prob=0) y al C (prob=0.29). El plan A no puede superar unos rendimientos superiores a 2500, al ser este valor su fijo.

1.6.2 Mixturas de Discretas

Estas situaciones son muy habituales e involucran la combinación de diferentes variables de tipo discreto en un mismo sistema, en lo que se viene a denominar mixtura de variables aleatorias de tipo discreto o modelos secuenciales. Sobre este tipo de distribuciones resulta bastante sencillo plantear un algoritmo de simulación. Antes de comenzar veamos desde un punto de vista téorico el concepto de mixtura de variables.

Definición 1.20 Sean $X_1, X_2,...,X_n$ un conjunto de variables aleatorias independientes de tipo discreto y sea $I$ una variable indicador de tipo discreto, definida en los valores $\{1,..., n\}$, tal que \[Pr(I=j)=p_j, j=1,..., n, \quad \sum_{j=1}^n p_j = 1.\]

La variable aleatoria $T$ que se define como:

\[ T = \sum_{j =1}^n p_j X_j\]

se denomina mixtura del conjunto $X_1,...,X_n$ con índice $I$, y además cumple que:

\[E(T) = \sum_{j=1}^n p_j E(X_j)\]

\[E(T^2) = \sum_{j=1}^n p_j (V(X_j) + E(X_j)^2).\]

Así, la varianza de $T$ se puede calcular fácilmente a partir de la expresión:

\[V(T) = E(T^2) - E(T)^2\]

El algoritmo para simular de una mixtura es bastante sencillo y se basa en la aplicación consecutiva en dos pasos del algoritmo de la transformada inversa para variables discretas en la Definición 1.19.

Definición 1.20 Algoritmo simulación mixtura variables discretas

En la situación descrita en la definición 1.20 el algoritmo para generar una muestra de la mixtura debe proporcioanr en cada simulación un vector de dos componentes: variable seleccionada ($I$) y valor generado de $X_I$. En concreto:

Paso 1. Establecer el tamaño de muestra a simular $nsim$.

Repetir los pasos 2 y 3 para cada iteración $i$ de $1, 2,..., nsim$:

Paso 2. Simular un valor para el indicador $I_i$ de la variable de mixtura, mediante el algoritmo de la transformada inversa para una variable discreta (Definición 1.19) con probabilidades $p_1,...,p_n$, y seleccionar la variable $X_{I_i}$ para dicho indicador.
Paso 3. Simular un valor $x_{I_i}$ mediante el algoritmo de la transformada inversa para $X_i$.
Paso 4. Devolver el conjunto de simulaciones $\{I_i, x_{I_i}\}_{i=1}^{nsim}.$

Pasamos a estudiar un par de ejemplos de situaciones secuenciales para variables discretas que se pueden modelizar según una mixtura y donde podemos aplicar el algoritmo anterior.

Ejemplo 1.14 Una tienda de electrodomésticos desea analizar las ventas de hornos microondas. Los gerentes de la tienda saben que en muchas ocasiones la gente entra en la tienda simplemente para curiosear, pero de todas las personas con intenciones claras de compra, el 50% acaba comprando uno de los tres modelos disponibles y el otro 50% finalmente no realiza ninguna compra. De los clientes que compran un horno, el 25% adquiere el modelo sencillo, el 50% el modelo estándar y el 25% el modelo de lujo. El modelo sencillo produce una ganancia de 30 dólares; el modelo estándar produce una ganancia de 60 dólares y el modelo de lujo produce una ganancia de 75 dólares.

Los gerentes están interesados en estimar el beneficio medio por cliente de todos aquellos con intención de comprar, y que por tanto utilizan el asesoramiento (y tiempo) de los vendedores.

El enfoque habitual para estimar el beneficio promedio sería mantener registros de todos los clientes que hablan con los vendedores y calcular con esos datos una estimación del beneficio esperado por cliente. Sin embargo, este proceso puede ser simulado sin mucha dificultad a partir de la información proporcionada, para estimar, por ejemplo, el beneficio promedio por cliente para los próximos cien clientes.

Este proceso se puede describir mediante una mixtura con dos variables $X_0$ y $X_1$ que expresan cuál es el beneficio que genera un cliente que entra en la tienda, mediante una variable indicador $I$, que identifica si un cliente está interesado o no en comprar.

Sea $X_i$ la ganancia generada por cada cliente que entra a la tienda, para cada uno de los tipos de cliente: 0=no compra, 1=sí compra: \[X_i, \quad i=0,1\]

La probabilidad de que un cliente compre o no viene dada por: \[\begin{equation*} Pr(I = i)= \begin{cases} 0.5 & i=1 \text{ (si compra)} \\ 0.5 & i=0 \text{ (si no compra) } \end{cases} \end{equation*}\]

De modo que un cliente que no compra produce beneficios 0 con probabilidad 1,

\[Pr(X_0=0)=1,\] y el beneficio de un cliente que no compra tiene como distribución de probabilidad:

\[\begin{equation*} Pr(X_1 = k) = \begin{cases} 0.25 & \text{ para } k = 30 \text{ modelo sencillo}\\ 0.50 & \text{ para } k = 60 \text{ modelo estándar}\\ 0.25 & \text{ para } k = 75 \text{ modelo lujo}. \end{cases} \end{equation*}\]

Es fácil simular cualquiera de estas distribuciones discretas mediante el algoritmo de la transformada inversa para variables discretas en la Definición 1.19, para acabar simulando de $T$ con el algoritmo anterior en la Definición 1.20.

Simulemos pues el proceso de venta para 30 clientes, recopilando, además de la ganancia que genera cada uno, la ganancia acumulada por las compras realizadas. Construimos una función para simular el proceso, en la que introducimos como parámetros la semilla de inicialización de la simulación y el número de clientes, por si deseamos ampliar el espectro de simulación en algún momento.

simula.ventas.micro <- function(clientes, semilla)
{
# Descripción del proceso de compra o no compra
compra <- c("Si", "No")
pcompra <- 0.50
# Descripción del proceso de adquisión del microondas
tipo <- c("Sencillo", "Estándar", "Lujo")
prmicro <- c(0.25, 0.50, 0.25) # fmp X1
prmicroacum <- cumsum(prmicro) # fon. distribución X1
beneficio <- c(30, 60, 75)
# Inicialización de variables para las simulaciones
indicador <- c()             # proceso de compra
micro <- c()                 # tipo microondas adquirido
bind <- rep(0, clientes)     # beneficio individual
bacum <- rep(0, clientes)    # beneficio acumulado

## Simulación del proceso
##########################
i <- 1
# Generamos uniformes para describir el proceso de compra y 
# el tipo de microondas adquirido
set.seed(semilla)
ucompra <- runif(clientes) # uniformes para el indicador
umicro <- runif(clientes)  # uniformes para la compra

# Bucle de simulación
while (i <= clientes)
{
  # Proceso de compra
  indicador[i] <- ifelse(ucompra[i] <= 0.5, compra[1], compra[2])
  # Tipo de microndas
  if(indicador[i] == compra[1])
  {
    pos <- min(which(umicro[i] <= prmicroacum))
    micro[i] <- tipo[pos]
    bind[i] <- beneficio[pos]
  }
  else
  {
    micro[i] <- "Sin venta"
    bind[i] <- 0
  }
  bacum[i] <- sum(bind[1:i])  # se acumulan todos los beneficios
  # nueva simulación
  i <- i+1
}
# Resultado
return(data.frame(Compra = indicador, Tipo = micro, 
                  Bind = bind, Bacum = bacum))
}

Generamos el proceso para 30 clientes y analizamos los resultados

simulacion <- simula.ventas.micro(30, 123)
head(simulacion)

##   Compra      Tipo Bind Bacum
## 1     Si      Lujo   75    75
## 2     No Sin venta    0    75
## 3     Si  Estándar   60   135
## 4     No Sin venta    0   135
## 5     No Sin venta    0   135
## 6     Si  Estándar   60   195

# el beneficio acumulado tras el paso de 30 clientes
tail(simulacion,n=1)

##    Compra     Tipo Bind Bacum
## 30     Si Estándar   60   600

El beneficio acumulado tras el paso de 30 clientes un día cualquiera que hemos simulado es de 600 dólares.

En la Figura 1.11 se han representado los resultados de las simulaciones generadas (30 clientes que pasan a la tienda), así como los beneficios acumulados por las ventas realizadas.

g1=simulacion %>%
  group_by(Tipo) %>%
  summarise(n=n()) %>%
  mutate(prop=n/nrow(simulacion)) %>%
  ggplot(aes(x = Tipo, y = prop)) +
    geom_col(aes(fill = Tipo), position = "dodge") +
    geom_text(aes(label = scales::percent(prop), 
                  y = prop, group = Tipo),
              position = position_dodge(width = 0.9),
              vjust = 1.5)+
  labs(x="Tipo de cliente",y="Proporción")+
  theme(legend.position="none")

g2 <- ggplot(simulacion, aes(1:30, Bacum)) + 
  geom_line() +
  labs(x = "Cliente", y = "Beneficio acumulado")
grid.arrange(g1, g2, nrow = 1)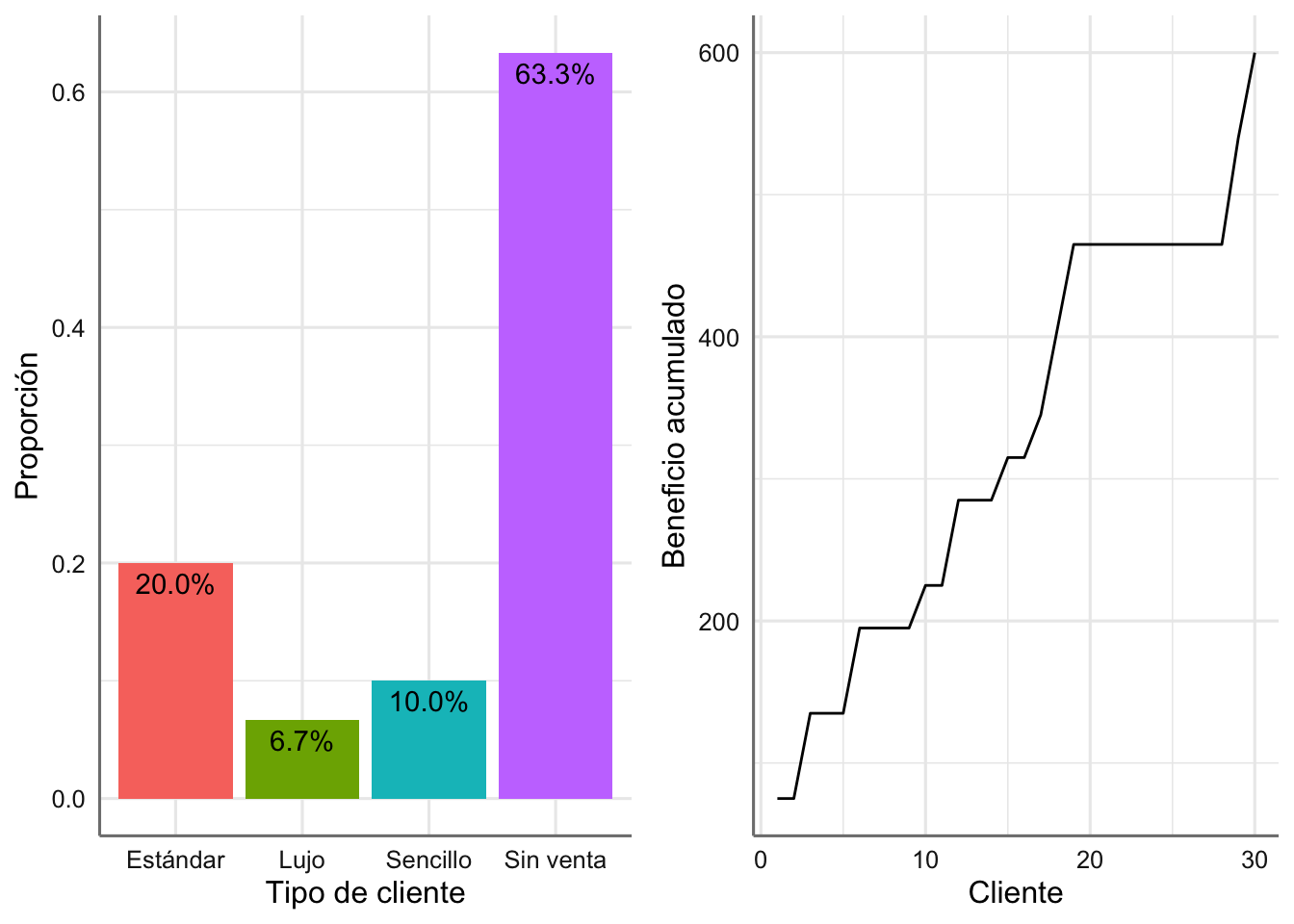

Figura 1.11: Frecuencia relativa de cada tipo de venta (izquierda) y beneficio acumulado para los 30 clientes (derecha).

Podemos también calcular la ganancia promedio que se obtiene con esos 30 clientes a partir de la variable simulaciones$Bind, que resulta de

mean(simulacion$Bind)

## [1] 20

Si queremos aproximar el beneficio esperado por cliente, bastará simular muchos clientes, y promediar los beneficios que le dan a la tienda, o incluso el beneficio esperado por cliente que compra un microondas.

nsim <- 1000 # número de clientes simulados
simulacion <- simula.ventas.micro(nsim,123)
# aproximación MC del beneficio medio de un cliente cualquiera
mean(simulacion$Bind)

## [1] 29.025

# beneficio medio de un cliente de compra
mean(simulacion$Bind[simulacion$Compra=="Si"])

## [1] 57.24852

Así, el beneficio medio por cliente es aproximadamente de 29.03 dólares, mientras que el beneficio esperado por cliente que compra un microondas es de 57.25 dólares. El beneficio esperado por cada 30 clientes que entran en la tienda será de $20.025 \times 30=870.75$ dólares.

Ejemplo 1.15 Un fabricante de galletas presenta muchos productos nuevos cada año, de los cuales cerca del 60% fracasan, 30% tienen un éxito moderado y un 10% tienen un gran éxito. Para mejorar sus posibilidades, el fabricante somete a una prueba sus nuevos productos, ante un grupo de clientes que actúa como jurado calificador. De los productos que fracasaron, 50% son calificados como malos, 30% como regulares y 20% como buenos. Para los que tuvieron un éxito moderado, la calificación es mala para un 20%, regular para un 40% y buena para otro 40%. Para los que tuvieron un gran éxito, los porcentajes son: malos 10%, regulares 30% y buenos 60%. El fabricante está interesado en conocer:

¿Cuál es la probabilidad conjunta de que un producto tenga un éxito moderado y reciba una mala calificación?
Si un nuevo producto tiene una buena calificación, ¿cuál es la probabilidad de que fracase?
¿Cuál es la probabilidad de que un producto tenga éxito moderado dado que este obtuvo una mala calificación?

Modelicemos el problema como una mixtura de distribuciones discretas según la Definición 1.20.

Sea $I_i$ la variable indicadora tal que

\[\begin{equation*} Pr(I = k) = \begin{cases} 0.25 & \text{ para } k = 1 \text{ fracaso}\\ 0.50 & \text{ para } k = 2 \text{ éxito moderado}\\ 0.25 & \text{ para } k = 3 \text{ gran éxito}. \end{cases} \end{equation*}\]

Luego definimos las variables $X_i$ que representan la calificación del jurado de un producto cuyo éxito o fracaso funcionó según $I=i$: $X_1$ calificación de un producto que fue un fracaso ($I=1$), $X_2$ calificación de un producto con un éxito moderado ($I=2$) y $X_3$ calificación de un producto con una gran éxito ($I=3$). Las distribuciones de $X_1, X_2, X_3$ vienen dadas por:

\[\begin{equation*} Pr(X_1 = k) = \begin{cases} 0.5 & \text{ para } k = 1 \text{ malo}\\ 0.3 & \text{ para } k = 2 \text{ regular}\\ 0.2 & \text{ para } k = 3 \text{ bueno}. \end{cases} \end{equation*}\]

\[\begin{equation*} Pr(X_2 = k) = \begin{cases} 0.2 & \text{ para } k = 1 \text{ malo}\\ 0.4 & \text{ para } k = 2 \text{ regular}\\ 0.4 & \text{ para } k = 3 \text{ bueno}. \end{cases} \end{equation*}\]

\[\begin{equation*} Pr(X_3 = k) = \begin{cases} 0.1 & \text{ para } k = 1 \text{ malo}\\ 0.3 & \text{ para } k = 2 \text{ regular}\\ 0.6 & \text{ para } k = 3 \text{ bueno}. \end{cases} \end{equation*}\]

Veamos el algoritmo de simulación necesario para este problema. Queremos simular productos que pueden haber tenido un gran éxito, un éxito moderado y o haber fracasado. Y para cada uno de ellos, queremos simular su calificación por el jurado que lo evaluó.

Consideramos una variable $I$ que indica el éxito de un nuevo producto y $X_I$ que indica la evaluación del producto por un jurado (para cada tipo de producto $I$). En esta situación debemos proporcionar las simulaciones correspondientes a $I$ e $X_I$. En concreto:

Paso 1. Establecer tamaño de muestra a simular $nsim$.

Repetir los pasos 2 y 3 para cada iteración $i$ de $1, 2,..., nsim$:

Paso 2. Simular de la variable indicador, $I_i$, mediante el algoritmo de la transformada inversa para una variable discreta con probabilidades $0.6, 0.3, 0.1$ (fracaso, éxito moderado, gran éxito), y seleccionar la variable $X_{I_i}$.
Paso 3. Simular un valor $x_{I_i}$ mediante el algoritmo de la transformada inversa para $X_i$ con valores malos, regulares, buenos, y probabilidades dadas por:
- fracasos (0.5, 0.3, 0.2)
- éxito moderado (0.2, 0.4, 0.4)
- gran éxito (0.1, 0.3, 0.6)
Paso 4. Devolver el conjunto de simulaciones $\{(I_i, x_{I_i})\}_{i=1}^{nsim}.$

Procedamos pues, a simular el proceso para, con las simulaciones, responder a las preguntas planteadas por la empresa.

# Parámetros iniciales
nsim <- 5000
semilla <- 12
# Descripción variable indicadora
exito <- c("Fracaso", "Moderado", "Éxito")
pexito <- c(0.6, 0.3, 0.1)
pexitoacum <- cumsum(pexito)
# Descripción del proceso de adquisión del microondas
clasifi <- c("Malo", "Regular", "Bueno")
p1 <- c(0.5, 0.3, 0.2)
p2 <- c(0.2, 0.4, 0.4)
p3 <- c(0.1, 0.3, 0.6)
p1acum <- cumsum(p1)
p2acum <- cumsum(p2)
p3acum <- cumsum(p3)

# Inicialización de variables para las simulaciones
producto <- c()             # éxito producto
jurado <- c()               # clasificación jurado

## Simulación del proceso
##########################
i <- 1
# Generamos uniformes para describir el proceso de indicadores de éxito
# y también el de evaluación o clasificación por el jurado
set.seed(semilla)
uexito <- runif(nsim)  
uclasi <- runif(nsim)

# Bucle de simulación
while (i <= nsim)
{
  # Éxito del producto
  producto[i] <- exito[min(which(uexito[i] <= pexitoacum))]
  # Tipo de microndas
  if(producto[i] == exito[1])
  {
    jurado[i] <- clasifi[min(which(uclasi[i] <= p1acum))]
  }
  else if (producto[i] == exito[2])
  {
    jurado[i] <- clasifi[min(which(uclasi[i] <= p2acum))]
  }
  else
  {
    jurado[i] <- clasifi[min(which(uclasi[i] <= p3acum))]    
  }
  # nueva simulación
  i <- i+1
}
# Resultado
simulacion <- data.frame(producto = producto, jurado = jurado)

A partir de las simulaciones, obtenemos la tabla conjunta de frecuencias (Tabla 1.1) y las frecuencias relativas (Tabla 1.2), que constituyen una aproximación de las probabilidades de ocurrencia.

distri.conjunta.frec <- table(simulacion)
kbl(distri.conjunta.frec,caption="Frecuencias observadas en las simulaciones.") %>%
  kable_styling(bootstrap_options = c("striped", "hover"),full_width = F)

Tabla 1.1: Frecuencias observadas en las simulaciones.
	Bueno	Malo	Regular
Éxito	327	47	166
Fracaso	650	1516	844
Moderado	616	292	542

distri.conjunta=as.data.frame(table(simulacion)/nsim)
kbl(distri.conjunta,caption="Frecuencias relativas observadas en las simulaciones. Aproximación de la distribución conjunta.") %>%
    kable_styling(bootstrap_options = c("striped", "hover"),full_width = F)

Tabla 1.2: Frecuencias relativas observadas en las simulaciones. Aproximación de la distribución conjunta.
producto	jurado	Freq
Éxito	Bueno	0.0654
Fracaso	Bueno	0.1300
Moderado	Bueno	0.1232
Éxito	Malo	0.0094
Fracaso	Malo	0.3032
Moderado	Malo	0.0584
Éxito	Regular	0.0332
Fracaso	Regular	0.1688
Moderado	Regular	0.1084

Podemos contestar ahora a las preguntas planteadas sin más que mirar la tabla anterior o realizar calculos sencillos con los datos obtenidos:

¿Cuál es la probabilidad conjunta de que un producto tenga un éxito moderado y reciba una mala calificación? Estamos interesados en la probabilidad

\[Pr(\text{Éxito = "Moderado" y Evaluación = "Malo"})\]

cuyo valor es 0.0584.

Si un nuevo producto tiene una buena calificación, ¿cuál es la probabilidad de que fracase? Para responder a esta pregunta podemos aplicar el Teorema de Bayes para resolver la probabilidad condicionada siguiente a partir de las frecuencias observadas en la simulación y mostradas en la Tabla 1.1,

\[Pr(\text{E= "Fracaso" | Eval= "Bueno"}) = \frac{Pr(\text{ E="Fracaso" , Eval= "Bueno"})}{Pr(\text{ Eval= "Bueno"})}\]

donde $E=$Éxito y $Eval=$Evaluación,

distri.conjunta.frec[2,1]/sum(distri.conjunta.frec[,1])

## [1] 0.4080352

o directamente seleccionar sobre la Tabla 1.2 las simulaciones en las que el producto fue evaluado como “Bueno” por el jurado, y contabilizar en cuántas de ellas el producto finalmente fracasó (a través del ratio correspondiente).

distri.conjunta %>% 
  filter(jurado == "Bueno") %>%
  mutate(pr.bueno = sum(Freq), resultado = round(Freq/pr.bueno,4)) %>%
  kbl(caption="Distribución condicionada a que el producto fue evaluado como Bueno por el jurado.")%>%
      kable_styling(bootstrap_options =c("striped","hoover"),full_width = F)

Tabla 1.3: Distribución condicionada a que el producto fue evaluado como Bueno por el jurado.
producto	jurado	Freq	pr.bueno	resultado
Éxito	Bueno	0.0654	0.3186	0.2053
Fracaso	Bueno	0.1300	0.3186	0.4080
Moderado	Bueno	0.1232	0.3186	0.3867

La probabilidad de interés resulta 0.4080. De hecho, en la Tabla 1.3 se muestran, en la columna “resultado,” las probabilidades condicionadas a que el jurado emitió una buena calificación del producto. ¿Cómo podemos interpretar esas probabilidades?

¿Cuál es la probabilidad de que un producto tenga éxito moderado dado que éste obtuvo una mala calificación? Procedemos como en la pregunta anterior ya que estamos interesados en

\[Pr(\text{E= "Moderado" | Eval = "Malo"}) = \frac{Pr(\text{E= "Moderado" , Eval = "Malo"})}{Pr(\text{ Eval= "Malo"})}\]

y lo resolvemos de nuevo generando la distribución condicionada a que la evaluación por el jurado sea “Mala,” que se muestra en la Tabla 1.4

distri.conjunta %>% 
  filter(jurado == "Malo") %>%
  mutate(pr.malo = sum(Freq), resultado = round(Freq/pr.malo,4)) %>%
  kbl(caption="Distribución condicionada a que el producto fue evaluado como Malo por el jurado.") %>%
  kable_styling(bootstrap_options =c("striped","hoover"),full_width = F)

Tabla 1.4: Distribución condicionada a que el producto fue evaluado como Malo por el jurado.
producto	jurado	Freq	pr.malo	resultado
Éxito	Malo	0.0094	0.371	0.0253
Fracaso	Malo	0.3032	0.371	0.8173
Moderado	Malo	0.0584	0.371	0.1574

La probabilidad de interés es 0.1574. ¿Cómo podemos interpretar la Tabla 1.4 de probabilidades obtenida?

1.7 Otras distribuciones continuas

En el caso de variables de tipo continuo de las que no disponemos de un generador de valores aleatorios pero sí disponemos de su función de densidad o distribución, podemos utilizar el algoritmo de la transformada inversa, dado en la definición 1.18, para obtener una muestra aleatoria de tamaño $n$ de su distribución.

En primer lugar estudiamos situaciones con una variable y posteriormente vemos ejemplos de sistemas de variables continuas o mixturas de discretas y continuas.

1.7.1 Una variable continua

Estudiamos aquí, a través de ejemplos, la simulación de variables aleatorias de tipo continua para las que conocemos la función de densidad o distribución, y se quiere revolver algún problema inferencial.

Ejemplo 1.16 Sea $X$ una variable aleatoria de tipo continuo cuya función de densidad viene dada por:

\[\begin{equation*} f(x) = 2e^{-2x} \text{ para } x \geq 0 \end{equation*}\]

Estamos interesados en conocer:

¿Cuál es la probabilidad de que la variable de interés tome valores en el intervalo [1, 2]?
¿Cuál es la probabilidad de que la variable de interés tome valores mayores o iguales a 1.5?
¿Cuál es el valor esperado de la variable? ¿y la desviación típica?

Para poder responder a las preguntas planteadas debemos obtener en primer lugar la función de distribución asociada a $X$, que viene dada por:

\[\begin{equation} F(x) = \int_0^x 2e^{-2s} ds=1 - e^{-2x} \text{ para } x \geq 0 \tag{1.22} \end{equation}\]

Podemos aplicar ahora el método de la transformada inversa para obtener una muestra de $X$.

El algoritmo de simulación basado en la transformada inversa, en la Definición 1.18 viene dado por:

Si $F(X)$ es la función de distribución para $X$ dada en la Ecuación (1.22)

Paso 1. Establecer el tamaño de muestra a simular $nsim$.

Repetir los pasos 2 y 3 para cada iteración $i$ de $1, 2,..., nsim$:

Paso 2. Generar $u_i$ a partir de una $U(0,1)$.
Paso 3. Aplicar el método de la transformada inversa para obtener $x_i = F^{-1}(u_i)$ con $F^{1}(u_i) = -log(1-u_i)/2.$
Paso 4. Devolver el conjunto de simulaciones $\{x_i\}_{i=1}^{nsim}$.

Apliquemos pues el algoritmo anterior, y generemos una muestra de tamaño $nsim=5000$ para $X$. Aprovechamos el calculo vectorial de R para no tener que hacer un bucle.

# Parámetros iniciales
nsim <- 5000
set.seed(12)
# Generamos uniformes 
uniforme <- runif(nsim)
# Calculamos x con F^-1
xs <- -log(1-uniforme)/2

Y con las simulaciones obtenidas, respondamos a cada una de las preguntas planteadas:

# Pr(1 <= X <= 2)
cat("Pr(1 <= X <= 2)=",round(mean(xs >= 1 & xs <= 2), 4))

## Pr(1 <= X <= 2)= 0.121

# Pr(X >= 1.5)
cat("Pr(X >= 1.5)=",round(mean(xs >= 1.5), 4))

## Pr(X >= 1.5)= 0.053

# Valor esperado y varianza
cat("E(X)=",round(mean(xs), 4))

## E(X)= 0.5046

cat("V(X)=",round(sd(xs), 4))

## V(X)= 0.5078

1.7.2 Transformaciones y Método de Composición

En ocasiones, se nos plantea el problema de inferir, a través de simulación, sobre una variable aleatoria $Y$ que se obtiene como una transformación continua de otra variable $X$ cuya distribución conocemos, esto es, \[Y=h(X), \quad \text{ con } X \sim F(x).\]

En particular, \[E(Y)=\int_S h(x) f(x)dx.\]

Se propone un algoritmo sencillo para simular muestras aleatorias de la variable $Y$, denominado método de composición y que se presenta a continuación.

Definición 1.21 Método de composición

Si $X$ es una variable aleatoria continua con función de distribución $F(X)$, e $Y$ otra variable aleatoria que se obtiene como $Y = h(X)$, donde $h()$ es una función continua, podemos obtener una muestra de $Y$ a partir del siguiente proceso:

Paso 1. Fijar el número de simulaciones ($nsim$).

Repetir los pasos 2 y 3 hasta alcanzar el número de simulaciones del paso 1.

Paso 2. Generar un valor de la variable $X$, $\{x_i \sim F(x)\}$.
Paso 3. Calcular el valor de la variable $Y$ para esa simulación mediante $y_i = h(x_i)$.
Paso 4. Devolver el conjunto de valores simulados $\{y_i\}_{i=1}^{nsim}.$

Ejemplo 1.17 Sea $X$ una variable aleatoria de tipo continuo cuya función de densidad viene dada por:

\[\begin{equation*} f(x) = 3x^2 \text{ para } 0 < x < 1 \end{equation*}\]

y consideramos la variable aleatoria $Y = 1 - X^2$. Estamos interesados en conocer:

¿Cuál es el valor esperado de la variable $Y$? ¿Y su desviación típica?
$Pr(Y \in [0,1])$
$Pr(Y \geq 0.5)$

Puesto que la distribución de $X$ no es de las estándar, para simular de ella hemos de utilizar el método de la transformada inversa (Definición 1.18), para lo que hemos de obtener necesariamente su función de distribución, que viene dada por:

\[\begin{equation} F(x) = \begin{cases} 0 & \text{ para } x <= 0\\ x^3 & \text{ para } 0 < x < 1\\ 1 & \text{ para } x \geq 1 \end{cases} \tag{1.23} \end{equation}\]

La función de distribución inversa es pues: \[F^{-1}(u)=u^{1/3}\]

El algoritmo para obtener una muestra de $Y$ viene dado por:

Si $F(X)$ es la función de distribución para $X$ dada en (1.23)

Paso 1. Establecer tamaño de muestra a simular $nsim$.

Repetir los pasos 2 a 4 para cada iteración $i$ de $1, 2,..., nsim$:

Paso 2. Generar $u_i$ a partir de una $U(0,1)$.
Paso 3. Aplicar el método de la transformada inversa para obtener $x_i = F^{-1}(u_i)=u^{1/3}$.
Paso 4. Actuar por composición y calcular $y_i = 1 - x_i^2$.
Paso 5. Devolver el conjunto $\{y_i\}_{i=1}^{nsim}.$

Procedemos con el algoritmo de simulación.

# Parámetros iniciales
nsim <- 5000
set.seed(12)
# Generamos uniformes 
uniforme <- runif(nsim)
# Calculamos x con F^-1
xs <- uniforme^(1/3)
# Calculamos y = h(x)
ys <- 1 - xs
# Devolvemos los valores de x e y
simulacion <- data.frame(sim = 1:nsim, x = xs, y = ys)

Podemos calcular ahora las cantidades de interés:

# Valor esperado y desviación típica de Y 
datos <- simulacion$y
cat("E(Y)=", round(mean(datos), 4))

## E(Y)= 0.2478

cat("sd(Y)=", round(sd(datos), 4))

## sd(Y)= 0.1915

# Pr(0 <= Y <= 1) 
cat("Pr(0 <= Y <= 1)=", round(sum(datos >= 0 & datos <= 1)/nsim, 4))

## Pr(0 <= Y <= 1)= 1

# Pr(Y >= 1) 
cat("Pr(Y >= 0.5)=", round(sum(datos >= 0.5)/nsim, 4))

## Pr(Y >= 0.5)= 0.121

Representamos gráficamente las simulaciones obtenidas tanto para la variable $X$ como la $Y$.

g1 <- ggplot(simulacion, aes(x, ..density..)) + 
  geom_histogram(fill = "steelblue") +
  geom_density()+
  labs(x = "X", y = "Densidad")
g2 <- ggplot(simulacion, aes(y, ..density..)) + 
  geom_histogram(fill = "steelblue") +
  geom_density()+
  labs(x = "Y", y = "Densidad")
grid.arrange(g1, g2, nrow = 1)

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.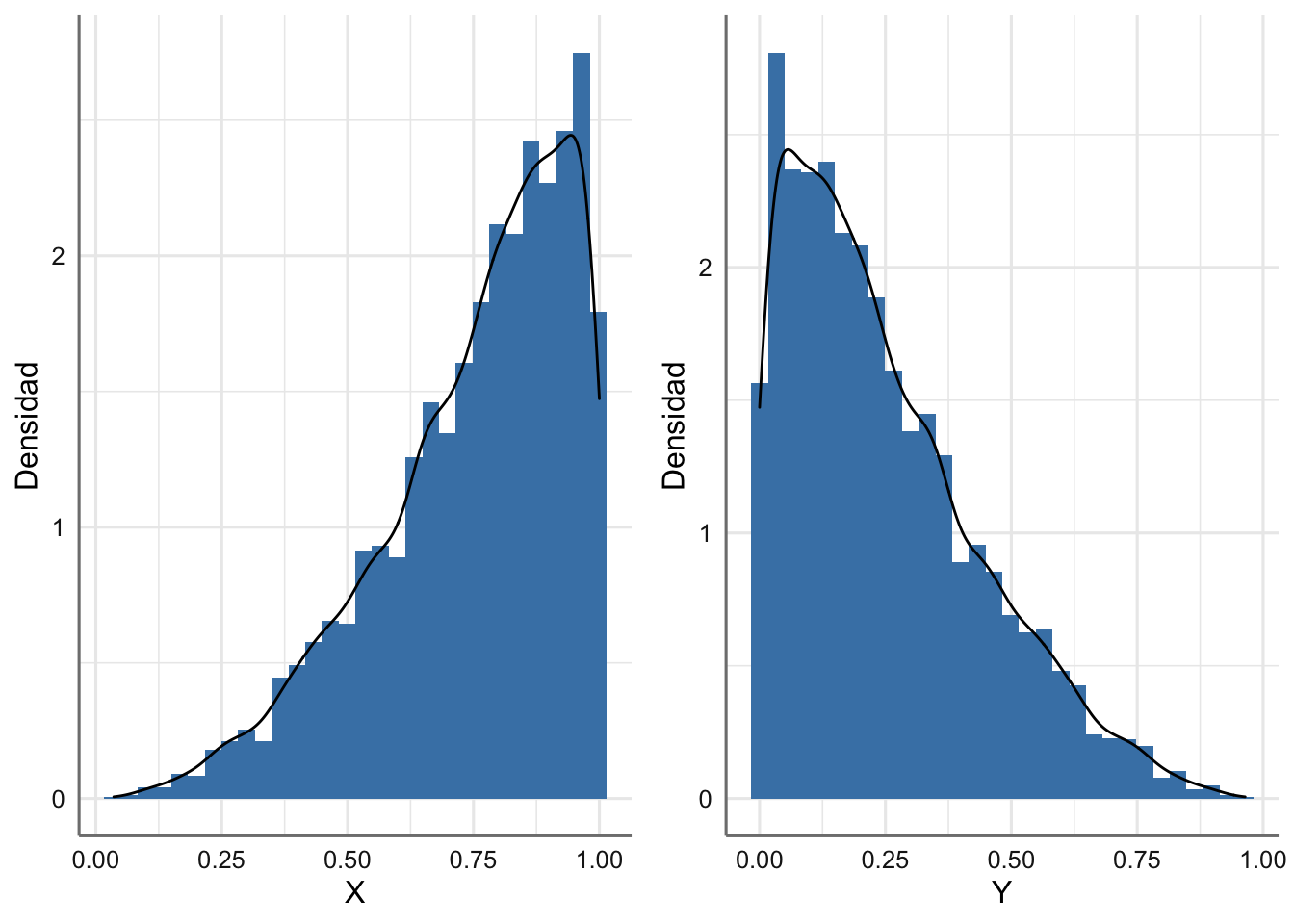

Figura 1.12: Función de densidad empírica e histogramas para X e Y.

1.7.3 Combinaciones de variables

Continuamos este bloque con un tipo de problema que nos encontraremos en muchas ocasiones en el análisis de sistemas, como es la definición de nuevas variables al operar (combinar aritméticamente) otras cuya distribución es conocida. Un ejemplo típico es la suma o resta de variables aleatorias. Imaginemos que tenemos dos variables $X_1$ y $X_2$ con funciones de densidad $f_1(x_1)$ y $f_2(x_2)$ respectivamente, y estamos interesados en estudiar las variables:

\[Y = X_1 + X_2 \quad\text{ y } \quad Z = X_1 - X_2\] Para el estudio de $Y$ y $Z$ podemos proceder teóricamente mediante los correspondientes cambios de variable, pero en situaciones má complejas o con más variables ese procedimiento es poco práctico. En dichas situaciones, podemos utilizar el método de composición para obtener una muestra de las nuevas variables.

Definición 1.22 Método de composición para combinaciones de variables

Si $X_1,..., X_n$ es un conjunto de variables aleatorias continuas con funciones de distribución $F_1,..., F_n$ y se define la variable aleatoria $Y$ mediante una transformación $h(X_1,...,X_n)$, donde $h()$ es una función continua, podemos obtener una muestra de $Y$ mediante el siguiente procedimiento:

Paso 1. Fijar el número de simulaciones ($nsim$).

Repetir pasos 2 y 3 hasta alcanzar el número de simulaciones fijado en el paso 1

Paso 2. Generar un valor de cada variable $X_i$, $x_{ji} \sim F(x_j), \quad j=1,\ldots,n$.
Paso 3. Calcular el valor de la variable $Y$ mediante $y_i = h(x_{1i},...,x_{ni})$.
Paso 4. Devolver el conjunto de valores simulados $\{y_i\}_{i=1}^{nsim}.$

Estudiamos a continuación algunos ejemplos donde se aplica el algoritmo expuesto.

Ejemplo 1.18 Supongamos que tenemos un conjunto de 10 variables $X_1,...,X_{10}$, tales que cada una de ellas se distribuye de forma independiente como: \[X_i \sim U(0,1), \quad i=1,...,10\] y consideramos además las variables aleatorias

\[\begin{eqnarray*} Y_{min} &=& min\{X_1,...,X_{10}\},\\ Y_{max} &=& max\{X_1,...,X_{10}\}. \end{eqnarray*}\]

Estamos interesados en conocer:

¿Cuál es el valor de $Pr[(Y_{min} \leq 0.1) \cap (Y_{max} \geq 0.8)]$.
¿Cuál es el valor esperado del rango, definido como $R = Y_{max} - Y_{min}$?
¿Cuál es el valor de $Pr(R \geq 0.5)$?

Auque el problema teórico se puede resolver fácilmente, vamos a plantear un algoritmo de simulación para responder a las cuestiones de interés.

Algoritmo para obtener una muestra de $Y_{min}, Y_{max}$ y $R$.

Paso 1. Fijar el número de simulaciones ($nsim$).

Repetir los pasos 2 a 4 hasta alcanzar el número de simulaciones fijado en el paso 1.

Paso 2. Generar valores $x_{1,i},...,x_{10,i} \sim U(0,1)$.
Paso 3. Aplicando composición calcular $y_{min,i} = min\{x_{1,i},...,x_{10,i}\}$ e $y_{max,i} = max\{x_{1,i},...,x_{10,i}\}$.
Paso 4. Aplicando composición calcular $r_{i} = y_{max,i} - y_{min,i}.$
Paso 5. Devolver el conjunto de valores simulados $\{y_{min,i}, y_{max,i}, r_{i}\}_{i=1}^{nsim}.$

Procedemos con el algoritmo de simulación. Aprovechamos las ventajas de R para el cálculo vectorial y evitar los bucles.

# Parámetros iniciales
nsim <- 5000
nvar <- 10  # número de variables
set.seed(12)
# Generamos matriz de datos uniformes de dimensiones nsim*nvar 
uniforme <- matrix(runif(nsim*nvar), nrow = nsim)
# Calculamos y_min e y_max
ymin <- apply(uniforme, 1, min)
ymax <- apply(uniforme, 1, max)
# Calculamos rango
rango <- ymax - ymin
# Devolvemos los valores 
simulacion <- data.frame(sim = 1:nsim, 
                         ymin = ymin, ymax = ymax, 
                         rango = rango)

Podemos evaluar ahora las cuestiones de interés a partir de la muestra obtenida para las tres variables.

#  Pr(Y_{min} <= 0.1, Y_{max} >= 0.8)$
p1 = mean((simulacion$ymin <= 0.1) & (simulacion$ymax >= 0.8))
cat("Pr(Y_{min} <= 0.1, Y_{max} >= 0.8)=", round(p1, 4))

## Pr(Y_{min} <= 0.1, Y_{max} >= 0.8)= 0.5732

# Valor esperado del rango 
cat("E(R)=",round(mean(simulacion$rango), 4))

## E(R)= 0.8183

# Pr(R >= 0.5)
cat("Pr(R >= 0.5)=",round(mean(simulacion$rango >= 0.5), 4))

## Pr(R >= 0.5)= 0.9874

Representamos en la Figura 1.13 la distribución obtenida a partir de las simulaciones para las tres variables consideradas.

orden <- c("ymin", "ymax", "rango")
# Construimos matriz de datos para el gráfico
datos <- pivot_longer(simulacion, cols = 2:4, 
                      names_to = "Medida", values_to = "Valor")
# gráfico
ggplot(datos, aes(Valor,fill = Medida))+
  geom_histogram(aes(y = ..density..), position = "identity", alpha = 0.3, bins = 50)+
  labs(y = "Densidad",x = "",fill = "Variables")

Figura 1.13: Simulaciones del mímimo, máximo y rango de X1,…,X10 v.a. U(9,1).

Ejemplo 1.19 En un estudio de calidad se está analizando el ajuste entre las pernos y las tuercas de cierto proceso de fabricación. Los pernos y las tuercas se fabrican de forma independiente y se colocan en dos cajas. Posteriormente se elige un perno y una tuerca y se prueba si encajan entre sí. Un perno y una tuerca ajustarán si el diámetro del agujero de la tuerca es mayor que el diámetro del perno y la diferencia entre estos diámetros no es mayor que 0.06 centímetros. Cuando no se cumplen estas especificaciones, tanto la tuerca como el perno se desechan. Las especificaciones de fabricación de los pernos indican que su diámetro se puede considerar que es una variable Normal con media 2 centimetros y desviación típica de 0.01 centímetros, mientras que el diámetro de las tuercas es una variable Normal con media 2.03 centímetros y desviación típica de 0.02 centímetros.

¿Cuál es la probabilidad de que encajen un perno y una tuerca elegidos al azar en una caja cualquiera?
Si se fabrican 10000 pernos y tuercas en un día, ¿cuántas desecharemos?
Si el porcentaje de desechos es inferior al 15% en un día no se modificarán las especificaciones de fabricación ¿Consideras que deberían modificarse las especificaciones de fabricación?

Partimos pues, para resolver el problema, de las variables $T\sim N(2.03, 0.02)$, que representa el diámetro de una tuerca, y $P \sim N(2, 0.01)$ que representa el diámetro de un perno. Las especificaciones de calidad exigen que $T>P$ y que $Dif=T-P\leq 0.6$, o lo que es lo mismo, $0<Dif\leq 0.6$.

Veamos cómo podríamos simular para responder a las preguntas planteadas.

Algoritmo para obtener la diferencia entre los diámetros de las tuercas y los pernos.

Paso 1. Fijar el número de simulaciones ($nsim$).

Repetir los pasos 2 a 4 hasta alacanzar el número de simulaciones fijado en el paso 1.

Paso 2. Generar valores $t_i\sim F(T)$ y $p_i \sim F(P)$ de sus respectivas distribuciones.
Paso 3. Aplicando composición, calcular $dif_i = t_i - p_i.$
Paso 4. Verificar el requisito de calidad: $0 < dif_i \leq 0.06$ y asignar $valid_i = 1$ si se cumple con el criterio y $valid_i = 0$ en otro caso.
Paso 5. Devolver el conjunto de valores simulados $\{t_i, p_i, dif_i, valid_i\}_{i=1}^{nsim}.$

Pongamos en práctica el algoritmo diseñado.

# Parámetros iniciales
nsim <- 5000
set.seed(12)
# Generamos diámetros para tuercas y pernos
tuercas <- rnorm(nsim, 2.03, 0.02)
pernos <- rnorm(nsim, 2.00, 0.01)
# Calculamos la diferencia y creamos filtro de calidad
diferencia <- tuercas - pernos
valid<- 1*(diferencia >0 & diferencia <= 0.06)
# Devolvemos los valores 
simulacion <- data.frame(sim = 1:nsim, 
                         tuercas = tuercas, 
                         pernos = pernos, 
                         diferencia= diferencia, 
                         valid = valid)

Representamos los datos simulados en la Figura 1.14, con la que podemos ya responder la primera pregunta:

¿Cuál es la probabilidad de que encajen un perno y una tuerca elegidos al azar en una caja cualquiera? Como vemos en la gráfica superior izquierda, la respuesta es 0.82, a la vista de que el 82% de las cajas inspeccionadas son válidas.

# Calidad del proceso
g1 <- simulacion %>%
  count(valid)%>%
  mutate(prop = prop.table(n)) %>%
  ggplot(aes(x = as.factor(valid), y = prop, label = scales::percent(prop))) + 
  geom_col(fill = "steelblue", position = "dodge") +
  scale_x_discrete(labels = c("No", "Sí")) +
  scale_y_continuous(labels = scales::percent)+
  geom_text(position = position_dodge(width = 0.9), vjust = 1.5,size = 3)+
  labs(x = "Resultado del proceso: validez", y = "Porcentaje")
# Diferencia
g2 <- ggplot(simulacion, aes(diferencia)) + 
  geom_histogram(fill = "steelblue",color="grey") +
  geom_vline(xintercept = c(0, 0.06), col = "red") +
  labs(x = "Diferencia Tuerca-Perno", y = "Frecuencia")
# Diámetros
orden <- c("tuercas", "pernos")
datos <- pivot_longer(simulacion, cols = 2:3, names_to = "Medida", values_to = "Valor")
# gráfico
g3 <- ggplot(datos, aes(Medida, Valor)) + 
  geom_boxplot(fill = "steelblue") +
  scale_x_discrete(limits = orden, labels = orden) +
  labs(x = "", y = "Diámetro")
# Combinación
grid.arrange(g1, g2, g3, nrow = 2)

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

Figura 1.14: Simulaciones del proceso de calidad para tuercas y pernos.

Respondemos las siguientes preguntas:

Si se fabrican 10000 pernos y tuercas en un día, ¿cuántas desecharemos? Si nuestra producción es de 10000 parejas, el número de parejas desechadas será igual a:

10000*(1 - mean(simulacion$valid == 1))

## [1] 1794

Si el porcentaje de desechos es inferior al 15% en un día no se modificarán las especificaciones de fabricación ¿Consideras que deberían modificarse las especificaciones de fabricación? Realmente el porcentaje de piezas desechadas es del 18% (gráfico superior izquierdo en la Figura 1.14), por lo que la recomendación sería abordar un proceso de mejora en la fabricación para reducir los defectos.

Ejemplo 1.20 Una empresa de fabricación de componentes para aviones tiene entre sus productos una barra que se coloca como sujeción en las alas, y que se construye mediante la unión consecutiva de tres secciones A, B, y C. Las especificaciones de fabricación establecen que la longitud (en pulgadas) de cada barra es una distribución Normal. Más concretamente la sección A tiene una media de 20 pulgadas y una varianza de 0.04. la longitud de la sección B tiene una media de 14 y varianza de 0.01, mientras que la sección C tiene una media de 26 y varianza 0.04. Las tres piezas se unen consecutivamente (A con B y B con C) de forma que se encajan superponiendo 2 pulgadas en cada unión. La barra sólo puede ser utilizada si su longitud total está entre 55.5 y 56.5 pulgadas.

¿Cuál es la probabilidad de que la barra sea utilizable?
Si en un mes se fabrican 25000 barras ¿cuál es el número de barras desechadas?
Por cada barra dentro de especificaciones se obtiene un beneficio de 300 euros, pero si se desecha, se genera una pérdida de 100 euros. ¿Cuál será el beneficio estimado en un mes?

Si denominamos $LA$, $LB$, y $LC$ a las variables aleatorias correspondientes a las longitudes de las secciones A, B, y C respectivamente, las distribuciones asociadas vienen dadas por:

\[LA \sim N(20, \sqrt{0.04}); \quad LB \sim N(14, \sqrt{0.01}); \quad LC \sim N(26, \sqrt{0.04})\]

La otra variable involucrada es la suma de barra al unir las piezas, que se obtiene como $L=LA+LB+LC-4$, dado que en cada junta se pierden 2 pulgadas. Las especificaciones de calidad sobre ella son $55.5 \leq L \leq y 56.5$.

Proponemos pues, un algoritmo de simulación que nos permita simular la longitud total de la barra a partir de cada una de las secciones, y verificar si está dentro de las especificaciones de calidad establecidas.

Paso 1. Fijar el número de simulaciones ($nsim$).

Repetir los pasos 2 a 4 hasta alcanzar el número de simulaciones fijado en el paso 1.

Paso 2. Generar valores $LA_i$, $LB_i$, y $LC_i$ a partir de sus distribuciones correspondientes.
Paso 3. Aplicando composición, calcular $L_i = LA_i + LB_i + LC_i - 4.$
Paso 4. Verificar el requisito de calidad: $55.5 \leq L_i \leq 56.5$ y asignar $valid_i = 1$ si lo cumple, y $valid_i = 0$ si no lo cumple.
Paso 5. Devolver el conjunto de valores simulados $\{LA_i, LB_i, LC_i, L_i, valid_i\}_{i=1}^{nsim}.$

Programemos el algoritmo.

# Parámetros iniciales
nsim <- 5000
set.seed(12)
# Generamos longitudes de las secciones
LA <- rnorm(nsim, 20, sqrt(0.04))
LB <- rnorm(nsim, 14, sqrt(0.01))
LC <- rnorm(nsim, 26, sqrt(0.04))
# Calculamos longitud total y verificamos requisitos
L <- LA + LB + LC - 4
valid <- 1*(L >= 55.5 & L <= 56.5)
# Devolvemos los valores 
simulacion <- data.frame(sim = 1:nsim, LA = LA, LB = LB, 
                         LC = LC, L = L,valid=valid)

Respondamos a las preguntas a partir de las simulaciones obtenidas.

¿Cuál es la probabilidad de que la barra sea utilizable? La respuesta viene aproximada por la proporción de piezas válidas. Calculamos también un intervalo de confianza utilizando la ecuación (1.5).

#  Pr proceso cumpla criterios calidad
p = mean(simulacion$valid == 1)
error = sqrt((sum(simulacion$valid-p)^2)/(nsim^2))
alpha = 0.05 # 1-alpha=nivel de confianza para el IC
ic.low = p - qnorm(1-alpha/2)*error
ic.up = p + qnorm(1-alpha/2)*error
cat("Pr(barra utilizable)=", p)

## Pr(barra utilizable)= 0.9016

cat("Error de la aproximación=", error)

## Error de la aproximación= 4.298784e-17

cat("IC(", 1-alpha,"%)= [", ic.low,",", ic.up,"]")

## IC( 0.95 %)= [ 0.9016 , 0.9016 ]

Dado el error tan pequeño que genera el proceso de simulación, la estimación proporcionada es claramente precisa.

Si en un mes se fabrican 25000 barras ¿cuál es el número de barras desechadas?

desechos=25000*(1-p)
cat("Barras desechadas en un mes:", desechos)

## Barras desechadas en un mes: 2460

Por cada barra dentro de especificaciones se obtiene un beneficio de 300 euros, pero si se desecha, se genera una pérdida de 100 euros. ¿Cuál será el beneficio estimado en un mes?

benef=(25000-desechos)*300-desechos*100
cat("Beneficio obtenido en un mes:", benef, "€")

## Beneficio obtenido en un mes: 6516000 €

1.7.4 Modelos secuenciales

En la última sección para variables de tipo continuo presentamos los primeros modelos de simulación para variables aleatorias que actúan de forma consecutiva a lo largo del tiempo. Será pues, una introducción a los modelos estocásticos que estudiaremos en el resto de unidades. En estas situaciones todas las variables involucradas en el sistema hacen referencia al tiempo de ocurrencia de los eventos de interés. Trabajemos con ejemplos, para entender los conceptos y problemas involucrados.

Ejemplo 1.21 El equipo de mantenimiento de una empresa debe programar las visitas a cierta instalación para establecer una calendario eficiente de revisiones. El sistema que debe analizar está compuesto por tres procesos (A, B, y C) que funcionan de forma independiente, pero que están conectados en serie, de forma que todo el sistema se detiene si un proceso falla. El tiempo de vida o tiempo hasta un fallo o avería, medido en horas, para cada uno de los procesos se puede considerar aleatorio y responde a distribuciones exponenciales con medias 1000, 333, y 167 respectivamente.

El proceso de fabricación completo, que involucra a los tres procesos A, B y C, funciona 24 horas al día y completa un ciclo cada siete días, tras el cual realiza un parón para tareas de mantenimiento. En ese ciclo, los procesos A, B y C operan consecutivamente durante un día: $A$ trabaja durante 15.6 horas, luego entra en funcionamiento el proceso $B$ durante 5.52 horas, y finalmente el $C$ durante 2.88 horas.

En la actualidad el equipo de manteniento está interesado en reajustar el ciclo para realizar las labores de mantenimiento, si fuera necesario, y reducir el tiempo muerto en que el sistema está parado, pues en estos momentos se dedican 24 horas tras cada ciclo, para las tareas de mantenimiento.

¿Cuál es la probabilidad de que el sistema falle antes de finalizar un ciclo de trabajo?
¿Cuál de los procesos está generando más parones en el ciclo debidos a una avería?
¿Cuál es el tiempo medio de funcionamiento del sistema sin ningún fallo? Interesa además, un rango o intervalo de confianza para dicha estimación. ¿Cuál sería el tiempo óptimo del ciclo para abordar las tareas de mantenimiento?

En primer lugar modelicemos el sistema en base a la información proporcionada. Definamos las variables aleatorias $TA$, $TB$, y $TC$ que representan, respectivamente, el tiempo de funcionamiento -o tiempo a fallo- (en horas) de cada proceso A, B y C. Sus distribuciones son: \[TA \sim Exp(1/1000); \quad TB \sim Exp(1/333); \quad TC \sim Exp(1/167).\] También son importantes las siguientes cantidades: - El tiempo de funcionamiento requerido cada día para cada uno de los procesos $ta=15.6, tb=5.52, tc=2.88$ y el número de días que conforma cada ciclo, $nciclo=7$.

El tiempo de vida potencial del sistema completo, esto es, el tiempo $T$ que funciona el sistema de fabricación hasta un fallo, y que se calcula a partir del mínimo número de días que funciona cada proceso, $min \{TA/ta,TB/tb,TC/tb\}$.

Propongamos pues, un algoritmo de simulación que reproduzca el proceso de fabricación para un número $nsim$ de ciclos simulados, cuyas simulaciones permitan responder a las preguntas planteadas.

Algoritmo para el estudio de fallo del sistema

Paso 1. Fijar el número de simulaciones o ciclos a simular ($nsim$).

Repetir los pasos 2 a 4 tantas veces como simulaciones a generar (nsim).

Paso 2. Generar valores $TA_i$, $TB_i$, y $TC_i$ de los tiempos a fallo de cada proceso según su distribución.
Paso 3. Calcular el número de días que dura sin fallos cada proceso, con los ratios $rt_i=\{TA_i/ta, TB_i/tb, TC_i/tc\}$. Identificar cuál falla primero ($min(rt_i)$).
Paso 4. Verificar si el primero en fallar lo hace antes de terminar el ciclo, $min(rt_i)<=7$. Si es que sí, guardar cuál es el proceso responsable del fallo y calcular la duración del ciclo mediante $24*rt_i$ horas. Si es que no, indicarlo y especificar como duración del ciclo $24*7$ horas.
Paso 5. Devolver los valores de las simulaciones de los tiempos a fallo de cada proceso, de la duración del ciclo, el indicador de fallo y el proceso responsable en cada ciclo (simulación).

# Función para simular el proceso de fabricación con tres subprocesos ABC encadenados.
simula.proceso=function(nsim, nciclo, alpha, beta, delta, ta, tb, tc){
# semilla=Semilla aleatoria y nsim=nº simulaciones o ciclos a simular
#nciclo es el número de días del ciclo
# alpha, beta y delta son los parámetros de las exponenciales TA,TB,TC
# ta,tb y tc son los tiempos de funcionamiento diarios para los procesos A, B y C.
Tciclo=Dciclo = rep(0, nsim)   # tiempo de ciclo (en horas T y días D)
Tpotencial = rep(0, nsim)      # tiempo(en horas) que funcionaría sin fallos
fallo = c()                   # qué proceso ha fallado en cada ciclo
procesos = c("A", "B", "C")

# simulamos las duraciones para todos los ciclos
TA = rexp(nsim, alpha)  
TB = rexp(nsim, beta)
TC = rexp(nsim, delta)
t = c(ta, tb, tc) # funcionamiento diario de cada proceso

for(j in 1:nsim){
  T = c(TA[j], TB[j], TC[j])      # tiempos de vida para el ciclo j
  nfallo = T/t                  # número días que funcionará cada proceso
  falla = which.min(nfallo)     # qué proceso falla primero
  if(nfallo[falla] <= nciclo){  # si falla antes de cerrar el ciclo
   fallo[j] = procesos[falla]   #identificamos el proceso que falla
   Dciclo[j] = T[falla]/t[falla]   # y lo pasamos a días
   Tciclo[j] = Tpotencial[j]=24*Dciclo[j]   # duración del ciclo (en horas)
  }
  else{                       #si no falla ninguno antes de cerrar el ciclo
    Tciclo[j] = 24*7            #cerramos el ciclo sin fallos
    Dciclo[j] = 7
    fallo[j] = "No"
    Tpotencial[j] = T[falla]/t[falla]*24    # y guardamos la duración potencial 
  }
} # fin del for (j)
resultado = data.frame(ciclo = 1:nsim, fallo,
                     Tciclo = round(Tciclo, 2),Dciclo = round(Dciclo, 2),
                     Tpotencial = round(Tpotencial, 2),
                     DA = round(TA/ta, 2), DB = round(TB/tb, 2), DC = round(TC/tc, 2))

return(resultado)
}

Lanzamos el proceso para los valores del ejemplo, y visualizamos los resultados en la Tabla 1.5

nciclo = 7; alpha = 1/1000; beta = 1/333; delta = 1/167
ta = 15.6;tb = 5.52; tc = 2.88
semilla = 12

set.seed(semilla)
nsim=5000                  
simulacion=simula.proceso(nsim,nciclo,alpha,beta,delta,ta,tb,tc)
kbl(head(simulacion),caption="Simulaciones para el proceso de fabricación con tres subprocesos encadenados A, B y C. Tipo de fallo, tiempos de funcionamiento del sistema (Tciclo en horas, Dciclo en días) y tiempo de funcionamiento potencial (Tpotencial en horas). Días de vida DA, DB, DC de los procesos.") %>%
 kable_styling(bootstrap_options = "striped", full_width = F, position = "left")

Tabla 1.5: Simulaciones para el proceso de fabricación con tres subprocesos encadenados A, B y C. Tipo de fallo, tiempos de funcionamiento del sistema (Tciclo en horas, Dciclo en días) y tiempo de funcionamiento potencial (Tpotencial en horas). Días de vida DA, DB, DC de los procesos.
ciclo	fallo	Tciclo	Dciclo	Tpotencial	DA	DB	DC
1	No	168.00	7.00	219.46	140.33	9.14	59.78
2	No	168.00	7.00	171.59	40.74	7.15	18.27
3	C	96.63	4.03	96.63	7.52	32.32	4.03
4	B	34.45	1.44	34.45	183.16	1.44	259.42
5	No	168.00	7.00	617.69	116.45	87.16	25.74
6	No	168.00	7.00	435.89	18.16	83.25	112.44

¿Cuál es la probabilidad de que el sistema falle antes de finalizar un ciclo de trabajo?

m = mean(simulacion$fallo != "No")
error = sqrt(sum(((simulacion$fallo != "No")*1-m)^2) / (nsim^2))
ic.low = m - qnorm(0.975)*error
ic.up = m + qnorm(0.975)*error
cat("Pr(fallo antes del ciclo=",m)

## Pr(fallo antes del ciclo= 0.2876

cat("IC(Probabilidad)=[",round(ic.low, 4),",",round(ic.up, 4),"]")

## IC(Probabilidad)=[ 0.2751 , 0.3001 ]

¿Cuál de los procesos está generando más parones en el ciclo debidos a una avería?

En la Figura 1.15 representamos (a la izquierda) el porcentaje que se detiene el proceso de fabricación antes de finalizar el ciclo, para cada uno de los tipos de fallo posible (debido a un parón en A, B o C), y difieren muy poco entre sí. El más frecuente, dentro de la similaridad es el fallo en el proceso C, con una probabilidad de 0.0986. A la derecha de la gráfica vemos cómo los tres tipos de fallo están dando tiempos de fabricación muy similares en media y variabilidad.

#  Representación gráfica del ciclo de vida: tabla de probabilidades
g1 = simulacion %>%
  group_by(fallo) %>%
  summarise(n = n(), prop = n/nrow(simulacion)) %>%
  ggplot(aes(x = fallo, y = prop)) +
    geom_col(aes(fill = fallo), position = "dodge") +
    geom_text(aes(label = scales::percent(prop), 
                  y = prop, group = fallo),
              position = position_dodge(width = 0.9),
              vjust = 1.5)+
  labs(x = "Tipo de fallo",y = "Proporción")+
  theme(legend.position = "none")


# Tiempo de vida en función del ciclo
g2 <- ggplot(simulacion, aes(fallo, Tciclo)) + 
  geom_boxplot(fill = "steelblue") +
  labs(x = "Tipo de fallo", y = "Tiempo de funcionamiento (horas)")
grid.arrange(g1, g2, nrow = 1)

Figura 1.15: Gráfico del ciclo de vida y de la probabilidad del tiempo de fabricación sin fallos.

¿Cuál es el tiempo medio de funcionamiento del sistema sin ningún fallo? Interesa además, un rango o intervalo de confianza para dicha estimación. ¿Cuál sería el tiempo óptimo del ciclo para abordar las tareas de mantenimiento?

Respondemos esta pregunta utilizando no el tiempo de ciclo impuesto como cota superior, sino el tiempo de funcionamiento que el sistema es capaz de aguantar sin fallos, recogido en la variable Tpotencial(en horas). Damos una estimación y construimos un intervalo de confianza al 95% para responder la pregunta.

m = mean(simulacion$Tpotencial)
error = sqrt(sum((simulacion$Tpotencial-m)^2) / (nsim^2))
ic.low = m - qnorm(0.975)*error
ic.up = m + qnorm(0.975)*error
cat("E(Tpotencial)=",round(m/24, 2))

## E(Tpotencial)= 20.54

cat("IC(estimación)=[",round(ic.low/24, 2),",",round(ic.up/24, 2),"]")

## IC(estimación)=[ 19.98 , 21.11 ]

Resulta pues, que el sistema de fabricación tiene capacidad para funcionar sin fallos una media de 20.5 días, y el intervalo de confianza da un límite inferior de 19.98, lo que da justificaría, con unas garantías del 97.5%, reajustar el ciclo y darle un tamaño de 20 días, reduciendo así considerablemente los parones de un día completo de mantenimiento cada 7 en funcionamiento.

Ejemplo 1.22 El gerente de una empresa que se dedica a la extracción y venta de piedra natural está preocupado porque piensa que hay un problema con la máquina que se dedica a cortar, en bloques más manejables, los bloques de piedra que vienen desde la cantera. La máquina trabaja durante 24 horas al día los 365 días del año, y las especificaciones de calidad establecen que la media y varianza del tiempo hasta que la máquina se detiene por un fallo, $TF$, han de ser de 80 y 50 horas respectivamente.

En el histórico de mantenimiento de la empresa se han detectado tres tipos de fallos que se han catalogado como leves, moderados y graves. Además, la información del equipo de mantenimiento indica que el tipo de fallo que se produce está muy relacionado con el tiempo de funcionamiento de la máquina, de forma que la probabilidad de que se produzca un fallo u otro varía de acuerdo a la tabla siguiente:

TF vs Fallo	Leve	Moderado	Grave
$TF \leq 1500$	0.85	0.10	0.05
$1500 < TF \leq 3000$	0.75	0.15	0.10
$TF > 3000$	0.65	0.20	0.15

Los tiempos de reparación (medidos en minutos), $TR$, tienen medias y varianzas dadas por:

Fallo	Media	Varianza
Leve	30	15
Moderado	60	30
Grave	120	45

Además se sabe que si el fallo es leve, no es necesario detener la producción por completo, ya que esta se puede reducir al 60% y seguir trabajando mientras se realiza la reparación. En los otros dos casos la máquina debe detenerse por completo.

El gerente está interesado en conocer el funcionamiento de la máquina en los próximos seis meses asumiendo que las variables de tiempo de funcionamiento y tiempo de reparación son de tipo Weibull. En concreto desea saber qué porcentaje del tiempo la máquina estará trabajando a pleno rendimiento, a rendimiento reducido y parada.

Antes de plantear un algoritmo de simulación, tratemos de entender y modelizar bien la secuenciación de variables involucradas, según las especificaciones dadas. Las variables descritas son:

$TF$: Tiempo de funcionamiento de la máquina hasta fallo.
$averia$: Tipo de avería cuando el sistema falla: leve, moderado, grave. Su distribución depende de $tf$.
$TR.xx$: Tiempo de reparación para una avería “xx={leve, moderado, grave},” que depende del tipo de avería.

El tiempo de funcionamiento a pleno rendimiento vendrá dado por el tiempo acumulado en el que el sistema funciona sin ningún fallo, obtenido de todos los $TF$ simulados. El funcionamiento a rendimiento reducido se dará mientras se está reparando alguna avería de tipo leve. El tiempo de parada del sistema corresponde a los periodos en los que se está reparando alguna avería de tipo moderada o grave. Puesto que el funcionamiento del sistema depende del tipo de avería, nos interesará guardar información sobre el tipo de avería que se está reparando, información que recopilaremos en la variable $averia$. El tiempo dedicado a reparaciones lo guardaremos en una variable global denominada $TREPARA$, que nos permitirá calcular cuándo el sistema no funciona a pleno rendimiento.

$TREPARA$: Tiempo total dedicado a reparaciones.

En cada simulación nos interesará contabilizar el tiempo transcurrido, en una variable

$ciclo$: Tiempo de funcionamiento hasta fallo + tiempo de reparación.

Interesa simular el funcionamiento del sistema en los próximos seis meses, de modo que dicho periodo expresado en minutos es de 2.592^{5}, y la simulación parará cuando $ttotal<259200$ minutos, siendo

$ttotal$: tiempo total acumulado de funcionamiento y reparaciones.

Puesto que nos piden modelizar con distribuciones Weibull y sólo nos han dado su media y su varianza, hemos de calcular los parámetros a utilizar, para lo que acudimos a la función que ya propusimos en la Ecuación (1.19).

# Parámetros tiempo funcionamiento (en minutos)
tf.params <- estima.weibull(80*60, 50*60); tf.params

## [1]    1.64 5365.22

# Tiempo de reparación para avería leve
tr.leve <- estima.weibull(30, 15); tr.leve

## [1]  2.10 33.87

# Tiempo de reparación para avería moderada
tr.moderado <- estima.weibull(60, 30); tr.moderado

## [1]  2.10 67.74

# Tiempo de reparación para avería moderada
tr.grave <- estima.weibull(120, 45); tr.grave

## [1]   2.90 134.58

Así, tendremos las siguientes distribuciones para el tiempo de funcionamiento $tf$ y los tiempos de reparación $tr$:

\[\begin{eqnarray*} TF &\sim& Weib(1.64,5365.22) \\ TR.leve &\sim& Weib(2.10, 33.87) \\ TR.moderado &\sim& Weib(2.10, 67.74) \\ TR.grave &\sim& Weib(2.90, 134.58). \end{eqnarray*}\]

Veamos ahora el algoritmo de simulación para este problema.

Algoritmo secuencial para el estudio de fallo de la máquina

Paso 1. Inicializar todos las variables temporales a 0.

Repetir los pasos 2 a 5 hasta que $tiempo > 6*30*24*60 = 259200$ minutos.

Paso 2. Generar $tf$.
Paso 3. Generar el tipo de averia $averia$ en función de $tf$.
Paso 4. Generar el tiempo de reparación $trepara$ en función del tipo de avería.
Paso 5. Actualizar el tiempo total acumulado $ttotal$ con el tiempo de funcionamiento y reparación.
Paso 6. Devolver el conjunto de valores simulados.

# Fijamos semilla y límite de tiempo para la simulación
semilla <- 12
set.seed(semilla)
Tsim <- 259200
# Incicializamos variables
tf <- c()
trepara <- c()
averia <- c()
ttotal <- 0
ciclo <- c(0)
# Creamos variables necesarias para la simulación del tipo de avería:
# probabilidades de avería leve, moderada y grave
eti <- c("leve", "moderada", "grave")
pr1 <- c(0.85, 0.10, 0.05)  # si tf<=1500
pr1acu <- cumsum(pr1)
pr2 <- c(0.75, 0.15, 0.10)  # si 1500<tf<=3000
pr2acu <- cumsum(pr2)
pr3 <- c(0.65, 0.20, 0.15)  # si tf>3000
pr3acu <- cumsum(pr3)

#############################
## Simulación del proceso
#############################
i <- 1
while (ttotal<= Tsim)
{
  # Tiempo de funcionamiento
  tf[i] <- rweibull(1, tf.params[1], tf.params[2])
  # Tipo Averia
  if(tf[i] <= 1500)
      averia[i] <-eti[min(which(runif(1) <= pr1acu))]
  else if(tf[i] > 1500 & tf[i] <= 3000)
      averia[i] <-eti[min(which(runif(1) <= pr2acu))] 
  else if(tf[i] > 3000)
       averia[i] <-eti[min(which(runif(1) <= pr3acu))]
 # tiempo de reparación
  if(averia[i] == "leve")
      trepara[i] <- rweibull(1, tr.leve[1], tr.leve[2])
  else if(averia[i] == "moderada" )
      trepara[i] <- rweibull(1, tr.moderado[1], tr.moderado[2])
  else if(averia[i] == "grave")
      trepara[i] <- rweibull(1, tr.grave[1], tr.grave[2]) 
  # actualizamos tiempo total
  ciclo[i]=tf[i]+trepara[i]
  ttotal=ttotal+ciclo[i]
  i <- i + 1
}
simulacion <- data.frame(tf, averia = as.factor(averia), 
                         trepara,tiempo = cumsum(ciclo))

Mostramos en la Tabla 1.6 las simulaciones obtenidas y damos a continuación una breve descripción.

kbl(head(simulacion),caption = "Simulaciones para el sistema de corte de piedra.") %>%
  kable_classic_2(full_width = F)

Tabla 1.6: Simulaciones para el sistema de corte de piedra.
tf	averia	trepara	tiempo
9761.123	moderada	17.61378	9778.737
6330.278	leve	60.52762	16169.542
7472.127	leve	63.77925	23705.449
13942.609	leve	15.95977	37664.017
5291.304	leve	38.77331	42994.094
4762.548	leve	26.86817	47783.511

# Descriptivo del sistema
summary(simulacion)

##        tf               averia      trepara            tiempo      
##  Min.   :  532.4   grave   : 5   Min.   :  5.171   Min.   :  9779  
##  1st Qu.: 2460.9   leve    :41   1st Qu.: 21.329   1st Qu.: 84710  
##  Median : 3878.1   moderada: 9   Median : 33.343   Median :146116  
##  Mean   : 4687.1                 Mean   : 43.292   Mean   :142494  
##  3rd Qu.: 6600.7                 3rd Qu.: 59.206   3rd Qu.:204825  
##  Max.   :13942.6                 Max.   :159.389   Max.   :260174

Respondamos ya a diversas preguntas de interés.

¿Cuál es tiempo total de funcionamiento del sistema, incluidas reparaciones?
¿Qué porcentaje del tiempo total el sistema ha estado a pleno rendimiento, reducido y en parada?

# Tiempo total de funcionamiento del sistema (con reparaciones)
ttotal <- last(simulacion$tiempo)
# Tiempo a pleno rendimiento
tpleno <- sum(simulacion$tf)
# Tiempo a rendimiento reducido
tparcial <-sum((simulacion$averia == "leve")*trepara*0.6)
# Tiempo parado (reparaciones moderadas y graves)
tdetenido <- sum((simulacion$averia != "leve")*trepara)
# Juntamos los tiempos y calculamos porcentajes sobre el tiempo de funcionamiento total
kbl(round(100*cbind(ttotal, tpleno, tparcial, tdetenido)/ttotal,2),
    col.names=c("%Tiempo total","%Pleno rendimiento","%Rendimiento reducido","%Parado")) %>%
  kable_classic_2(full_width = F)

%Tiempo total	%Pleno rendimiento	%Rendimiento reducido	%Parado
100	99.08	0.3	0.42

Se concluye que el 99.08% del tiempo durante los seis meses simulados, el sistema ha estado a pleno rendimiento, operando sin averías.

1.8 Procesos estocásticos

Una vez hemos recordado cuestiones básicas y distribuciones comunes de probabilidad, a la vez que hemos aprendido algunos algoritmos como el de la Transformada Inversa (Sección 1.5 o el de Composición Sección 1.7.2), damos un paso más y presentamos el concepto de procesos estocásticos, que es el objeto de esta asignatura.

Definición 1.23 Un proceso estocástico es una secuencia de variables aleatorias $\{X(t), t \in T\}$ y que dependen del parámetro $t$, que toma valores en el conjunto índice $T$ o de instantes de tiempo.

Se denomina espacio de estados del proceso, $S$, al conjunto de todos los posibles valores de las variables aleatorias que componen el proceso.

Si $T$ es un conjunto de tiempos discretos, $t = 0, 1, 2, 3,...$, definidos por ejemplo al finalizar cada día o cada hora, obtenemos un proceso estocástico de tiempo discreto (PETD), $\{X(0), X(1), X(2),...\}$.

En cambio, si observamos el sistema continuamente a lo largo del tiempo $t>\geq 0$, obtenemos un proceso estocástico de tiempo continuo (PETC), $\{X(t), t \geq 0\}$.

El espacio de estados de un proceso puede ser de tipo discreto o continuo, en función de los posibles valores que pueden tomar las variables aleatorias $X(t)$ que lo componen.

1.8.1 Ejemplos de procesos estocásticos

A continuación veamos algunos ejemplos de procesos PETD y PETC. Te proponemos identificar en cada uno de ellos cuáles pueden ser las cuestiones de interés a investigar.

En primer lugar, presentamos algunos ejemplos de procesos estocásticos de tiempo discreto (PETD).

Ejemplo 1.23 Sea $X_t$ la temperatura (en grados centígrados) registrada en el aeropuerto de Alicante-Elche a las 12:00 horas del día $t$. El espacio de estados del proceso estocástico $S$ viene dado por $(-20, 50).$ Esto implica que la temperatura nunca baja de veinte bajo cero ni supera los cincuenta grados; da lugar a un espacio de estados continuo.

Ejemplo 1.24 Consideramos como $X_t$ la variable aleatoria que registra el número ganador de la ONCE en el sorteo diario. Puesto que los números tienen 5 dígitos, el espacio de estados es discreto y viene dado por el conjunto de enteros entre 00000 y 99999.

Ejemplo 1.25 Sea $X_t$ la variable aleatoria que registra el valor del IPC al final del mes $t$ para España. En tería el IPC puede tomar cualquier valor ente $(-\infty, +\infty)$, por lo que el espacio de estados es continuo.

Ejemplo 1.26 Sea $X_t$ el número de reclamaciones que recibe una compañía de seguros una semana cualquiera $t$. El espacio de estados es discreto y viene dado por $\{0, 1, 2, 3, 4,...\}$.

Ejemplo 1.27 Sea $X_t$ el número de accidentes que ocurren en la carretera que une las poblaciones de Elche y Santa Pola en la semana $t$. El espacio de estados es discreto y viene dado por $\{0, 1, 2, 3, 4,...\}$.

Ejemplo 1.28 Sea $X_t$ el número de productos defectuosos que genera una cadena de producción en cada uno de los lotes fabricados a lo largo de un día. El espacio de estados es discreto, $\{0, 1, 2, 3, 4,...\}$ y también $t$, que identifica el número de lote producido.

Y a continuación veamos otros ejemplos de procesos estocásticos de tiempo continuo (PETC).

Ejemplo 1.29 Supongamos que una máquina puede estar en dos estados, encendido o apagado. Sea $X(t)$ la variable aleatoria que refleja el estado de la máquina en el instante de tiempo $t$. Entonces $\{X(t), t \geq 0\}$ es un proceso estocástico de tiempo continuo con el espacio de estados discreto, con valores posibles {encendido, apagado}.

Ejemplo 1.30 Un ordenador personal (PC) puede ejecutar muchos procesos simultáneamente. Si $X(t)$ es el número de procesos que se ejecutan en dicho PC en el momento $t$. Entonces $X(t), t \geq 0$ es un proceso estocástico de tiempo continuo con espacio de estados discreto $0, 1, 2,...,K$ ,donde $K$ es el número máximo de trabajos que puede manejar el PC simultáneamente.

Ejemplo 1.31 Sea $X(t)$ es el número de clientes que entran a una tienda de libros en una franja de tiempo de duración $t$. Entonces $X(t), t \geq 0$ es un proceso estocástico de tiempo continuo con espacio de estados discreto $0, 1, 2,...$.

Ejemplo 1.32 Sea $X(t)$ una variable que recopila información sobre si se produce o no un fallo en el sistema de alimentación eléctrico de un circuito a lo largo del tiempo. El espacio de estados es discreto, con valores $\{0,1\}$.

Ejemplo 1.33 Sea $X(t)$ la temperatura en grados centígrados registrada en una localización dada en cualquier instante de tiempo $t$. Entonces $X(t), t \geq 0$ es un proceso estocástico de tiempo continuo con espacio de estados continuo.

1.8.2 Función de distribución del proceso

Los ejemplos anteriores muestran una variedad de problemas que pueden ser modelados y estudiados como procesos estocásticos, y para hacerlo será preciso analizar el comportamiento aleatorio del proceso, sea cual sea la naturaleza de los tiempos, discretos o continuos.

Puesto un proceso estocástico es una colección de variables aleatorias, la forma de inferir sobre él es a través de la función de distribución conjunta que se construye a partir de las variables $X(t_1), X(t_2),...,X(t_n)$:

\[\begin{equation} F(x_1, x_2,...,x_n) = Pr(X(t_1) \leq x_1, X(t_2) \leq x_2,..., X(t_n) \leq x_n) \tag{1.24} \end{equation}\]

donde $x_1, x_2,..., x_n \in \mathbb{R}^n.$

Si el proceso estocástico tiene una estructura simple, entonces los cálculos no son excesivamente complicados, pero no suele ser la tónica de procesos útiles para representar sistemas reales. A lo largo de los años los investigadores han modelizado y estudiado clases especiales de procesos estocásticos que pueden utilizarse para describir una gran variedad de sistemas reales, resolviendo y posibilitando así los cálculos probabilísticos necesarios, aunque su complejidad en ocasiones no haya sido evitable. Las dos clases más importantes de procesos estocásticos ya modelizados son las cadenas de Markov de tiempo discreto (CMTD) y las cadenas de Markov de tiempo continuo (CMTC). Sin embargo, en los últimos años el desarrollo de la computación ha posibilitado el uso intensivo de la simulación para resolver de un modo sencillo cálculos probabilísticos complejos y así analizar fácilmente el comportamiento de los sistemas reales, sin necesidad de extraer analíticamente la distribución de probabilidad conjunta del proceso.

En los temas siguientes iremos describiendo este tipo de procesos, mostrando los resultados teórico, pero centrándonos en cómo utilizar las herramientas de simulación disponibles para reproducir el comportamiento del sistemas reales sin necesidad de registrar datos ni de realizar complejos desarrollos probabilísticos.

Por analogía con el análisis de variables aleatorias serán relevantes en el estudio de procesos estocásticos, su valor esperado, $E[X(t)]$, su varianza, $V[X(t)] = E[X(t)^2] - E[X(t)]^2$ y la covarianza $Cov[X(t), X(s)] = E[X(t)X(s)] - E[X(t)]E[X(s)]$, que vendrán dadas en función de tiempos $t$ y $s$.

1.9 Ejercicios

1.9.1 Básicos

Ejercicio B1.1. Un proceso de fabricación tiene una tasa de defectos del 20% y los artículos se colocan en cajas de cinco. Un inspector toma muestras de dos artículos de cada caja. Si uno o los dos artículos seleccionados son defectuosos, la caja se rechaza. Si un cliente pide 10 cajas, ¿cuál es el número esperado de artículos defectuosos que recibirá el cliente? Da una aproximación del error y una banda de confianza.

Ejercicio B1.2. Un vendedor a domicilio vende ollas y sartenes. Sólo entra en el 50% de las casas que visita. De las casas en las que entra, 1/6 de los propietarios no están interesados en comprar nada, 1/2 de ellos acaban haciendo un pedido de 60 dólares, y 1/3 de ellos acaban haciendo un pedido de 100 dólares. Estima el promedio de ventas (en dólares) conseguidas para 25 visitas (junto con una medida del error). Estima el promedio de ventas por visita.

Ejercicio B1.3. Un contratista de techos independiente ha determinado que el número de trabajos que se solicitan para el mes de septiembre es bastante variable. A partir de la experiencia anterior, las probabilidades de obtener 0, 1, 2 o 3 trabajos se han determinado como 0.1, 0.35, 0.30 y 0.25, respectivamente. El beneficio obtenido por cada trabajo es de 300 dólares. ¿Cuál es el beneficio esperado para el mes de septiembre?

Ejercicio B1.4. Un sistema de visión está diseñado para medir el ángulo en el que el brazo de un robot se desvía de la vertical. Sin embargo, el sistema de visión no es totalmente preciso, y el resultado de las observaciones es una variable aleatoria con una distribución uniforme. Si la medición indica que el rango del ángulo está entre 9.7 y 10.5 grados, aproxima por simulación la probabilidad de que el ángulo real esté entre 9.9 y 10.1 grados y da una medida del error de dicha aproximación.

Ejercicio B1.5. En una operación de soldadura automatizada, la posición en la que se coloca la soldadura es muy importante. La desviación del centro de la placa es una variable aleatoria normal con una media de 0 pulgadas y una desviación estándar de 0.01 pulgadas. Una desviación positiva indica una desviación a la derecha del centro y una desviación negativa indica una desviación a la izquierda del centro.

¿Cuál es la probabilidad de que en una placa dada, la ubicación real de la soldadura se desvíe menos de 0.005 pulgadas (en valor absoluto) del centro?
¿Cuál es la probabilidad de que en una placa dada, la ubicación real de la soldadura se desvíe más de 0.02 pulgadas (en valor absoluto) del centro?

Da aproximaciones del error cometido al aproximar por simulación.

Ejercicio B1.6. Un departamento de compras percibe que el 75% de sus pedidos especiales se reciben a tiempo. De los pedidos que se reciben a tiempo, el 80% cumple totalmente las especificaciones; de los pedidos que llegan con retraso, el 60% cumple con las especificaciones. Responde a las siguientes preguntas utilizando simulación, dando también una medida del error.

¿Cuál es la probabilidad de que un pedido llegue a tiempo y cumpla con las especificaciones?
¿Cuál es la probabilidad de que un pedido cumpla con las especificaciones?
Si se han recibido cuatro pedidos, ¿cuál es la probabilidad de que los cuatro pedidos cumplan con las especificaciones?

Ejercicio B1.7. Una empresa manufacturera tiene tres operarios para una máquina que produce cierto tipo de componentes. El operario A tiene una tasa de defectos del 5%, el operario B del 3%, y el operario C del 2%. Los tres operarios producen el mismo número de componentes. Si un componente elegido al azar resulta defectuoso, ¿cuál es la probabilidad de que el componente haya sido producido por A, B, o C? Responde a la pregunta con simulación y da una medida del error de la aproximación.

Ejercicio B1.8. El 1% de los préstamos que hace cierta empresa financiera no son saldados (es decir, la cantidad prestada no le es devuelta en su totalidad). La compañía efectúa un estudio rutinario de las posibilidades crediticias de los solicitantes. Encuentra que el 30% de los préstamos no saldados se hicieron a clientes de alto riesgo, el 40% a clientes de riesgo moderado y el restante 30% a clientes de bajo riesgo. De los préstamos que fueron saldados, el 10% se hicieron a clientes de alto riesgo, el 40% a clientes de riesgo moderado y el 50% a clientes de bajo riesgo. Responde a las siguientes preguntas utilizando simulación, dando también una medida del error.

¿Cuál es la probabilidad de que un préstamo de alto riesgo no sea saldado?
¿Cuál es la probabilidad de que una deuda no saldada, dado que el riesgo es moderado?

Ejercicio B1.9. Se hacen dos inversiones de 10000€ cada una en dos proyectos. Se supone que el proyecto A va a producir un rendimiento neto de 800, 1000 y 1200 euros con probabilidades respectivas de 0.2, 0.6, 0.2. Se supone que el proyecto B va a producir una ganancia neta de 800, 1000, y 1200 euros, con probabilidades respectivas 0.3, 0.4, 0.3. Si asumimos que lo que se gana con un proyecto es independiente de lo que se gana con el otro, responde a las siguientes preguntas utilizando simulación, dando también una medida del error.

¿Cuál es la probabilidad de que la ganancia total sea de 2000 euros exactamente?
¿Cuál es la probabilidad de que la ganancia total sea igual o superior a 2000 euros?
¿Cuál es la probabilidad de que la ganancia sea inferior a 2000 euros?

Ejercicio B1.10. Sea $X$ una variable aleatoria de tipo continuo cuya función de densidad viene dada por:

\[\begin{equation*} f(x) = \frac{5}{3}(1-x^3)x \text{ para } 0 \leq x \leq 1 \end{equation*}\]

Utilizando simulación:

Determina la $Pr(X \leq 0.5).$
Determina la $Pr(0.25 \leq X \leq 0.75).$
Determina la $Pr(X > 1/3).$

Ejercicio B1.11. Sea $X$ una variable aleatoria de tipo continuo cuya función de densidad viene dada por:

\[\begin{equation*} f(x) = \frac{1}{8}x \text{ para } 0 \leq x \leq 4 \end{equation*}\]

Utilizando simulación:

Determina el valor de $t$ tal que $Pr(X \leq t) = 0.25$
Determina el valor de $t$ tal que $Pr(X \leq t) = 0.5$

Ejercicio B1.12. Sea $X$ una variable aleatoria de tipo continuo cuya función de densidad viene dada por:

\[\begin{equation*} f(x) = e^{-x} \text{ para } x > 0 \end{equation*}\]

Utilizando simulación:

Determina el valor esperado y la desviación típica de la variable $Y = X^{1/2}.$
Determina $Pr(Y \geq 1).$

Ejercicio B1.13. Los administradores de cierta industria han probado, por pruebas técnicas, que su producto tiene una vida media de 5 años, y la han descrito con una distribución exponencial. Si el tiempo de garantía asignado por los administradores es de 1 año, ¿qué porcentaje de sus productos será devuelto para reparar durante el periodo de garantía? Aproxima por simulación y da una medida del error.

1.9.2 Avanzados

Ejercicio A1.1.

Los problemas de inventario tratan de dar respuesta a las necesidades de almacenamiento de las empresas para satisfacer la demanda de los consumidores. En concreto, en este caso se plantea el problema de un distribuidor del mercado central especializado en la venta de fresas. Dicho comerciante compra cajas al precio de 20€, y las vende por 50€, y tiene dos problemas relacionados directamente con lo que denominamos “inventario”:

Si los clientes solicitan más cajas de las disponibles el comerciante pierde 30€ por cada caja de menos disponible.
Si el comerciante almacena más cajas de las solicitadas por los clientes, el producto se debe tirar y pierde 20€ por cada caja que no vende.

Para tratar de determinar el número de cajas que debe comprar y almacenar, recoge información sobre la demanda realizada por los clientes en la campaña anterior, cuyos datos vienen dados en la tabla siguiente:

Cajas Vendidas	10	11	12	13
Número de días	15	20	40	25

La empresa proporciona en la tabla siguiente las ganancias esperadas diarias (en euros) asociadas al número de cajas vendidas y las cajas que debería almacenar:

Demanda	10	11	12	13
Almacenar 10	300	300	300	300
Almacenar 11	280	330	330	330

En base a esta información se debe obtener la ganancia esperada para cada acción de inventario, y determinar aquella que proporcione mayores beneficios, es decir, las mayores ganancias diarias. ¿Qué recomendación se debería hacer al distribuidor?

Por otro lado, los asesores convencen al distribuidor de que para tener mayor certeza de sus ganancias debería realizar un estudio marginal, que se basa en el hecho de que cuando se compra una unidad adicional de un artículo (en este caso una caja) pueden ocurrir dos cosas: la unidad se vende o no se vende. De esta forma:

¿Cuál es la probabilidad de que la demanda sea al menos de 11 cajas? ¿Y de al menos 12? ¿Y de al menos 13?
¿Cuál resulta la ganancia y pérdida marginal esperada por la venta o no de una caja más con cada una de las probabilidades anteriores?
¿Qué opción recomiendas al distribuidor?

Software

2 Cadenas de Markov de Tiempo Discreto

TF vs Fallo	Leve	Moderado	Grave
\(TF \leq 1500\)	0.85	0.10	0.05
\(1500 < TF \leq 3000\)	0.75	0.15	0.10
\(TF > 3000\)	0.65	0.20	0.15